Hai tam giác bằng nhau và các trường hợp bằng nhau của hai tam giác – Toán lớp 7
Với cách giải Các dạng bài tập về Hai góc đối đỉnh môn Toán lớp 7 Hình học gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập Hai tam giác bằng nhau và các trường hợp bằng nhau của hai tam giác. Mời các bạn đón xem:
Hai tam giác bằng nhau và các trường hợp bằng nhau của hai tam giác - Toán lớp 7
I. LÝ THUYẾT:
1. Hai tam giác bằng nhau:
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
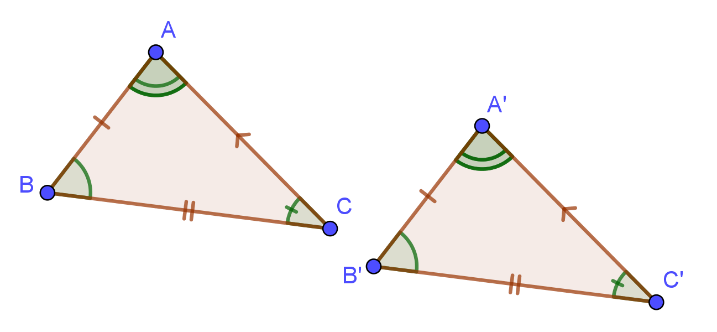
Hai tam giác ABC và A'B'C' bằng nhau ta viết
nếu
2. Các trường hợp bằng nhau của hai tam giác thường:
a. Trường hợp bằng nhau thứ nhất của hai tam giác: cạnh - cạnh - cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
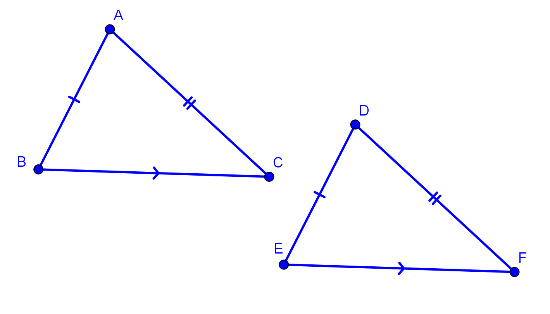
Hai tam giác ABC và DEF có: thì (c.c.c)
b. Trường hợp bằng nhau thứ hai của hai tam giác: cạnh - góc - cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
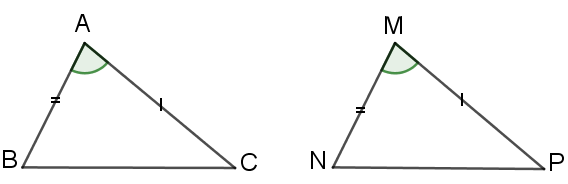
Hai tam giác ABC và MNP có:
thì (c.g.c)
*Hệ quả: Nếu hai cạnh góc vuông của hai tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thi hai tam giác vuông đó bằng nhau.
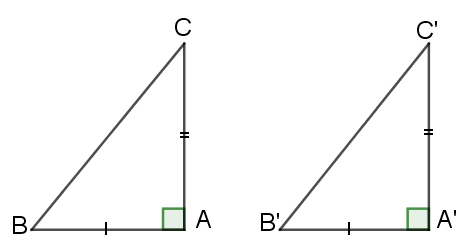
c. Trường hợp bằng nhau thứ ba của hai tam giác: cạnh - góc - cạnh (g.c.g)
Nếu một cạnh và hai góc kề của tam giác này bằng một góc và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
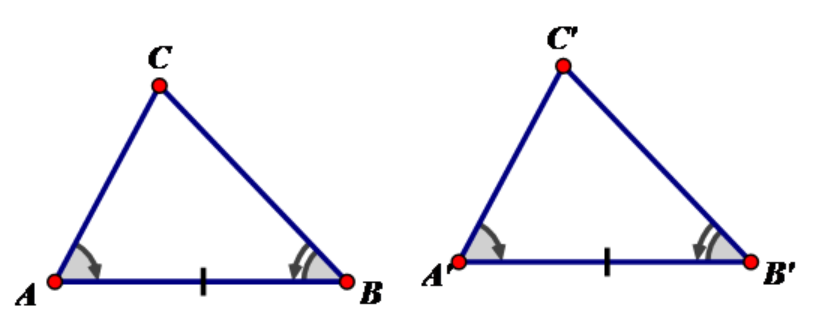
Hai tam giác ABC và A'B'C' có:
Thì (g.c.g)
Hệ quả 1: Nếu một cạnh góc vuông và góc nhọn kề với cạnh ấy của tam giác vuông này bằng cạnh góc vuông và góc nhọn kề với cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau.
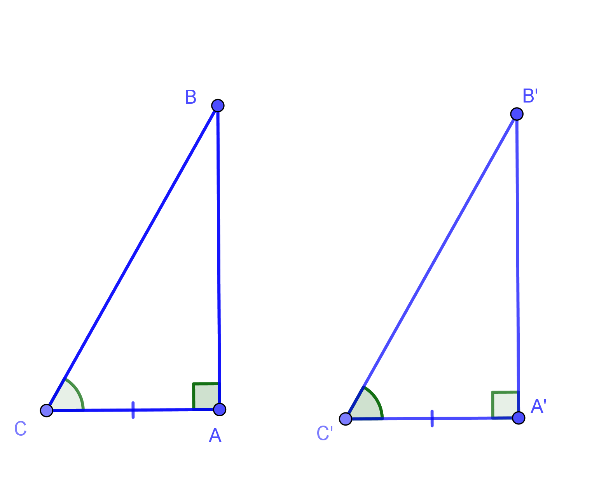
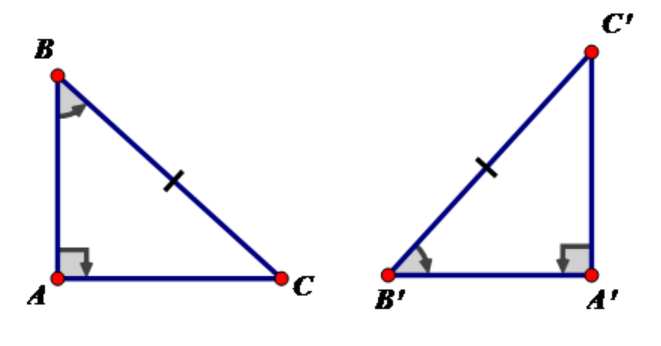
Hệ quả 2: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
II. CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 2.1: Dựa vào hai tam giác bằng nhau để tính độ dài đoạn thẳng, tính số đo góc, chứng minh hai cạnh, hai góc bằng nhau.
1. Phương pháp giải:
Từ hai tam giác bằng nhau, suy ra các cạnh, các góc tương ứng bằng nhau.
Chú ý: Căn cứ vào quy ước viết các đỉnh tương ứng của hai tam giác bằng nhau theo đúng thứ tự, ta viết được các góc bằng nhau, các đoạn thẳng bằng nhau.
2. Ví dụ minh họa:
Ví dụ 1: Cho . Tính số đo các góc còn lại của tam giác MNP và độ dài cạnh NP.
Giải:
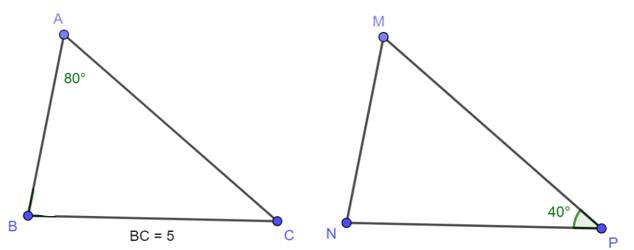
Ta có
Theo định nghĩa hai tam giác bằng nhau:
BC = NP = 5cm
Áp dụng định lý tổng ba góc trong tam giác MNP có:
Vậy NP = 5cm.
Dạng 2.2: Vẽ tam giác khi biết độ dài ba cạnh, biết hai cạnh và một góc xen giữa hoặc một cạnh và hai góc kề.
1. Phương pháp giải:
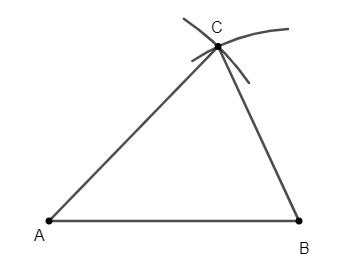
*Vẽ tam giác ABC biết độ dài ba cạnh:
- Vẽ một trong ba đoạn thẳng cho trước, ta chọn đoạn thẳng AB.
- Vẽ cung tròn tâm A bán kính AC
- Vẽ cung tròn tâm B bán kính BC.
- Hai cung tròn này cắt nhau tại C.
- Nối CA, CB, ta được tam giác ABC cần vẽ.
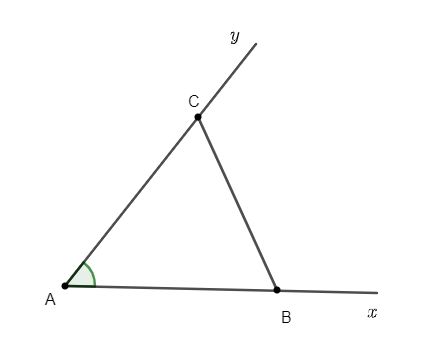
*Vẽ tam giác ABC biết độ dài hai cạnh AB, AC và góc BAC xen giữa:
- Vẽ .
- Xác định điểm B thuộc tia Ax có độ dài AB cho trước.
- Xác định điểm C thuộc tia Ay có độ dài AC cho trước.
- Vẽ đoạn thẳng BC, ta được tam giác ABC cần vẽ.
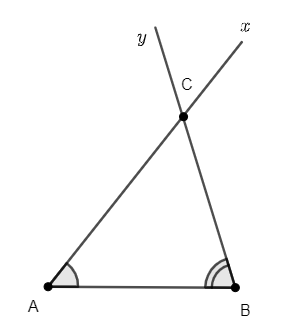
*Vẽ tam giác ABC biết độ dài cạnh AB và hai góc kề là góc BAC và ABC:
- Vẽ đoạn thẳng AB.
- Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By sao cho
- Hai tia Ax và By cắt nhau tại C.
- Ta được tam giác ABC cần vẽ.
2. Ví dụ minh họa:
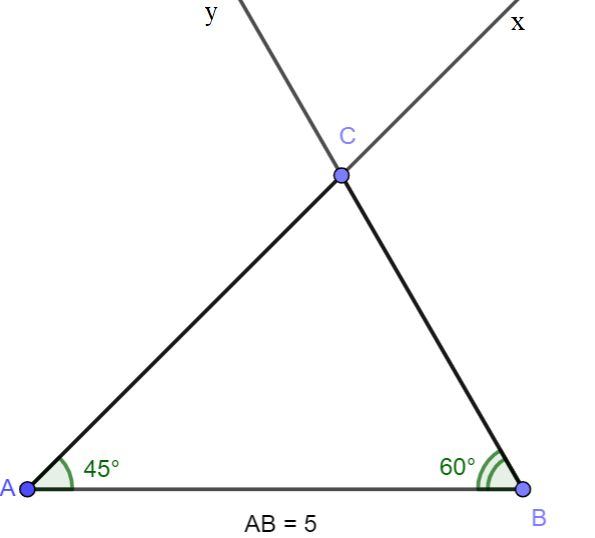
Ví dụ 2: Vẽ tam giác ABC biết AB = 5cm,
Giải:
- Vẽ đoạn thẳng AB = 5cm.
- Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By sao cho
- Hai tia Ax và By cắt nhau tại C.
- Ta được tam giác ABC cần vẽ.
Dạng 2.3: Chứng minh hai tam giác bằng nhau theo trường hợp thứ nhất, thứ hai, thứ ba.
1. Phương pháp giải:
- Xét hai tam giác.
- Kiểm tra ba điều kiện bằng nhau: cạnh - cạnh - cạnh, cạnh - góc - cạnh hoặc góc -cạnh - góc.
- Kết luận hai tam giác bằng nhau.
2. Ví dụ minh họa:
Ví dụ 3: Cho có . Chứng minh: bằng hai cách.
Giải:
Cách 1:
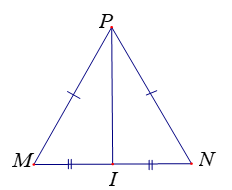
Lấy I là trung điểm của MN, nối I với P.
* Xét hai tam giác và có:
MI = NI (I là trung điểm của MN)
cạnh IP chung
PM = PN (gt)
Do đó: = (c.c.c)
(2 góc tương ứng bằng nhau) hay (đpcm).
Cách 2:
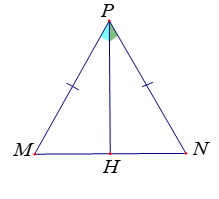
Kẻ tia phân giác PH của góc cắt MN tại H.
* Xét hai tam giác và có:
PM = PN (gt)
(PH là tia phân giác của góc )
cạnh PH chung
Do đó: = (c.g.c)
(2 góc tương ứng bằng nhau) hay (đpcm).
Ví dụ 4: Cho hình vẽ, biết OP = OQ và PE // FQ, hãy chứng minh
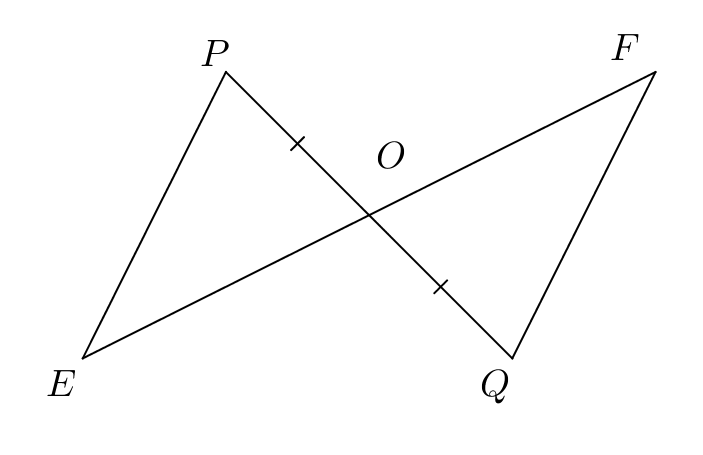
Giải:
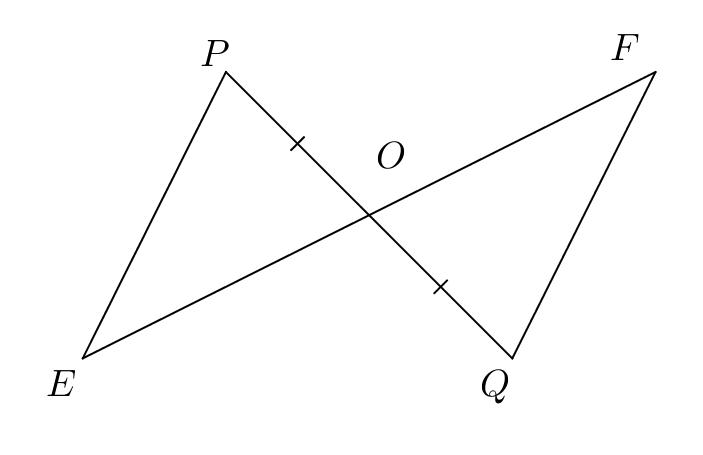
|
GT |
Cho OP = OQ, PE // FQ |
|
KL |
|
Vì PE // FQ nên (hai góc so le trong)
Xét và có:
(cmt)
OP = OQ (gt)
(hai góc đối đỉnh)
Nên
III. BÀI TẬP VẬN DỤNG:
Bài 1: Cho . Biết . Số đo góc A’B’C’ là:
A. 60o
B. 70o
C. 80o
D. 90o
Bài 2: Cho hình vẽ sau, khoanh tròn vào các đáp án đúng:
vì có:
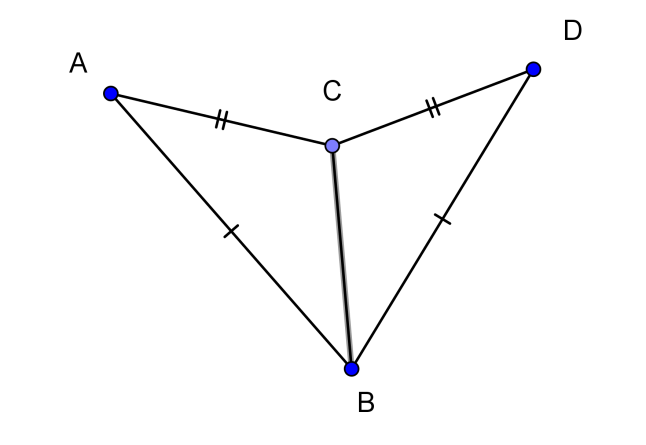
A. Cạnh chung BD.
B. BD = CA.
C. Cạnh chung BC.
D. CD = CA.
E. BD = BA.
F. CD = BA.
Bài 3: Cho hình vẽ:

a) Cần có thêm điều kiện gì để ?
b) Cho . Biết . Em có thể tính góc nào của tam giác BFD?
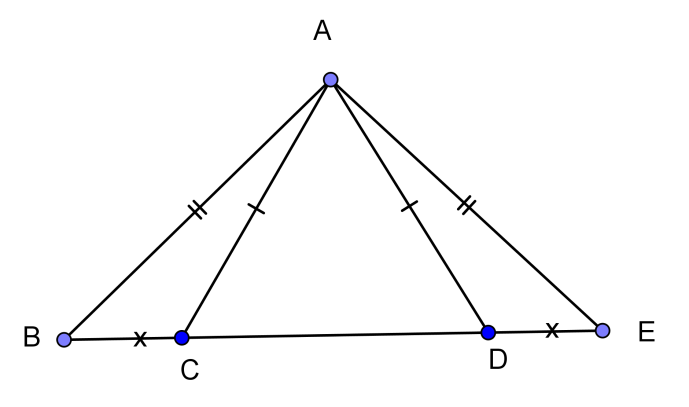
Bài 4: Cho hình vẽ sau, tìm tất cả các cặp tam giác bằng nhau và chứng minh.
Bài 5: Cho tam giác ABC có AC = BC, D là trung điểm của AB. Biết . Tính số đo .
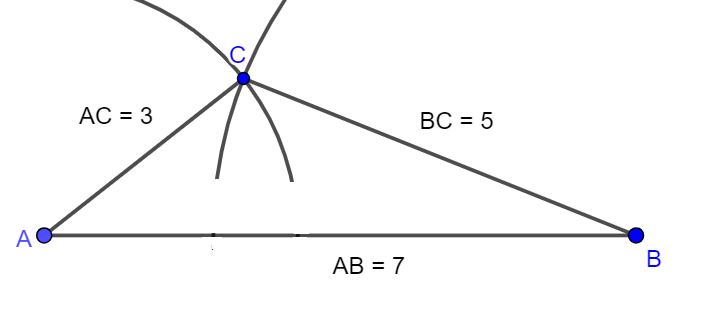
Bài 6: Vẽ tam giác ABC biết AB = 7cm, BC = 5cm, CA = 3cm.
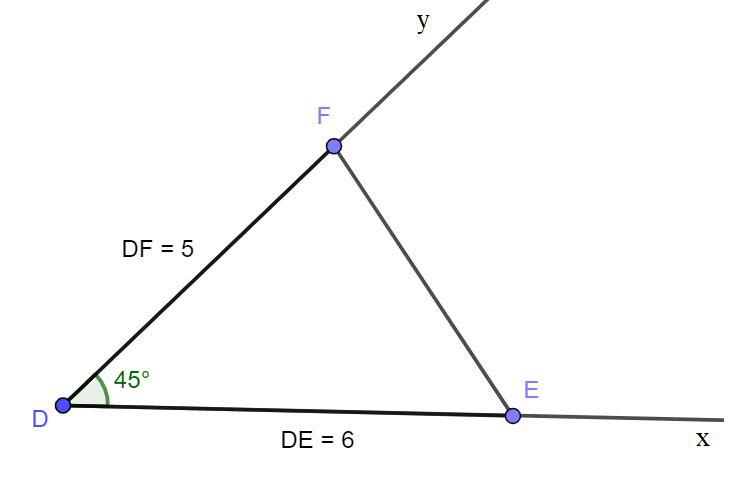
Bài 7: Vẽ tam giác DEF biết DE = 6cm, DF = 5cm,
Bài 8: Cho tam giác ABC vuông tại A có đường phân giác AI của tam giác (I nằm trên BC), biết góc ngoài tại đỉnh C là 150o. Tính góc
Bài 9: Cho và . Tính tỉ số diện tích của tam giác EFM và diện tích tam giác KPN.
Bài 10: Cho tam giác ABC có , tia phân giác BD của góc B . Trên cạnh BC lấy điểm E sao cho BE = BA.
a) Chứng minh rằng = ;
b) Chứng minh BD là trung trực của AE.
Hướng dẫn giải:
Bài 1: Đáp án A.
Bài 2: Đáp án C, D, E.
Bài 3:
a) AC = BD
b)
Bài 4:
Bài 5:
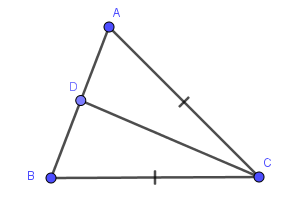
Xét và có:
AC = BC (gt)
AD = BD (vì D là trung điểm của AB)
Cạnh CD chung
Nên
(hai góc tương ứng)
Do đó
Bài 6:
Cách vẽ:
- Vẽ đoạn thẳng AB = 7cm.
- Vẽ cung tròn tâm A bán kính 3cm.
- Vẽ cung tròn tâm B bán kính 5cm.
- Hai cung tròn này cắt nhau tại C.
- Nối CA, CB ta được tam giác ABC cần vẽ.
Bài 7:
Cách vẽ:
- Vẽ
- Trên tia Dx lấy điểm E sao cho DE = 6cm.
- Trên tia Dy lấy điểm F sao cho DF = 5cm.
- Nối E với F ta được tam giác DEF cần vẽ.
Bài 8:
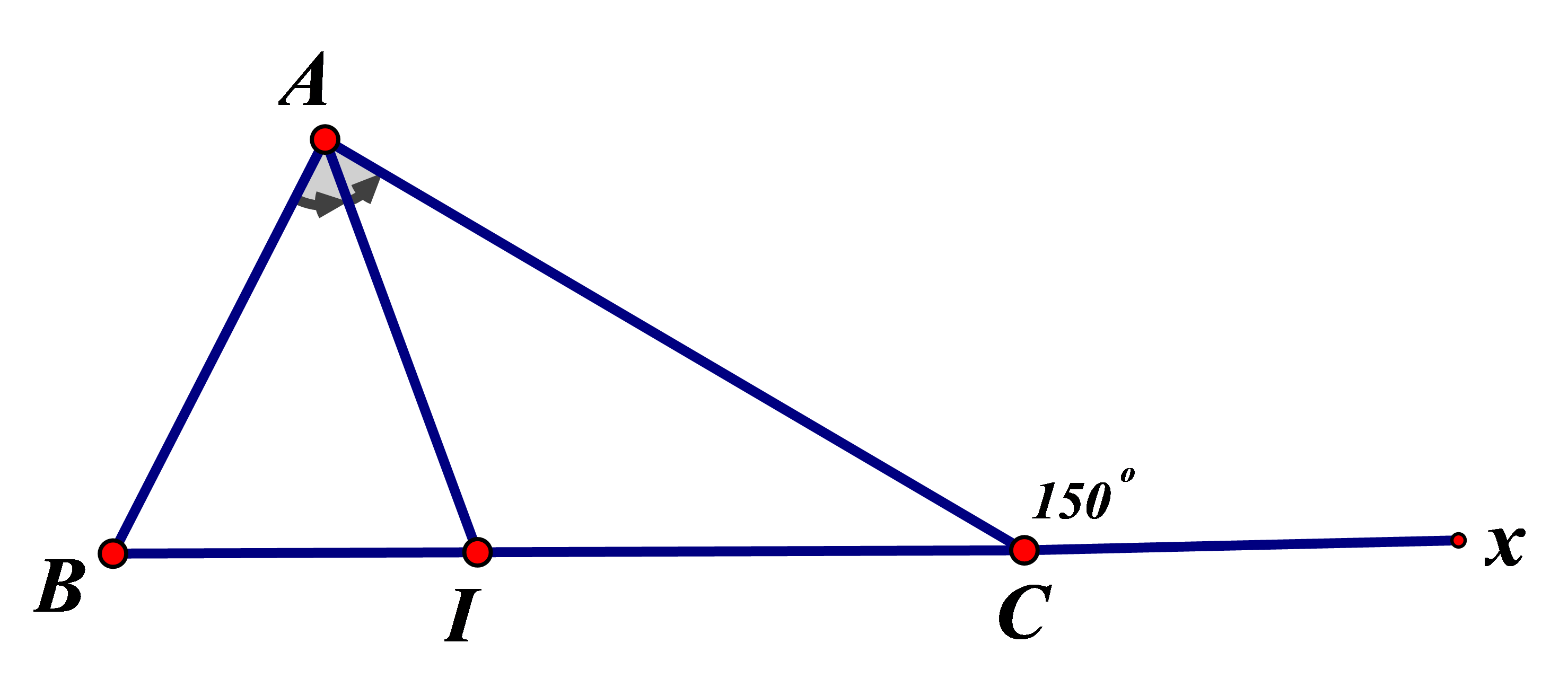
Dễ có: và
Nên
Bài 9: Vì nên .
Tam giác EFM có vuông tại E .
Tam giác KPN có vuông tại K .
Khi đó:
Bài 10:
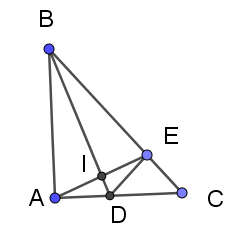
a)
Ta chứng minh được (vì cùng phụ với góc ACB).
b) Gọi I là giao điểm của AE và BD.
+ Chứng minh
Từ đó chứng minh được BD là đường trung trực của AE.
Xem thêm các dạng bài tập Toán lớp 7 có đáp án và lời giải chi tiết khác:
Tổng ba góc của một tam giác và cách giải các dạng bài tập
Tam giác cân, Tam giác đều và cách giải các dạng bài tập
Định lí Pi-ta-go và cách giải các dạng bài tập
Các trường hợp bằng nhau của hai tam giác vuông và cách giải
Xem thêm các chương trình khác:
