Các dạng bài tập về Số thực và cách giải – Toán lớp 7
Với cách giải các dạng toán về Số thực môn Toán lớp 7 Đại số gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về Số thực lớp 7. Mời các bạn đón xem:
Các dạng bài tập về Số thực và cách giải – Toán lớp 7
I. LÝ THUYẾT:
1. Số thực:
- Số hữu tỉ và số vô tỉ được gọi chung là số thực.
Tập hợp các số thực được ký hiệu là ℝ
- Nếu a là số thực thì a biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn. Khi đó, ta có thể so sánh hai số thực tương tự như so sánh hai số hữu tỉ viết dưới dạng thập phân.
- Với a, b là hai số thực dương, nếu a > b thì √a>√b
2. Trục số thực:
- Mỗi số thực được biểu diễn bởi một điểm trên trục số.
- Mỗi điểm trên trục số biểu diễn một số thực.
3. Các phép toán:
Trong tập hợp số thực ℝ , ta cũng định nghĩa các phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa và khai căn. Các phép toán trong tập hợp số thực cũng có các tính chất như các phép toán trong tập hợp các số hữu tỉ.
II. CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 10.1: Các câu hỏi và bài tập về định nghĩa các tập hợp số.
1. Phương pháp giải:
- Nắm vững các ký hiệu tập hợp số:
ℕ : tập hợp các số tự nhiên
ℤ: tập hợp các số nguyên
ℚ : tập hợp các số hữu tỉ
I: tập hợp các số vô tỉ
ℝ: tập hợp các số thực
- Nắm vững quan hệ giữa các tập hợp số nói trên: ; ℕ⊂ℤ⊂ℚ⊂ℝ;𝕀⊂ℝ
- Các kí hiệu∈; ∉ dùng để so sánh giữa phần tử với tập hợp.
- Các kí hiệu ⊂ dùng để so sánh giữa các tập hợp với nhau.
2. Ví dụ minh họa
Ví dụ 1: Điền kí hiệu (∈,∉,⊂) thích hợp vào ô trống:
 Giải:
Giải:


Dạng 10.2: So sánh các số thực.
1. Phương pháp giải:
Cần nắm vững:
- Với hai số thực x, y bất kỳ, ta luôn có x = y hoặc x < y hoặc x > y.
- Các số thực lớn hơn 0 gọi là số thực dương, các số thực nhỏ hơn 0 gọi là các số thực âm. Số 0 không là số thực dương cũng không là số thực âm.
- Việc so sánh các số thực dương làm tương tự như so sánh các số hữu tỉ.
- Với a, b là hai số thực dương, nếu a > b thì √a>√b
2. Ví dụ minh họa:
Ví dụ 2: Sắp xếp các số thực: −2,15; −3; 0; −√3; 137; 3312; √8 theo thứ tự từ bé đến lớn.
Giải:
Ta có:
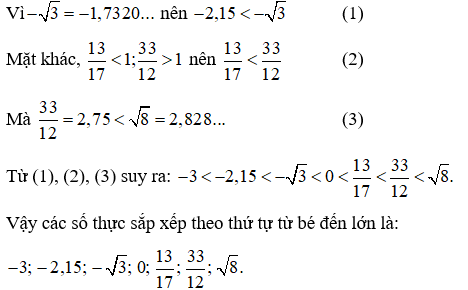
Dạng 10.3: Tìm một số chưa biết trong một đẳng thức.
1. Phương pháp giải:
- Sử dụng tính chất của các phép toán.
- Sử dụng quan hệ giữa các số hạng trong một tổng, một hiệu; quan hệ giữa các thừa số trong một tích, quan hệ giữa số bị chia, số chia và thương trong một phép chia.
- Sử dụng quy tắc dấu ngoặc, chuyển vế.
2. Ví dụ minh họa:
Ví dụ 3: Tìm x, biết:
a)0,75+0,4x=2960
b)23−0,6x=521
Giải:
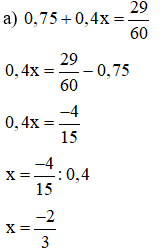
Vậy x=−23 là giá trị cần tìm.
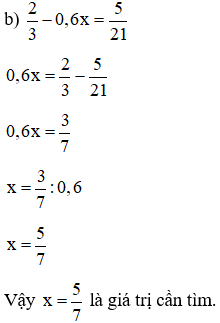
Dạng 10.4: Tìm giá trị của biểu thức.
1. Phương pháp giải:
- Thực hiện phối hợp các phép tính cộng, trừ, nhân, chia, lũy thừa, chú ý thực hiện đúng theo thứ tự đã quy định.
- Rút gọn các phân số khi có thể.
- Chú ý vận dụng tính chất các phép toán để tính toán được thuận tiện.
2. Ví dụ minh họa:
Ví dụ 4: Tính giá trị của các biểu thức:
(0,8.7+0,64).(114.7−0,8.114)+31,64
Giải:
(0,8.7+0,64).(114.7−0,8.114)+31,64
= (0,8.7 + 0,64).(1,25.7 - 0.8.1,25) + 31,64
= (5,6 + 0,64).(8,75 - 1) + 31,64
= 6,24.7.75 + 31.64
= 48,36 + 31,64
= 80.
III. BÀI TẬP VẬN DỤNG:
Bài 1: Điền dấu thích hợp vào ô trống.

Bài 2: So sánh các số thực sau:
a) 22,099 và 22,09(2209)
b) 116 và 1,8(3)
Bài 3: Sắp xếp các số thực sau theo thứ tự tăng dần:
0,466; 715 ; 0,4636363...; 0,463736; 0,4656365…
Bài 4: Sắp xếp các số thực:−2,15; −3; 0; −√3; 137; 3312; √8 theo thứ tự từ nhỏ đến lớn.
Bài 5: Tính giá trị của biểu thức:
A=(−1+325+14).(−4)
B=(0,645:0,3−151150):0,72−11,125
C=11,26−5,13:(4+114)
Bài 6: So sánh:
a) √6 và 3.
b) 5√6 và 6√5
Bài 7: Tính bằng cách hợp lí:
A = (+0,35) + [(+52,7) + (– 7,35) + (+4,3)]
B = (– 45,7) + [(+5,7) + (+5,75) + (– 0,75)]
C = [(+19,5) + (– 23)] + [(– 7) + (+10,5)]
Bài 8: Tìm x:
a) 3,5.x + (– 1,5).x + 3,2 = – 5,4
b) (– 7,2).x + 3,7.x + 2,7 = – 7,8
c) (213+312):(x+317)+712=16986
Bài 9:
a) Điền số thích hợp vào các đẳng thức:
√1=...√1+2+1=...√1+2+3+2+1=...
b) Chứng tỏ mọi n∈ℕ* ta có:
√1+2+...+(n−1)+n+(n−1)+...+2+1=n
Bài 10: Tìm x nguyên để các biểu thức sau có giá trị nguyên:
A=−3x+2x+2
B=3√x−22−√x
Hướng dẫn giải:
Bài 1:
a.∈ b.∉ c.∈ d.⊂
Bài 2: Đáp án:
a) > b) =
Bài 3:
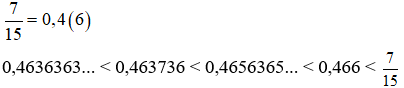
Bài 4:
Ta có −√3=−1,7320...⇒−2,15<−√3
1317<1; 3312>1⇒1317<3312
Mà 3312=2,75<√8=2,828...
⇒−3<−2,15<−√3<0<1317<3312<√8
Bài 5:
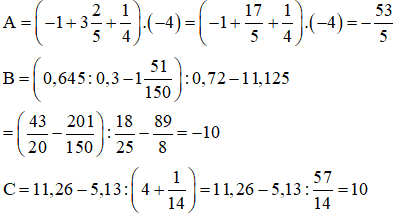
Bài 6:
a)√6<√9=3
b) (5√6)2=150<(6√5)2=180
⇒5√6<6√5
Bài 7:
A = 50 B = – 35 C = 0
Bài 8:
a) 3,5.x + (– 1,5).x + 3,2 = – 5,4
x(3,5 – 1,5) = – 5,4 – 3,2
2x = – 8,6
x = – 4,3
b) (– 7,2).x + 3,7.x + 2,7 = – 7,8
x(– 7,2 + 3,7) = – 7,8 – 2,7
x(– 3,5) = – 10,5
x = 3
c.
(213+312):(x+317)+712=16986
356:(x+227)=−24543x+227=−4342x=−256
Bài 9:

Bài 10:
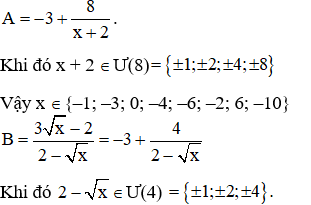
Xem thêm các dạng bài tập và công thức Toán lớp 7 hay, chi tiết khác:
Xem thêm các chương trình khác:
