Giá trị tuyệt đối của một số hữu tỉ và cách giải – Toán lớp 7
Với Giá trị tuyệt đối của một số hữu tỉ môn Toán lớp 7 Đại số gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về Giá trị tuyệt đối của một số hữu tỉ lớp 7. Mời các bạn đón xem:
Giá trị tuyệt đối của một số hữu tỉ và cách giải – Toán lớp 7
I. LÝ THUYẾT:
Giá trị tuyệt đối của một số hữu tỉ x, kí hiệu |x| là khoảng cách từ điểm x đến điểm 0 trên trục số.
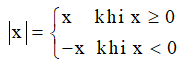
II. CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 3.1: Tính toán các số hữu tỉ có chứa dấu giá trị tuyệt đối.
1. Phương pháp giải:
- Định nghĩa giá trị tuyệt đối của một số hữu tỉ:
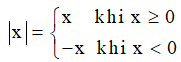
- Tính chất hay sử dụng của giá trị tuyệt đối:
∀x∈Z: |x|≥0;|x|=|-x|;|x|≥x
2. Ví dụ minh họa:
Ví dụ 1: Tính:
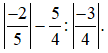
Giải:
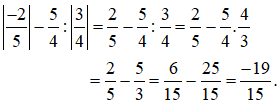
Dạng 3.2: Tìm một số chưa biết trong biểu thức có chứa dấu giá trị tuyệt đối.
1. Phương pháp giải:
- Áp dụng định nghĩa dấu giá trị tuyệt đối của một số hữu tỉ.
- Quy tắc chuyển vế.
- Tính chất hay sử dụng của giá trị tuyệt đối:
∀x∈Z: |x|≥0;|x|=|-x|;|x|≥x
2. Ví dụ minh họa:
Ví dụ 2: Tìm x, biết:
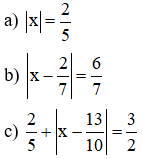
Giải:
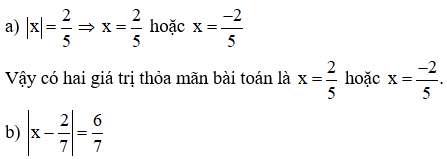
Cách 1: (Căn cứ vào định nghĩa của giá trị tuyệt đối)
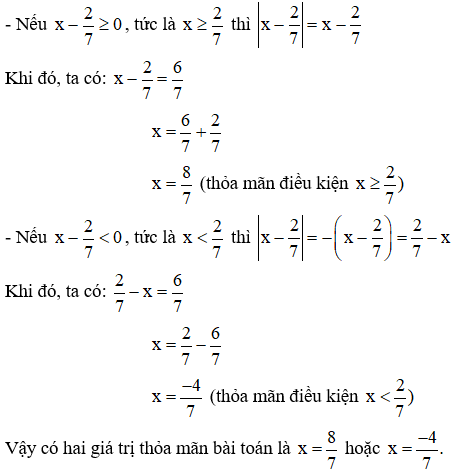
Cách 2: (Căn cứ vào tính chất |x| = |–x|).

Dạng 3.3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức có chứa giá trị tuyệt đối.
1. Phương pháp giải:
Cho biểu thức A thì |A|≥0 với m là hằng số, ta có:
+ Giá trị nhỏ nhất của |A| + m ≥ m.
+ Giá trị lớn nhất của –|A| + m ≤ m.
2. Ví dụ minh họa:
Ví dụ 3: Tìm giá trị nhỏ nhất của biểu thức:
A=|x-13|+4
Giải:
Vì |x-13|≥0∀x
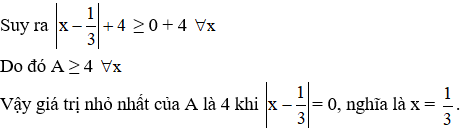
Ví dụ 4: Tìm giá trị lớn nhất của biểu thức:
B = 5,5 – |2x – 1,5|
Giải:
Vì |2x – 1,5| ≥ 0 ∀x
=> –|2x – 1,5| ≤ 0 ∀x
=> –|2x – 1,5| + 5,5 ≤ 5,5∀x
=> 5,5 – |2x – 1,5| ≤ 5,5 ∀x
Suy ra B ≤ 5,5 ∀x
Vậy giá trị lớn nhất của B là 5,5 khi |2x – 1,5|= 0, nghĩa là 2x – 1,5 = 0 hay x = 0,75.
III. BÀI TẬP VẬN DỤNG:
Bài 1: Trong các khẳng định sau đây, khẳng định nào đúng:
a) |–10,5| = 10,5;
b) –0,75| = –0,75;
c) |–15,25| = – (–15,25).
Bài 2: Tính:
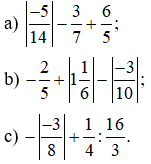
Bài 3: Tính giá trị của các biểu thức sau với: |a| = 1,5; b = –0,5.
a) A = a + b;
b) B = 2a – |3b|.
Bài 4: Tìm x, biết:
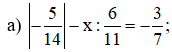
b) |x|=15
c) |x|=|-45|
Bài 5: Tìm x, biết:
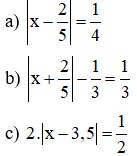
Bài 6: Tính giá trị biểu thức: A = 2x2 – 5x + 1 biết |x| = 13
Bài 7: Tìm giá trị nhỏ nhất của biểu thức:
a) A = |3,7 – x| + 2,5
b) B = |x + 1,5| – 4,5
Bài 8: Tính giá trị lớn nhất của biểu thức:
a) M=2-|x+23|
b)N=-|x-25|+2021
Bài 9: Tính giá trị của biểu thức:
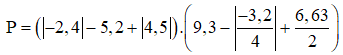
Bài 10: Tìm giá trị nhỏ nhất của biểu thức sau:
A = |x – 100| + |x – 400|
Hướng dẫn giải:
Bài 1:
a) Đúng (Vì –10,5 < 0 nên |–10,5| = –(–10,5) = 10,5).
b) Sai (vì |–0,75| = – (–0,75) = 0,75);
c) Đúng (vì |–15,25| = 15,25 = – (–15,25)).
Bài 2: (Bỏ dấu giá trị tuyệt đối rồi tính toán như bình thường).
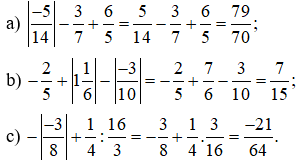
Bài 3:
a) Với a = 1,5; b = –0,5 A = a + b = 1
Với a = –1,5; b = –0,5 A = a + b = –2
b) Với a = 1,5; b = –0,5 B = 2a – |3b| = 1,5
Với a = –1,5; b = –0,5 B = 2a – |3b| = – 4,5
Bài 4:
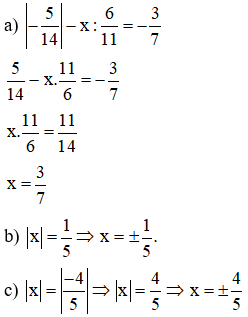
Bài 5: Tìm x, biết:
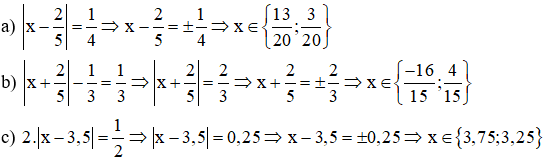
Bài 6: |x| = 13⇒x=±13
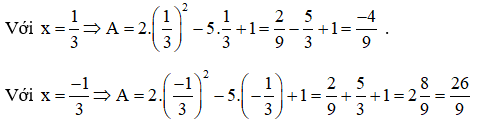
Bài 7: Giá trị nhỏ nhất của biểu thức:
a) A = |3,7 – x| + 2,5 ≥ 2,5. Dấu “=” xảy ra khi và chỉ khi x = 3,7
b) B = |x + 1,5| – 4,5 ≥ – 4,5. Dấu “=” xảy ra khi và chỉ khi x = –1,5
Bài 8: Giá trị lớn nhất của biểu thức:
a) M=2-|x+23| ≤ 2. Dấu “=” xảy ra khi và chỉ khi x =
b) N=-|x-25|+2021≤ 2021. Dấu “=” xảy ra khi và chỉ khi x =
Bài 9: Tính giá trị của biểu thức:
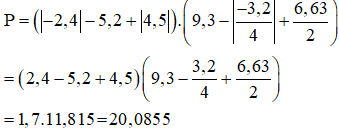
Bài 10:

Xem thêm các dạng bài tập và công thức Toán lớp 7 hay, chi tiết khác:
Xem thêm các chương trình khác:
