Đại lượng tỉ lệ thuận và cách giải các bài toán về đại lượng tỉ lệ thuận – Toán lớp 7

Đại lượng tỉ lệ thuận và cách giải các bài toán về đại lượng tỉ lệ thuận - Toán lớp 7

I. LÝ THUYẾT:

1. Định nghĩa.

 Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx (với k là hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.

Chú ý:

- Khi đại lượng y tỉ lệ thuận với đại lượng x thì x cũng tỉ lệ thuận với y và ta nói hai đại lượng đó tỉ lệ thuận với nhau.

- Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k (k ≠ 0) thì x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{k}$.

2. Tính chất:

Nếu hai đại lượng y và x tỉ lệ thuận với nhau, tức là với mỗi giá trị x₁, x₂, x₃,... khác 0 của x ta có một giá trị tương ứng y₁ =kx₁, y₂ = kx₂, y₃ =kx₃,… của y thì:

- Tỉ số hai giá trị tương ứng của chúng luôn luôn không đổi.

$\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=\mathrm{...}=k.$

- Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia.

$\frac{x_1}{x_2}=\frac{y_1}{y_2},\frac{x_1}{x_3}=\frac{y_1}{y_3},\mathrm{...}$

II. CÁC DẠNG BÀI TẬP CƠ BẢN:

Dạng 1.1: Tính hệ số tỉ lệ, biểu diễn x theo y, tính một giá trị khi biết giá trị kia.

1. Phương pháp giải: Áp dụng công thức y = kx để xác định tương quan tỉ lệ thuận giữa hai đại lượng và xác định hệ số tỉ lệ.

2. Ví dụ minh họa:

Ví dụ 1: Cho biết hai đại lượng x và y tỉ lệ thuận với nhau khi x = 9 thì y = 12.

a) Tìm hệ số tỉ lệ k của y đối với x;

b) Hãy biểu diễn y theo x;

c) Tính giá trị của y khi x = 6; x =15.

Giải:

Hai đại lượng x và y tỉ lệ thuận với nhau nên ta nói đại lượng y tỉ lệ thuận với đại lượng x và ta có công thức tổng quát là y = k.x.

a) Với x = 9, y = 12 ta có 12 = k.9

$\Rightarrow k=\frac{12}{9}=\frac{4}{3}.$

Vậy đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là $\frac{4}{3}$

b) Với $k=\frac{4}{3}$ , biểu diễn y theo x ta được $y=\frac{4}{3}x.$

c) Từ $y=\frac{4}{3}x$ ta có:

Với x = 6 thì $y=\frac{4}{3}.6=8.$

Với x =15 thì $y=\frac{4}{3}.15=20.$

Vậy khi x = 6 thì y = 8; x = 15 thì y = 20.

Dạng 1.2: Lập bảng giá trị tương ứng của hai đại lượng tỉ lệ thuận.

1. Phương pháp giải:

- Xác định hệ số tỉ lệ k.

- Dùng công thức y = kx, để tìm các giá trị tương ứng của x và y.

2. Ví dụ minh họa:

Ví dụ 2: Cho biết x và y là hai đại lượng tỉ lệ thuận. Hãy dựa vào bảng sau:

x	–4	–0,5	0	1,5	2,5	3	5
y	6

a) Tìm biểu thức liên hệ giữa hai đại lượng y và x.

b) Hoàn thành bảng.

Giải:

a) x và y là hai đại lượng tỉ lệ thuận nên y = k.x

Khi x = –4 thì y = 6 nên ta có $k=\frac{6}{-4}=\frac{-3}{2}$ 

Vậy y tỉ lệ thuận với x theo hệ số tỉ lệ $\frac{-3}{2}$, hay $y=\frac{-3}{2}x$

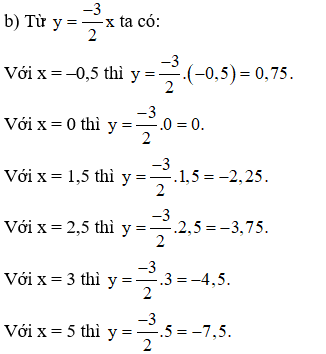
Vậy ta có bảng sau:

x	–4	–0,5	0	1,5	2,5	3	5
y	6	0,75	0	–2,25	–3,75	–4,5	–7,5

Dạng 1.3: Nhận biết hai đại lượng có tỉ lệ thuận không.

1. Phương pháp giải:

Dựa vào định nghĩa và tính chất của đại lượng tỉ lệ thuận.

Xem xét tất cả các thương của các giá trị tương ứng của hai đại lượng có bằng nhau không. Nếu bằng nhau, thì hai đại lượng cần xét là tỉ lệ thuận, nếu không bằng nhau thì hai đại lượng không phải là tỉ lệ thuận với nhau.

2. Ví dụ minh họa:

Ví dụ 3: Các giá trị tương ứng của t và s được cho trong bảng dưới đây:

t	– 4,5	3	1,1	–1,5	2,25	6,5
s	2,25	–1,5	$-\frac{11}{20}$	0,75	$-\frac{9}{8}$	$-\frac{13}{4}$
$\frac{s}{t}$

a) Điền giá trị thích hợp vào các ô trống trong bảng trên.

b) Hai đại lượng s và t có tỉ lệ thuận với nhau không? Nếu có hãy tìm hệ số tỉ  lệ của s với t?

Giải:

a) Ta có bảng sau:

t	– 4,5	3	1,1	–1,5	2,25	6,5
s	2,25	–1,5	$-\frac{11}{20}$	0,75	$-\frac{9}{8}$	$-\frac{13}{4}$
	– 0,5	– 0,5	– 0,5	–0,5	– 0,5	– 0,5

b) Vì  $\frac{s}{t}=-0,5$ (không đổi theo bảng ở câu a) nên s = – 0,5t.

Vậy s và t là hai đại lượng tỉ lệ thuận và đại lượng s tỉ lệ thuận với đại lượng t theo hệ số tỉ lệ là – 0,5.

Dạng 1.4: Các bài toán về đại lượng tỉ lệ thuận.

1. Phương pháp giải:

Bài toán 1: Toán về đại lượng tỉ lệ thuận.

- Xác định tương quan tỉ lệ thuận giữa hai đối tượng.

- Áp dụng tính chất về tỉ số các giá trị của hai đại lượng tỉ lệ thuận.

Bài toán 2: Chia một số thành những phần tỉ lệ thuận với các số cho trước.

Giả sử phải chia số S thành ba phần x, y, z tỉ lệ với các số a, b, c. Ta có: $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x+y+z}{a+b+c}=\frac{S}{a+b+c}.$  (áp dụng tính chất của dãy tỉ số bằng nhau để giải quyết).

Do đó,

$x=\frac{S}{a+b+c}.a;y=\frac{S}{a+b+c}.b;z=\frac{S}{a+b+c}.c$

2. Ví dụ minh họa:

Ví dụ 4: Khi xát 100 kg thóc thì được 60 kg gạo. Hỏi phải xát bao nhiêu kg thóc để được 1200 kg gạo?

Giải:

Vì khối lượng thóc y (kg) tỉ lệ thuận với khối lượng gạo x (kg) nên ta có y = k.x

Theo điều kiện đề bài, x = 60 thì y = 100 suy ra 100 = k.60 hay $k=\frac{5}{3}.$

Do đó $y=\frac{5}{3}x.$

Khi x = 1200 (kg) thì $y=\frac{5}{3}.1200=2000\left(kg\right).$

Vậy phải xát 2000 kg thóc để được 1200 kg gạo.

Ví dụ 5: Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3 : 4 : 6. Hỏi mỗi đơn vị được chia bao nhiêu tiền nếu tổng số tiền lãi là 650 triệu đồng và tiền lãi được chia tỉ lệ thuận với số tiền đóng góp?

Giải:

Gọi số tiền lãi ba đơn vị kinh doanh thu được lần lượt là x, y, z (triệu đồng).

Vì số tiền lãi tỉ lệ thuận với số vốn đã góp nên ta có:

x : y : z = 3 : 4 : 6

$\Rightarrow \frac{x}{3}=\frac{y}{4}=\frac{z}{6}$

Tổng số tiền lãi là 650 triệu đồng nên x + y + z = 650

Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{3}=\frac{y}{4}=\frac{z}{6}=\frac{x+y+z}{3+4+6}=\frac{650}{13}=50$

Do đó:

$\frac{x}{3}=50\Rightarrow x=3.50=150$

$\frac{y}{4}=50\Rightarrow y=4.50=200$

$\frac{z}{6}=50\Rightarrow z=6.50=300$

Vậy số tiền lãi được chia cho các đơn vị kinh doanh theo thứ tự là 150 triệu, 200 triệu và 300 triệu.

III. BÀI TẬP VẬN DỤNG:

Bài 1: Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là k = –2. Hỏi x tỉ lệ thuận với y theo hệ số nào?

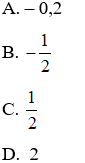
Bài 2: Biết rằng 14 dm³  sắt cân nặng 109,2 kg . Hỏi 14 m³  sắt cân nặng bao nhiêu kg?

Bài 3: Khối lượng m (g) của một thanh kim loại đồng chất có khối lượng riêng là 9,3 (g /cm³) tỉ lệ thuận với thể tích V (cm³) theo công thức m = 9,3 V. Khi V = 3 thì giá trị tương ứng của m là:

A. 18,6g

B. 27,9g

C. 37,2g

D. 46,5g

Bài 4: Một công nhân làm được 20 sản phẩm trong 1 giờ. Hỏi trong 90 phút người đó làm được bao nhiêu sản phẩm?

Bài 5: Hai đại lượng x và y có tỉ lệ thuận với nhau hay không, nếu:

a)

x	2,3	4,8	– 9	– 6	– 5
y	4,8	2,3	– 5	– 6	– 9

b)

x	– 5,1	– 6,2	– 7,3	– 8,4	– 9,5
y	2,04	2,48	2,92	3,36	3,8

Bài 6: Tổng số tiền điện phải trả của ba hộ sử dụng điện trong một tháng là 550 000 đồng. Biết rằng số điện năng tiêu thụ của ba hộ tỉ lệ với 5; 7; 8. Tính số tiền điện mỗi hộ phải trả.

Bài 7:

a) Trong 3 lít nước biển chứa 105 gam muối. Hỏi 150 lít nước biển chứa bao nhiêu kg muối?

b) Khi xát 100kg thóc thì được 62kg gạo. Hỏi phải xát bao nhiêu kg thóc để được 155kg gạo?

c) Biết rằng 21 lít dầu hỏa nặng 16,8kg. Hỏi 19kg dầu hỏa có chứa được hết vào chiếc can 23 lít không?

Bài 8: Số M được chia thành ba phần tỉ lệ với nhau như $0,5:1\frac{2}{3}:2\frac{1}{4}.$ Tìm số M, biết rằng tổng bình phương của ba số đó bằng 4660.

Bài 9: Cho biết x, y là hai đại lượng tỉ lệ thuận, x₁, x₂ là hai giá trị khác nhau của x; y₁, y₂ là hai giá trị tương ứng của y.

a) Tính x₂, y₂ biết x₂ + y₂ =10, x₁ = 3, y₁ = 2.

b) Tìm x₁, y₁ biết 2y₁ + 3x₁ = 20, x₂ = –6, y₂ =3.

Bài 10: Tổng số tiền lương của ba bác công nhân A, B, C là 1 350 000 đồng. Đợt 1 mỗi bác nhận được 200 000 đồng. Đợt 2 số tiền ba bác A, B và C nhận được tỉ lệ thuận với 2; 2,5 và 3 . Hỏi cả hai đợt mỗi bác nhận được bao nhiêu tiền lương?

Hướng dẫn giải:

Bài 1: Đáp án: B

Bài 2: Đáp số: 109 200 kg.

Bài 3: Đáp án: B

Bài 4: Đáp số: 30 sản phẩm.

Bài 5:

a) Không.

b) Có.

Bài 6: Gọi số tiền điện mỗi hộ phải trả lần lượt là: a, b, c (đồng)

Ta có:

$\frac{a}{5}=\frac{b}{7}=\frac{c}{8}=\frac{a+b+c}{20}=\frac{550000}{20}=27500$

 a =137 500; b = 192 500; c = 220 000.

Bài 7:

a) Khối lượng muối tỉ lệ thuận với số lít nước biển.

Gọi số kg muối từ 150 lít nước biển là x.

Ta có $\frac{3}{105}=\frac{150}{x}\Rightarrow x=5250\left(g\right)=5,25\left(kg\right)$

b) Khối lượng gạo tỉ lệ thuận với khối lượng thóc.

Gọi khối lượng thóc cần để thu được từ 155 kg gạo là x.

Ta có $\frac{100}{62}=\frac{x}{155}\Rightarrow x=250\left(kg\right)$

c) Không chứa hết. Cách làm tương tự các câu trên, 19 kg dầu hỏa ứng với 23,75 lít nên không chứa hết vào can 23 lít.

Bài 8: Đáp án: 12; 40; 54 hoặc –12; – 40; – 54.

Bài 9:

a) Ta có $\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{2}{3}$ .

Mặt khác, x₂ + y₂ = 10.

Từ đó suy ra x₂ = 6; y₂ =4.

b) Ta có $\frac{y_1}{x_1}=\frac{y_2}{x_2}=-\frac{1}{2}$ 

Mà 2y₁ + 3x₁ = 20.

Từ đó suy ra x₁ = 10; y₁ = – 5.

Bài 10: Tổng số tiền đợt hai cả ba bác nhận được là:

1 350 000 – 200 000 . 3 = 750 000 đồng

Đợt 2 mỗi bác nhận được số tiền là:

A: 200 000 đồng

B:  250 000 đồng

C: 300 000 đồng

Vậy sau 2 tháng mỗi bác nhận được số tiền là:

A: 400 000 đồng

B: 450 000 đồng

C: 500 000 đồng.