Các dạng toán về Tập hợp Q các số hữu tỉ và cách giải

Các dạng toán về Tập hợp Q các số hữu tỉ và cách giải

I. Lý thuyết về số hữu tỉ

1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số

- Số hữu tỉ là các số có thể biểu diễn được dưới dạng phân số $\frac{a}{b}\left(a,b\in \mathbb{Z},b\ne 0\right).$

- Tập hợp các số hữu tỉ được kí hiệu là $\mathbb{Q}$ (x là số hữu tỉ thì ghi là $x\in \mathbb{Q}$)

- Ta có thể biểu diễn mọi số hữu tỉ trên trục số. Trên trục số, điểm biểu diễn số hữu tỉ được gọi là điểm x.

+ Các số nguyên ta đã biết biểu diễn trên trục số.

+ Tương tự cách biểu diễn số nguyên ta biểu diễn số hữu tỉ $\frac{a}{b}\left(a,b\in {\mathbb{Z}}^{+},b\ne 0\right)$ như sau:

Chia đoạn có độ dài 1 đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới thì điểm biểu diễn số hữu tỉ $\frac{a}{b}$ cách gốc 0 là a đơn vị mới.

+ Với số hữu tỉ $\frac{a}{b}$ có tử số và mẫu số trái dấu ta biểu diễn tương tự nhưng chia đoạn 1 đơn vị bên trái gốc 0.

Ví dụ: Để biểu diễn số hữu tỉ $\frac{3}{5}$ ta chia đoạn 1 đơn vị thành 5 phần, điểm biểu diễn số $\frac{3}{5}$ như hình vẽ:

- Với hai số hữu tỉ bất kỳ x, y ta luôn có hoặc x = y hoặc x < y hoặc x > y. Ta có thể so sánh hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

+ Nếu x < y thì trên trục số, điểm x ở bên trái điểm y;

+ Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương;

+ Số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm;

+ Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

2. Thứ tự trong tập hợp các số hữu tỉ

• Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

• Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số, nếu a < b thì điểm a nằm trước điểm b.

Ví dụ:

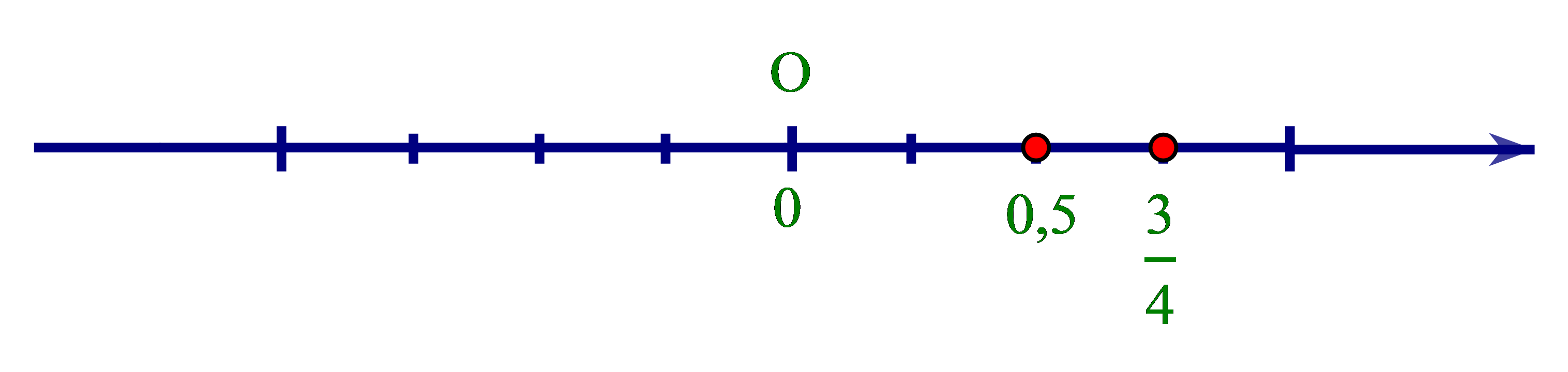
+ So sánh 0,5 và $\frac{3}{4}$ ta làm như sau:

Ta có 0,5 = $\frac{5}{10}=\frac{1}{2}=\frac{2}{4}$

Vì 2 < 3 nên $\frac{2}{4}$ < $\frac{3}{4}$hay 0,5 < $\frac{3}{4}$ .

+ 0,5 < $\frac{3}{4}$ nên 0,5 nằm trước $\frac{3}{4}$ trên trục số.

+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ $\frac{5}{6}$ và $\frac{6}{5}$ như sau:

Vì $\frac{5}{6}<\frac{6}{6}=1$ và $1=\frac{5}{5}<\frac{6}{5}$ nên $\frac{5}{6}$ < 1 < $\frac{6}{5}$ .

Vậy $\frac{5}{6}<\frac{6}{5}$ .

Chú ý:

• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.

II. Các dạng bài tập cơ bản

Dạng 1.1: Sử dụng các ký hiệu $\in$, $\notin$, $\subset$, $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}.$

1. Phương pháp giải:

Nắm vững ý nghĩa của từng ký hiệu:

- Kí hiệu $\in$ đọc là “phần tử của” hoặc “thuộc”.

- Kí hiệu $\notin$ đọc là “không phải là phần tử của” hoặc “không thuộc”.

- Kí hiệu $\subset$ đọc là “là tập hợp con của”.

- Kí hiệu $\mathbb{N}$ chỉ tập hợp các số tự nhiên.

- Kí hiệu $\mathbb{Z}$ chỉ tập hợp các số nguyên.

- Kí hiệu $\mathbb{Q}$ chỉ tập hợp các số hữu tỉ.

- Các kí hiệu $\in$; $\notin$ dùng để so sánh giữa phần tử với tập hợp.

- Các kí hiệu $\subset$ dùng để so sánh giữa các tập hợp với nhau.

2. Ví dụ minh họa:

Ví dụ 1: Điền kí hiệu $(\in ,\notin ,\subset )$ thích hợp vào ô trống:

5 $\square$ $\mathbb{N}$ -4 $\square$ $\mathbb{Z}$

-2 $\square$ $\mathbb{Q}$ $\frac{-3}{5} \square \mathbb{Z}$

$\frac{-3}{5} \square \mathbb{Q}$ $\mathbb{N} \square \mathbb{Z} \square \mathbb{Q}$

Giải:

Các kí hiệu $\in ; \notin$ dùng để so sánh giữa phần tử với tập hợp.

Các kí hiệu $\subset$ dùng để so sánh giữa các tập hợp với nhau.

Vì 5 là số tự nhiên nên 5$\in \mathbb{N}$

Vì – 4 là số nguyên nên – 4$\in \mathbb{Z}$

Vì $-2=\frac{-2}{1}$ nên – 2 có thể biểu diễn được dưới dạng số hữu tỉ.

Do đó – 2$\in \mathbb{Q}.$

Vì $-3\cancel{⋮}5$ nên $\frac{-3}{5}$ không phải là số nguyên. Do đó $\frac{-3}{5}\notin \mathbb{Z}.$

Vì $\frac{-3}{5}$ biểu diễn dưới dạng $\frac{a}{b}\left(a,b\in \mathbb{Z},b\ne 0\right)$ nên $\frac{-3}{5}$ là số hữu tỉ. Do đó

Vì mọi số nguyên đều biểu diễn được dưới dạng số hữu tỉ nên $\mathbb{Z}\subset \mathbb{Q},$ mà nên

Từ đó, ta điền ký hiệu thích hợp vào ô trống như sau:

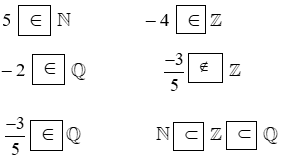
Dạng 1.2: Biểu diễn số hữu tỉ

1. Phương pháp giải:

- Số hữu tỉ thường được biểu diễn dưới dạng phân số tối giản.

- Khi biểu diễn số hữu tỉ trên trục số, ta thường viết số đó dưới dạng phân số tối giản có mẫu dương. Khi đó mẫu của phân số cho biết đoạn thẳng đơn vị cần được chia thành bao nhiêu phần bằng nhau.

+ Trường hợp 1: a > 0, khi đó $\frac{a}{b}$ là số hữu tỉ dương, ta chia khoảng có độ dài 1 đơn vị làm b phần bằng nhau, ta được đơn vị mới bằng $\frac{1}{b}$ đơn vị cũ, tiếp theo lấy về phía chiều dương trục Ox a phần, ta được vị trí của số $\frac{a}{b}$.

+ Trường hợp 2: a < 0, khi đó $\frac{a}{b}$ là số hữu tỉ âm, ta chia khoảng có độ dài 1 đơn vị làm b phần bằng nhau, ta được đơn vị mới bằng $\frac{1}{b}$ đơn vị cũ, tiếp theo lấy về phía chiều âm trục Ox a phần, ta được vị trí của số $\frac{a}{b}$.

2. Ví dụ minh họa:

Ví dụ 2:

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{2}{-5}:$

$\frac{-6}{15};\frac{-3}{15};\frac{12}{-30};\frac{6}{20};\frac{-10}{35}?$

b) Biểu diễn số hữu tỉ $\frac{2}{-5}$ trên trục số.

Giải:

a) Ta có $\frac{2}{-5}=\frac{-2}{5}$. Rút gọn các phân số đã cho ta được:

$\frac{-6}{15}=\frac{-2}{5};\frac{-3}{15}=\frac{-1}{5};\frac{12}{-30}=\frac{-2}{5};$ $\hspace{0.17em}\frac{6}{20}=\frac{3}{10};\frac{-10}{35}=\frac{-2}{7}.$

Vậy các phân số biểu diễn số hữu tỉ $\frac{2}{-5}$ là $\frac{-6}{15};\frac{12}{-30}.$

b) Vì $-1<\frac{2}{-5}<0$ nên $\frac{2}{-5}$ nằm giữa -1 và 0 trên trục số, ta chia đoạn này thành 5 phần. Phân số $\frac{2}{-5}$ được biểu diễn trên trục số như sau:

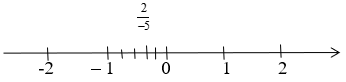
Dạng 1.3: So sánh các số hữu tỉ

1. Phương pháp giải:

Ta có thể so sánh hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó bằng một trong các cách sau:

- Đưa về các phân số có cùng mẫu số dương rồi so sánh tử số.

- So sánh với số 0, so sánh với số 1, với –1,…

- Dựa vào phần bù của 1: So sánh các phần bù rồi suy ra kết quả.

- So sánh với phân số trung gian.

- Có thể sử dụng tính chất sau: Nếu a, b, c $\in \mathbb{Z}$ và a < b thì a + c < b + c

2. Ví dụ minh họa:

Ví dụ 3: So sánh các số hữu tỉ:

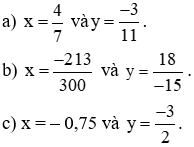
Giải:

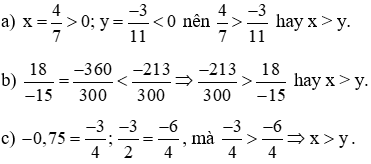
III. BÀI TẬP VẬN DỤNG

1. Bài tập có đáp án

Bài 1. So sánh:

a) – 1,25 và – 1,125;

b) 0,8 và $\frac{8}{15}$ ;

c) $-\frac{2}{19}$ và $-\frac{10}{19}$ ;

d) $2\frac{2}{3}$ và $\frac{17}{6}$ ;

e) $\frac{1}{2022}$và $\frac{1}{2023}$ ;

f) – 5,6 và $\frac{1}{2}$ ;

g) $\frac{7}{9}$ và 1,5.

Hướng dẫn giải

a) Có 1,25 > 1,125 nên – 1,25 < – 1,125

b) Có $0,8=\frac{8}{10}=\frac{4}{5}=\frac{12}{15}$ , vì $\frac{12}{15}>\frac{8}{15}$ . Nên $0,8 >\frac{8}{15}$

c) Có $\frac{2}{19}<\frac{10}{19}$ nên $-\frac{2}{19}<-\frac{10}{19}$

d) Có $2\frac{2}{3}=\frac{8}{3}=\frac{16}{6}$ , vì $\frac{16}{6}<\frac{17}{6}$. Nên $2\frac{2}{3}<\frac{17}{6}$

e) $\frac{1}{2022}>\frac{1}{2023}$

f) Có – 5,6 < 0 và $\frac{1}{2}$> 0. Nên – 5,6 < $\frac{1}{2}$

g) Có $\frac{7}{9}$< 1 và 1,5 > 1. Nên $\frac{7}{9}$< 1,5.

Bài 2. Điền kí hiệu (∈, ∉) thích hợp vào chỗ chấm:

a) 0,15 … $\mathrm{\mathbb{Q}}$ ;

b) $-\frac{5}{0}$ … $\mathrm{\mathbb{Q}}$ ;

c) 1,0 … $\mathrm{\mathbb{Q}}$ ;

d) $\frac{1,2}{8}$ … $\mathrm{\mathbb{Q}}$ .

Hướng dẫn giải

a) Vì 0,15 = $\frac{15}{100}=\frac{3}{20}$ (trong đó 3; 20 ∈ ℤ và 20 ≠ 0) nên 0,15 $\in \mathrm{\mathbb{Q}}$

b) Ta có: $-\frac{5}{0}$ (trong đó 5; 0 ∈ ℤ và 0 = 0) nên $-\frac{5}{0}\notin \mathrm{\mathbb{Q}}$

c) Vì 1, 0 = $\frac{1}{1}$ (trong đó 1; 1 ∈ ℤ và 1 ≠ 0) nên 1,0 $\in \mathrm{\mathbb{Q}}$

d) Vì $\frac{1,2}{8}=1,2:8=\frac{12}{10}:8=\frac{12}{10}.\frac{1}{8}=\frac{3}{10}$ (trong đó 3; 10 ∈ ℤ và 10 ≠ 0) nên $\frac{1,2}{8}\in \mathrm{\mathbb{Q}}$.

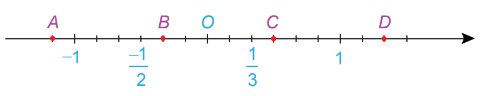
Bài 3. Cho trục số sau:

a) Các điểm A, B, C, D biểu diễn những số hữu tỉ nào?

b) Tìm số đối của các số hữu tỉ trên và biểu diễn chúng trên trục số.

Hướng dẫn giải

a) Ta thấy đoạn thẳng đơn vị cũ (ví dụ đoạn từ 0 đến 1) được chia thành 5 phần bằng nhau nên đoạn đơn vị mới bằng $\frac{1}{5}$ đơn vị cũ. Do đó:

Điểm A nằm trước gốc O và cách gốc O một khoảng bằng 7 đơn vị nên nó biểu diễn số hữu tỉ $-\frac{7}{5}$ .

Tương tự, ta có được:

Điểm B biểu diễn số hữu tỉ $-\frac{2}{5}$ .

Điểm C biểu diễn số hữu tỉ $\frac{4}{5}$ .

Điểm D biểu diễn số hữu tỉ $\frac{9}{5}$ .

b) Số đối của $-\frac{7}{5}$là $-\left(-\frac{7}{5}\right)=\frac{7}{5}$

Số đối của $-\frac{2}{5}$là $-\left(-\frac{2}{5}\right)=\frac{2}{5}$

Số đối của $\frac{4}{5}$là $-\frac{4}{5}$

Số đối của $\frac{9}{5}$là $-\frac{9}{5}$

Biểu diễn trên trục số:

A2. Bài tập trắc nghiệm

Bài 4. Trong các số hữu tỉ: $-1\frac{1}{2}$; -5; 0,75; $\frac{4}{5}$ . Số đối của số hữu tỉ lớn nhất là

A. $\frac{4}{5}$ ;

B. 5;

C. – 0,75;

D. $-\frac{4}{5}$.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: $-1\frac{1}{2}=\frac{-3}{2}$; $-5=\frac{-10}{2}$mà $\frac{-10}{2}<\frac{-3}{2}<0$ nên $-5<-1\frac{1}{2}<0$

$0,75=\frac{3}{4}=\frac{15}{20}$; $\frac{4}{5}=\frac{16}{20}$ mà $\frac{16}{20}>\frac{15}{20}>0$ nên $\frac{4}{5}>0,75>0$

Do đó: $-5<-1\frac{1}{2}<0,75<\frac{4}{5}$

Suy ra số lớn nhất là $\frac{4}{5}$ .

Vậy số đối của $\frac{4}{5}$là $-\frac{4}{5}$ .

Bài 5. Điểm biểu diễn số đối của của số hữu tỉ $\frac{-1}{2}$ là

A. điểm A;

B. điểm B;

C. điểm C;

D. điểm D.

Hướng dẫn giải

Đáp án đúng là: C

Điểm biểu diễn số hữu tỉ đối của $\frac{-1}{2}$ nằm khác phía với $\frac{-1}{2}$ so với điểm O. Như vậy điểm này nằm sau O.

Khoảng cách tử O đến $\frac{-1}{2}$ là 3 đoạn nên khoảng cách từ O đến điểm đó cũng là 3 đoạn.

Vậy điểm biểu diễn số hữu tỉ đối của $\frac{-1}{2}$ là điểm C.

Bài 6. Tập hợp số hữu tỉ được kí hiệu là

A. ℕ;

B. ℤ;

C. ℚ;

D. ℝ.

Hướng dẫn giải

Đáp án đúng là: C

Tập hợp số hữu tỉ được kí hiệu là ℚ.

2. Bài tập tự luyện

Bài 1: Điền kí hiệu $(\in ,\notin ,\subset )$ thích hợp vào ô trống:

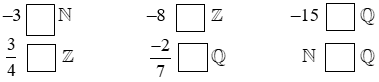
Bài 2:

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{5}{-4}:$

$\frac{10}{-8};\frac{-20}{16};\frac{40}{-28};\frac{-25}{20};\frac{-45}{35}?$

b) Biểu diễn số hữu tỉ $\frac{5}{-4}$ trên trục số.

Bài 3: So sánh các số hữu tỉ:

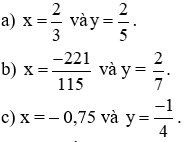
Bài 4: Điền kí hiệu thích hợp vào ô trống:

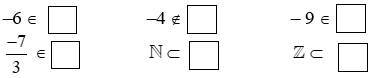
Bài 5: Viết ba số hữu tỉ xen giữa các số hữu tỉ sau:

a) $\frac{1}{3}$ và $\frac{1}{4}$

b) $\frac{-1}{10}$ và $\frac{-1}{100}$.

Bài 6: Trên giá sách có 40 quyển sách Toán, 20 quyển sách Văn. Lập tỉ số của các loại sách với số sách đang có trên giá.

Bài 7: Cho a$\in \mathbb{Z},$ b$\in \mathbb{Z},$ b > 0, $n\in \mathbb{N}*.$ Hãy so sánh hai số hữu tỉ $\frac{a}{b}$ và $\frac{a+n}{b+n}.$

Bài 8: So sánh các phân số sau bằng cách nhanh nhất (không quy đồng):

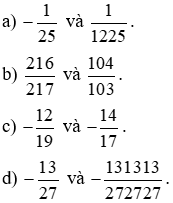
Bài 9: Cho số hữu tỉ $x=\frac{a-3}{2}.$ Với giá trị nào của a thì:

a) x là số dương;

b) x là số âm;

c) x không là số dương và cũng không là số âm.

Bài 10: Cho số hữu tỉ $y=\frac{2a-1}{-3}.$ Với giá trị nào của a thì:

a) y là số dương;

b) y là số âm;

c) y không là số dương và cũng không là số âm.

Hướng dẫn giải:

Bài 1: Đáp số:

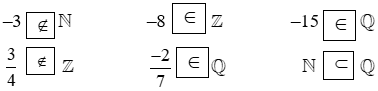
Bài 2:

a) Ta có $\frac{5}{-4}=\frac{-5}{4}$. Rút gọn các phân số đã cho, ta được: $\frac{10}{-8}=\frac{-5}{4};$$\hspace{0.17em}\frac{-20}{16}=\frac{-5}{4};$$\frac{40}{-28}=\frac{-10}{7};$$\hspace{0.17em}\frac{-25}{20}=\frac{-5}{4};$$\frac{-45}{35}=\frac{-9}{7}$

Vậy các phân số biểu diễn số hữu tỉ $\frac{5}{-4}$ là $\frac{10}{-8};\frac{-20}{16};\frac{-25}{20}.$

b) $-2<\frac{5}{-4}<-1$ nên $\frac{5}{-4}$ nằm giữa –2 và –1 trên trục số và chia khoảng này thành 4 phần để lấy biểu diễn số hữu tỉ $\frac{5}{-4}.$

Bài 3: So sánh các số hữu tỉ:

a) Hai phân số $\frac{2}{3} và \frac{2}{5}$ có cùng tử số, mẫu số của phân số nào lớn hơn thì bé hơn.

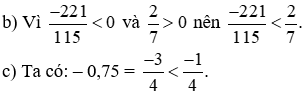
Bài 4:

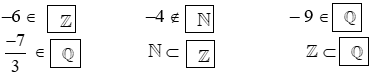
Bài 5: Viết ba số hữu tỉ xen giữa các số hữu tỉ sau:

a) Quy đồng hai phân số trên, mẫu số chung của hai phân số $\frac{1}{3} và \frac{1}{4}$ là B(48). Ta tìm ba phân số xen giữa $\frac{16}{48} và \frac{12}{48}$

b) $\frac{-1}{10}=-0,1; \frac{-1}{100}=-0,01$

Bài 6: Tổng số sách là 40 + 20 = 60 quyển.

Tỉ lệ sách Toán và Văn so với tổng số sách trên giá lần lượt là: $\frac{40}{60}=\frac{2}{3};\frac{20}{60}=\frac{1}{3}.$

Bài 7:

Ta có: a(b + n) = ab + an

b(a + n) = ab + bn

Vì b > 0, $n\in \mathbb{N}*$ nên b + n > 0

+) Nếu a > b thì ab + an > ab + bn

$\Rightarrow$a(b + n) > b(a + n)

+) Nếu a < b thì ab + an < ab + bn

$\Rightarrow$a(b + n) < b(a + n)

$\Rightarrow \frac{a}{b}<\frac{a+n}{b+n}.$

+) Nếu a = b thì $\frac{a}{b}=\frac{a+n}{b+n}.$

Bài 8:

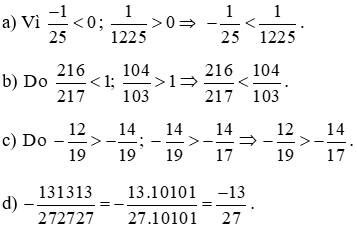
Bài 9: Cho số hữu tỉ $x=\frac{a-3}{2}.$

a) x là số dương khi tử số và mẫu số cùng dấu.

Mà mẫu số là 2 > 0 nên tử số là a – 3 > 0. Vậy a > 3.

b) x là số âm khi tử số và mẫu số khác dấu.

Mà mẫu số là 2 > 0 nên tử là số a – 3 < 0. Vậy a < 3.

c) x không là số dương và cũng không là số âm, nghĩa là x = 0.

Mà mẫu số là 2 ≠ 0 nên tử số a – 3 = 0 hay a = 3.

Bài 10: Cho số hữu tỉ $y=\frac{2a-1}{-3}.$ Với giá trị nào của a thì:

a) y là số dương khi tử số và mẫu số cùng dấu, mà mẫu số là –3 < 0 nên tử số bé hơn 0. Vậy $a<\frac{-1}{2}.$

b) y là số âm khi tử số và mẫu số khác dấu, mà mẫu số là –3 < 0 nên tử số lớn hơn 0. Vậy $a>\frac{-1}{2}.$

c) y không là số dương và cũng không là số âm, nghĩa là x = 0, có mẫu số là -3 ≠ 0 nên tử số bằng 0. Vậy $a=\frac{-1}{2}.$

Xem thêm các dạng bài tập và công thức Toán lớp 7 hay, chi tiết khác: