Các trường hợp bằng nhau của hai tam giác thường đầy đủ, chi tiết hay nhất - Toán lớp 7
Với Các trường hợp bằng nhau của hai tam giác thường đầy đủ, chi tiết Toán lớp 7 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các Các trường hợp bằng nhau của hai tam giác thường từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Các trường hợp bằng nhau của hai tam giác thường đầy đủ, chi tiết - Toán lớp 7
I. Lý thuyết
Định nghĩa hai tam giác bằng nhau: Hai tam giác bằng nhau là hai tam giác có csc cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
Cho tam giác ABC và tam giác A’B’C’.
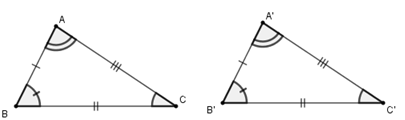
khi
1. Trường hợp bằng nhau thứ nhất (c – c – c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
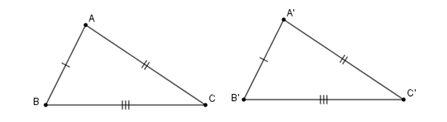
Xét tam giác ABC và tam giác A’B’C’
(c – c – c)
2. Trường hợp bằng nhau thứ hai (c – g – c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
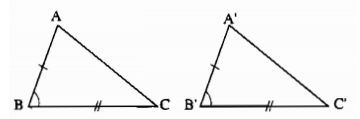
Xét tam giác ABC và tam giác A’B’C’ có:
(c – g – c)
3. Trường hợp bằng nhau thứ ba (g – c – g)
Nếu một cạnh và hai góc kề cạnh của tam giác này bằng một cạnh và hai góc kề cạnh của tam giác kia thì hai tam giác đó bằng nhau.
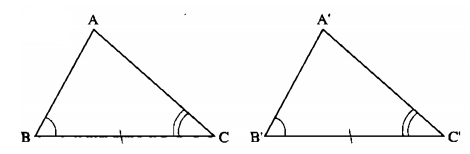
Xét tam giác ABC và tam giác A’B’C’ ta có:
(g – c – g)
II. Các ví dụ:
Ví dụ 1: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Chứng minh :
a) .
b) AM là tia phân giác của .
Lời giải:
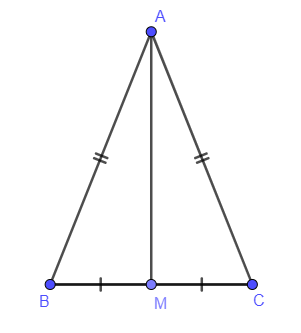
a) Xét tam giác ABM và tam giác ACM có:
AB = AC (giả thuyết)
BM = MC (do M là trung điểm của BC)
AM chung
Do đó (c – c – c)
(hai góc tương ứng).
b) Vì (hai góc tương ứng)
AM là phân giác của .
Ví dụ 2: Cho tam giác ABC có AB < AC. Phân giác của góc A cắt cạnh BC tại điểm D. Trên cạnh AC lấy E sao cho AE = AB. Chứng minh:
a) .
b) DA là tia phân giác của góc .
c) Chứng minh .
Lời giải:
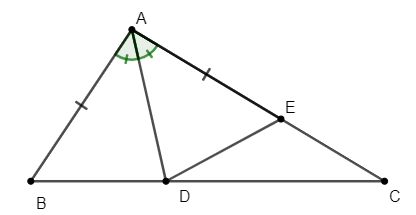
a) Vì AD là tia phân giác (tính chất)
Xét tam giác ABD và tam giác AED có:
AB = AE (giả thuyết)
(chứng minh trên)
AD chung
Do đó (c – g – c)
b) Vì (hai góc tương ứng)
DA là phân giác .
c) Vì nên (hai góc tương ứng) hay (1)
Xét tam giác DCE có là góc ngoài tại đỉnh E của tam giác
(tính chất góc ngoài của tam giác) (2)
Từ (1) và (2)
(điều phải chứng minh).
Ví dụ 3: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm M sao cho AM = AB. Qua M kẻ đường thẳng d song song với BC, đường thẳng d cắt CA tại N. Chứng minh:
a) ;
b) A là trung điểm của NC.
Lời giải:
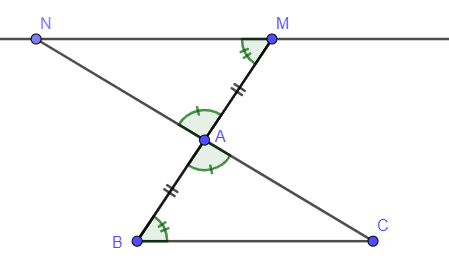
a) Vì đường thẳng d đi qua M song song với BC cắt AC tại N nên MN // BC.
(hai góc so le trong)
Xét tam giác AMN và tam giác ABC có:
(chứng minh trên)
AM = AB (giả thuyết)
(hai góc đối đỉnh)
Do đó: (g – c – g).
b) Vì (hai cạnh tương ứng)
Mà ba điểm A, N, C thẳng hàng
Nên A là trung điểm của NC.
Xem thêm tổng hợp công thức môn Toán lớp 7 đầy đủ và chi tiết khác:
Xem thêm các chương trình khác:
