Định lý Py-ta-go và định lý Py-ta-go đảo đầy đủ, chi tiết hay nhất - Toán lớp 7
Với Định lý Py-ta-go và định lý Py-ta-go đảo đầy đủ, chi tiết Toán lớp 7 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các công thức Định lý Py-ta-go và định lý Py-ta-go đảo từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Định lý Py-ta-go và định lý Py-ta-go đảo đầy đủ, chi tiết - Toán lớp 7
I. Lý thuyết
1. Định lý Py – ta – go
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương hai cạnh góc vuông.
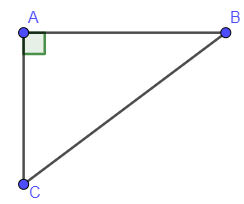
Tam giác ABC vuông tại A ta có:
2. Định lý Py – ta – go đảo
Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.
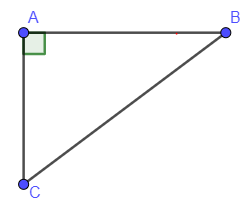
Xét tam giác ABC có: thì tam giác ABC vuông tại A.
II. Các ví dụ
Ví dụ 1: Tính độ dài AC, EF trong hình vẽ:
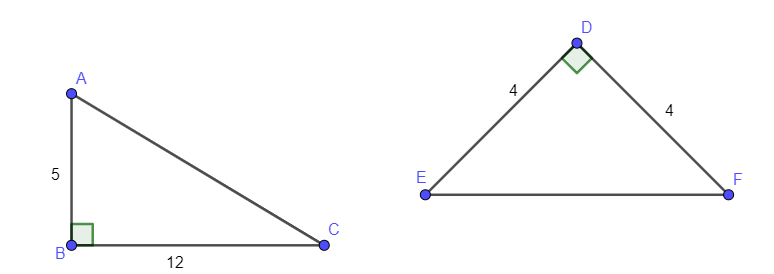
Lời giải:
+ Xét tam giác ABC vuông tại B ta có:
(định lý Py – ta – go)
(đơn vị độ dài)
+ Xét tam giác DEF vuông tại D ta có:
(định lý Py – ta – go)
(đơn vị độ dài)
Vậy AC = 13;
Ví dụ 2: Cho tam giác ABC vuông tại A có AB = 9cm, AC = 12cm. Tính BC.
Lời giải:
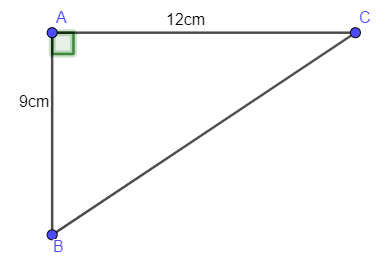
Áp dụng định lý Py – ta – go cho tam gác ABC vuông tại A ta có:
Ví dụ 3: Cho tam giác ABC có: AB = 6 cm; AC = 8 cm; BC = 10 cm. Chứng minh .
Lời giải:
Ta có:
vuông tại A (định lý Py – ta – go đảo)
(điều phải chứng minh)
Ví dụ 4: Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Gọi M là trung điểm của BC. Tính AM.
Lời giải:
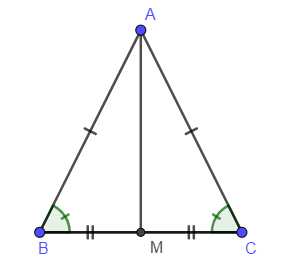
Vì ABC là tam giác cân (tính chất)
Vì M là trung điểm của BC nên MB = MC
Xét tam giác ABM và tam giác ACM có:
AB = AC (chứng minh trên)
(chứng minh trên)
MB = MC (chứng minh trên)
Do đó (c – g – c)
(hai góc tương ứng) (1)
Lại có: (hai góc kề bù) (2)
Từ (1) và (2)
Xét tam giác ABM vuông tại M có:
(định lý Py – ta – go)
Mà AB = 10cm; nên
Vậy AM = 8cm.
Xem thêm tổng hợp công thức môn Toán lớp 7 đầy đủ và chi tiết khác:
Xem thêm các chương trình khác: