Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 72 Tập 2 Cánh diều

    Với giải bài tập Toán lớp 7 trang 72 Tập 2 trong Bài 1: Tổng các góc của một tam giác sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 72 Tập 2.

    1 338 16/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 72 Tập 2

    Hoạt động 2 trang 72 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Tổng hai góc B và C bằng bao nhiêu độ?

    Lời giải

    GT

    Tam giác ABC vuông tại A.

    KL

    Tính B^+C^.  

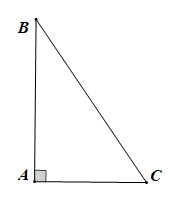
    Giải Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1) 

    Tam giác ABC vuông tại A (giả thiết) nên A^=90°. 

    Mà A^+B^+C^=180° (tổng ba góc của một tam giác).

    Suy ra B^+C^=180°−A^=180°−90°=90°. 

    Vậy .B^+C^=90°..

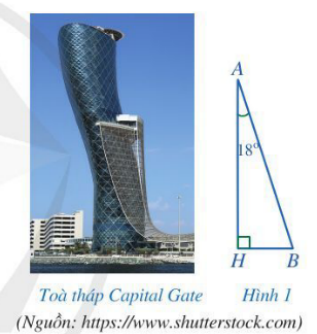
    Luyện tập 2 trang 72 Toán 7 Tập 2: Trong bài toán nêu ở phần mở đầu, hãy tính độ nghiêng của toà tháp Captial Gate so với phương nằm ngang.

    Giải Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1) 

    Lời giải

    Toà tháp Captial Gate được mô tả như Hình 1.

    Bài toán trở thành tính số đo góc B.

    GT

    Tam giác ABH vuông tại H

    A^=18° 

    KL

    Tính B^.  

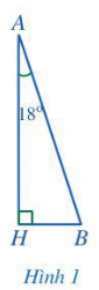
    Giải Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1) 

    Tam giác ABH vuông tại H nên A^+B^=90° (tổng hai góc nhọn trong một tam giác vuông).

    Suy ra B^=90°−A^=90°−18°=72° 

    Vậy B^=72° tức là toà tháp nghiêng một góc 72° so với phương nằm ngang.

    B. Bài tập

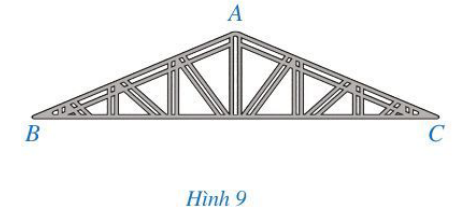
    Bài 1 trang 72 Toán 7 Tập 2: Một khung thép có dạng hình tam giác ABC với số đo các góc ở đỉnh B và đỉnh C cùng bằng 23° (Hình 9). Tính số đo của góc ở đỉnh A.

    Giải Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1) 

    Lời giải

    GT

    Tam giác ABC

    B^=C^=18° 

    KL

    Tính A^.  

    Trong tam giác ABC có A^+B^+C^=180° (tổng ba góc của một tam giác).

    Suy ra A^=180°−B^−C^=180°−23°−23°=134°. 

    Vậy A^=134°. 

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Giải Toán 7 trang 70 Tập 2

    Giải Toán 7 trang 71 Tập 2

    Giải Toán 7 trang 72 Tập 2

    Giải Toán 7 trang 73 Tập 2

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

    Bài 3: Hai tam giác bằng nhau

    Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

    Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

    Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 338 16/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: