Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 107 Tập 2 Cánh diều

    Với giải bài tập Toán lớp 7 trang 107 Tập 2 trong Bài 10: Tính chất ba đường trung tuyến của tam giác sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 107 Tập 2.

    1 1,156 16/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 107 Tập 2

    Bài 1 trang 107 Toán 7 Tập 2: Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:

    GA + GB + GC = 23(AM + BN + CP).

    Lời giải:

    GT

    DABC, ba đường trung tuyến AM, BN, CP đồng quy tại G

    KL

    GA + GB + GC = 23(AM + BN + CP).

    Chứng minh (Hình vẽ dưới đây):

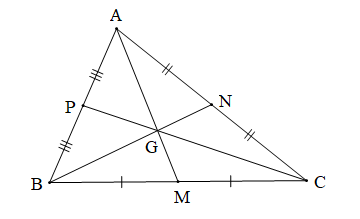
    Giải Toán 7 Bài 10 (Cánh diều): Tính chất ba đường trung tuyến của tam giác (ảnh 1) 

    Tam giác ABC có ba đường trung tuyến AM, BN, CP đồng quy tại G nên G là trọng tâm của tam giác ABC.

    Khi đó AG = 23AM; BG = 23BN; CG = 23CP (tính chất trọng tâm của tam giác)

    Do đó GA + GB + GC = 23AM + 23BN + 23CP = 23(AM + BN + CP).

    Vậy GA + GB + GC = 23(AM + BN + CP).

    Bài 2 trang 107 Toán 7 Tập 2: Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

    a) BM = CN;

    b) ∆GBC cân tại G.

    Lời giải:

    GT

    ∆ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G

    KL

    a) BM = CN;

    b) ∆GBC cân tại G.

    Chứng minh (Hình vẽ dưới đây):

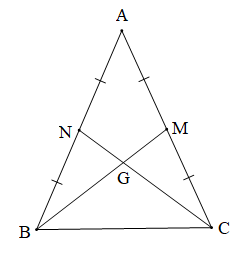
    Giải Toán 7 Bài 10 (Cánh diều): Tính chất ba đường trung tuyến của tam giác (ảnh 1) 

    a) Tam giác ABC cân tại A (giả thiết) nên AB = AC (1).

    Do BM đường trung tuyến của tam giác ABC nên M là trung điểm của AC do đó AM=MC=12AC  (2)

    CN là đường trung tuyến của tam giác ABC nên N là trung điểm của AB do đó AN=NB=12AB  (3)

    Từ (1), (2) và (3) ta có: AM = AN.

    Xét ∆ABM và ∆ACN có:

    AM = AN (chứng minh trên).

    A^ là góc chung,

    AB = AC (chứng minh trên)

    Do đó ∆ABM = ∆ACN (c.g.c)

    Suy ra BM = CN (2 cạnh tương ứng).

    Vậy BM = CN.

    b) Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của tam giác ABC.

    Suy ra BG = 23BM; CG = 23CN (tính chất trọng tâm của tam giác).

    Mà BM = CN (chứng minh câu a)

    Do đó BG = CG.

    Tam giác GBC có BG = CG nên tam giác GBC cân tại G.

    Vậy ∆GBC cân tại G.

    Bài 3 trang 107 Toán 7 Tập 2: Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:

    a) GA = GD;

    b) ∆MBG = ∆MCD;

    c) CD = 2GN.

    Lời giải:

    GT

    ∆ABC, hai đường trung tuyến AM và BN cắt nhau tại G, D ∈ tia đối của tia MA, MD = MG.

    KL

    a) GA = GD;

    b) ∆MBG = ∆MCD;

    c) CD = 2GN.

    Chứng minh (Hình vẽ dưới đây):

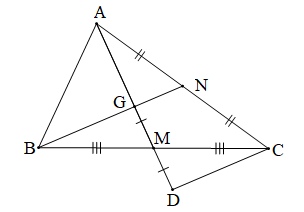
    Giải Toán 7 Bài 10 (Cánh diều): Tính chất ba đường trung tuyến của tam giác (ảnh 1) 

    a) Tam giác ABC có hai đường trung tuyến AM, BN cắt nhau tại G (giả thiết) nên G là trọng tâm của tam giác ABC.

    Khi đó GM = 12GA (tính chất trọng tâm của tam giác).

    Điểm D nằm trên tia đối của tia MA và MD = MG (giả thiết) nên M là trung điểm của GD.

    Suy ra GM = 12GD.

    Do đó GA = GD.

    Vậy GA = GD.

    b) Do M là trung điểm của GD nên MG = MD.

    Xét ∆MBG và ∆MDC có:

    MB = MC (giả thiết),

    GMB^=DMC^ (hai góc đối đỉnh),

    MG = MD (chứng minh trên),

    Do đó ∆MBG = ∆MDC (c.g.c).

    c) Vì ∆MBG = ∆MDC (chứng minh câu b) nên CD = BG (hai cạnh tương ứng).

    Lại có G là trọng tâm của tam giác ABC nên BG = 2GN.

    Do đó CD = 2GN.

    Vậy CD = 2GN.

    Bài 4 trang 107 Toán 7 Tập 2: Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:

    a) ∆AHB = ∆AHM;

    b) AG=23AB.

    Lời giải:

    GT

    ∆ABC

    Hai đường trung tuyến AM và BN cắt nhau tại G,

    H là hình chiếu của A lên đường thẳng BC, H là trung điểm của BM.

    KL

    a) ∆AHB = ∆AHM;

    b) AG=23AB.

    Chứng minh (Hình vẽ dưới đây):

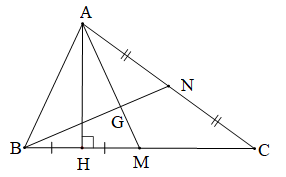
    Giải Toán 7 Bài 10 (Cánh diều): Tính chất ba đường trung tuyến của tam giác (ảnh 1) 

    a) Vì H là hình chiếu của A trên BC nên AH ⊥ BC

    Do đó ∆AHB vuông tại H và ∆AHM vuông tại H.

    Xét ∆AHB (vuông tại H) và ∆AHM (vuông tại H) có:

    AH là cạnh chung,

    HB = HM (H là trung điểm của BM).

    Do đó ∆AHB = ∆AHM (hai cạnh góc vuông).

    Vậy ∆AHB = ∆AHM.

    b) Vì ∆AHB = ∆AHM (chứng minh câu a)

    Nên AB = AM (hai cạnh tương ứng).

    ∆ABC có hai đường trung tuyến AM, BN cắt nhau tại G nên G là trọng tâm của ∆ABC.

    Suy ra AG = 23AM (tính chất trọng tâm của tam giác)

    Do đó AG = 23AB.

    Vậy AG=22AB. 

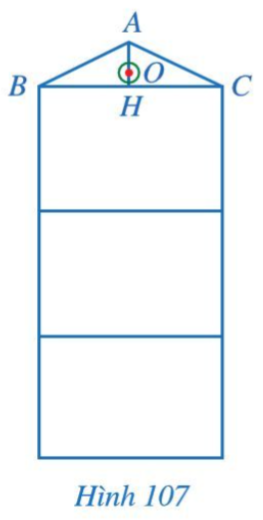
    Bài 5 trang 107 Toán 7 Tập 2: Hình 107 là mặt cắt đứng của một ngôi nhà có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.

    Giải Toán 7 Bài 10 (Cánh diều): Tính chất ba đường trung tuyến của tam giác (ảnh 1) 

    a) AH có vuông góc với BC không? Vì sao?

    b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất?

    Lời giải:

    a) DABC cân tại A nên AB = AC và ABH^=ACH^.

    Lại có AH là đường trung tuyến của ∆ABC nên H là trung điểm của BC.

    Do đó BH = CH.

    Xét ∆ABH và ∆ACH có:

    AB = AC (chứng minh trên),

    ABH^=ACH^ (chứng minh trên),

    BH = CH (chứng minh trên),

    Do đó ∆ABH = ∆ACH (c.g.c).

    Suy ra AHB^=AHC^ (hai góc tương ứng).

    Mà AHB^+AHC^=180° 

    Nên AHB^=AHC^=180°2=90° 

    Hay AH ⊥ BC.

    Vậy AH ⊥ BC.

    b) Vì O là trọng tâm của tam giác ABC nên OH = 13AH (tính chất trong tâm tam giác)

    Mà AH = 1,2 m

    Do đó OH = 13. 1,2 = 0,4 m.

    Vì mỗi tầng cao 3,3 m mà ngôi nhà ba tầng nên vị trí O ở độ cao so với mặt đất là:

    0,4 + 3,3 . 3 = 10,3 (m)

    Vậy vị trí O ở độ cao 10,3 m so với mặt đất.

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Giải Toán 7 trang 104 Tập 2

    Giải Toán 7 trang 105 Tập 2

    Giải Toán 7 trang 106 Tập 2

    Giải Toán 7 trang 107 Tập 2

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 11: Tính chất ba đường phân giác của tam giác

    Bài 12: Tính chất ba đường trung trực của tam giác

    Bài 13: Tính chất ba đường cao của tam giác

    Bài tập cuối chương 7

    Chủ đề 3: Dung tích phổi

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,156 16/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: