Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 57 Tập 1 Chân trời sáng tạo

    Với giải bài tập Toán lớp 10 trang 57 Tập 1 trong Bài 2: Hàm số bậc hai sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 57 Tập 1.

    1 429 21/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 57 Tập 1

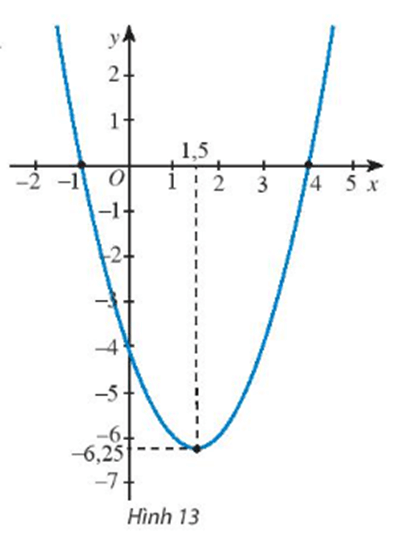
    Bài 8 trang 57 Toán lớp 10 Tập 1: Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.

    Tìm công thức của hàm số bậc hai có đồ thị như Hình 13

    Lời giải:

    Gọi hàm số bậc hai có đồ thị như Hình 13 có dạng là y = ax2 + bx + c (với a, b, c là các số thực, a ≠ 0).

    Đồ thị hàm số cắt trục tung tại điểm (0; –4) nên ta có:

    a.02 + b.0 + c = –4 ⇒ c = –4.

    Đồ thị hàm số cắt trục hoành tại hai điểm (–1; 0) và (4; 0) nên ta có:

    a.(–1)2 + b.(–1) – 4 = 0 ⇒ a – b  = 4  (1)

    a.42 + b.4 – 4 = 0 ⇒ 16a + 4b = 4 (2)

    Từ (1) và (2) ta có hệ phương trình:

    a−b=416a+4b=4⇔a−b=420a=20⇔1−b=4a=1⇔b=−3a=1

    Vậy hàm số bậc hai cần tìm là y = x2 – 3x – 4 .

    Bài 9 trang 57 Toán lớp 10 Tập 1: Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.

    Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:

    - Dây dài nhất là 5m, dây ngắn nhất là 0,8m. Khoảng cách giữa các dây bằng nhau.

    - Nhịp cầu dài 30m.

    - Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

     

    Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol

    Lời giải:

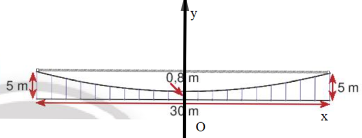
    Giải Toán 10 Bài 2: Hàm số bậc hai - Chân trời sáng tạo (ảnh 1)

    Chọn hệ trục tọa độ như hình vẽ.

    Trong đó, khoảng cách giữa các dây bằng nhau và có 20 khoảng cách nên mỗi khoảng cách ứng với 30 : 20 = 1,5 m.

    Gọi dạng parabol của thành cầu là đồ thị của hàm số y = ax2 + bx + c (a, b, c là các số thực, a ≠ 0).

    Đồ thị hàm số cắt trục tung tại điểm (0; 0,8) nên ta có:

    a.02 + b.0 + c = 0,8 ⇒ c = 0,8

    Tại hai đầu cầu, tức y = 5 thì ta có hai giá trị x thỏa mãn là x1 = –15 và x2 = 15

    Từ đó ta có:

    a.(–15)2 + b.(–15) + 0,8 = 5 ⇒ 225a – 15b = 4,2      (1)

    a.152 + b.15 + 0,8 = 5 ⇒ 225a + 15b = 4,2              (2)

    Từ (1) và (2) ta có hệ phương trình 225a−15b=4,2225a+15b=4,2⇔a=7375b=0 .

    Vậy phương trình parabol cần tìm là: y=7375x2+0,8.

    Độ dài mỗi dây ở vị trí hoành độ tương ứng là:

    Tại x = 0, độ dài dây là: 0,8 + 5%.0,8 = 0,84 (m)

    Tại x = 1,5 và x = –1,5 thì độ dài dây là:

    7375.1,52+0,8+5%.7375.1,52+0,8=0,8841 (m)

    Tại x = 3 và x = –3 thì độ dài dây là:

    7375.32+0,8+5%.7375.32+0,8=1,0164 (m)

    Tại x = 4,5 và x = –4,5 thì độ dài dây là:

    7375.4,52+0,8+5%.7375.4,52+0,8=1,2369 (m)

    Tại x = 6 và x = –6 thì độ dài dây là:

    7375.62+0,8+5%.7375.62+0,8=1,5456 (m)

    Tại x = 7,5 và x = –7,5 thì độ dài dây là:

    7375.7,52+0,8+5%.7375.7,52+0,8=1,9425 (m)

    Tại x = 9 và x = –9 thì độ dài dây là:

    7375.92+0,8+5%.7375.92+0,8=2,4276 (m)

    Tại x = 10,5 và x = –10,5 thì độ dài dây là:

    7375.10,52+0,8+5%.7375.10,52+0,8=3,0009(m)

    Tại x = 12 và x = –12 thì độ dài dây là:

    7375.122+0,8+5%.7375.122+0,8=3,6624(m)

    Tại x = 13,5 và x = –13,5 thì độ dài dây là:

    7375.13,52+0,8+5%.7375.13,52+0,8=4,4121(m)

    Tại x = 15 và x = –15 thì độ dài dây là:

    5 + 5%.5 = 5,25 (m)

    Chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên của cầu là:

    4.(0,84 + 0,8841 + 1,0164 + 1,2369 + 1,5456 + 1,9425 + 2,4276 + 3,0009 + 3,6624 + 4,4121 + 5,25) = 104,874 (m).

    Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên của cầu là: 104,874 m.

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải Toán 10 trang 49 Tập 1

    Giải Toán 10 trang 52 Tập 1

    Giải Toán 10 trang 53 Tập 1

    Giải Toán 10 trang 55 Tập 1

    Giải Toán 10 trang 56 Tập 1

    Giải Toán 10 trang 57 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài tập cuối chương 3

    Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

    Bài 2: Định lí côsin và định lí sin

    Bài 3: Giải tam giác và ứng dụng thực tế

    Bài tập cuối chương 4

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 429 21/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: