Giải Toán 10 trang 18 Tập 2 Chân trời sáng tạo

Giải Toán 10 trang 18 Tập 2

Bài 1 trang 18 Toán lớp 10 Tập 2: Xét dấu của các tam thức bậc hai sau:

a) f(x) = 6x² + 41x + 44;

b) g(x) = - 3x² + x – 1;

c) h(x) = 9x² + 12x + 4.

Lời giải:

a) Tam thức bậc hai f(x) = 6x² + 41x + 44 có ∆ = 41² – 4.6.44 = 625 > 0 và a = 6 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = $-\frac{4}{3}$  và x₂ = $-\frac{11}{2}$ .

Khi đó ta có bảng xét dấu sau:

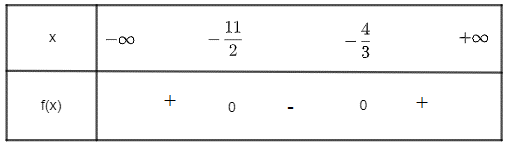
Vậy f(x) âm khi x thuộc khoảng $\left(-\frac{11}{2};-\frac{4}{3}\right)$ , f(x) dương khi x thuộc hai khoảng $\left(-\infty ;-\frac{11}{2}\right)$  và $\left(-\frac{4}{3};+\infty \right)$ .

b) Tam thức bậc hai g(x) = - 3x² + x – 1 có ∆ = 1² – 4.(-3).(-1) = -11 < 0 và a = -3 < 0. Do đó g(x) vô nghiệm. Khi đó ta có bảng xét dấu sau:

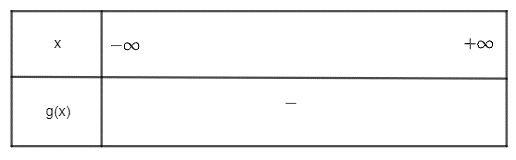
Vậy g(x) âm với mọi x ∈ ℝ.

c) Tam thức bậc hai h(x) = 9x² + 12x + 4 có ∆ = 12² – 4.9.4 = 0 và a = 9 > 0. Do đó h(x) có nghiệm kép x₁ = x₂ = $\frac{-2}{3}$ .

Khi đó ta có bảng xét dấu sau:

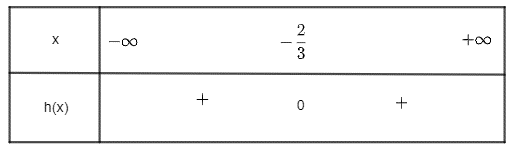
Vậy h(x) dương với mọi x ≠ $\frac{-2}{3}$ .

Bài 2 trang 18 Toán lớp 10 Tập 2: Giải các bất phương trình sau:

a) 7x² – 19x – 6 ≥ 0;

b) – 6x² + 11x > 10;

c) 3x² – 4x + 7 > x² + 2x + 1;

d) x² – 10x + 25 ≤ 0.

Lời giải:

a) Tam thức bậc hai f(x) = 7x² – 19x – 6 có a = 7 > 0 và ∆ = 19² – 4.7.(-6) = 529 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = 3 và x₂ = $-\frac{2}{7}$ .

Suy ra f(x) dương khi x thuộc khoảng $\left(-\infty ;-\frac{2}{7}\right)$  và (3; +∞), f(x) âm khi x thuộc khoảng $\left(-\frac{2}{7};3\right)$  và f(x) = 0 khi x = 3 và x = $-\frac{2}{7}$ .

Vậy bất phương trình đã cho có tập nghiệm là S = $\left(-\infty ;-\frac{2}{7}\right]$  ∪ [3; +∞).

b) Tam thức bậc hai g(x) = – 6x² + 11x – 10 có a = - 6 < 0 và ∆ = 11² – 4.(-6).(-10) = -119 < 0. Do đó g(x) vô nghiệm.

Suy ra g(x) luôn âm với mọi x thuộc ℝ

Vậy bất phương trình đã cho có tập nghiệm là S = $\varnothing$ .

c) Ta có: 3x² – 4x + 7 > x² + 2x + 1

⇔ 2x² – 6x + 6 > 0

Tam thức bậc hai h(x) = 2x² – 6x + 6 có a = 2 > 0 và ∆’ = 3² – 2.6 = - 3 < 0. Do đó h(x) có vô nghiệm.

Suy ra h(x) dương với mọi x thuộc ℝ.

Vậy bất phương trình đã cho có tập nghiệm S = ℝ.

d) Ta có tam thức bậc hai k(x) = x² – 10x + 25 có a = 1 > 0 và ∆’ = 5² – 25 = 0. Do đó k(x) có nghiệm kép x₁ = x₂ = 5.

Suy ra f(x) dương khi x ≠ 5 và f(x) = 0 khi x = 5.

Vậy bất phương trình đã cho có tập nghiệm là S = {5}.

Bài 3 trang 18 Toán lớp 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải thích các bất phương trình sau:

a) x² – 0,5x – 5 ≤ 0

b) – 2x² + x – 1 > 0

Lời giải:

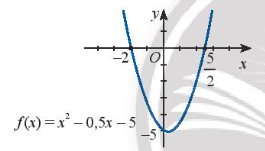
a) Quan sát đồ thị ta thấy:

Với x thuộc hai khoảng (-∞; -2) và $\left(\frac{5}{2};+\infty \right)$  thì đồ thị hàm số nằm phía trên trục hoành. Do đó f(x) > 0 khi x ∈ (-∞; -2) ∪ $\left(\frac{5}{2};+\infty \right)$  .

Với x thuộc $\left(-2;\frac{5}{2}\right)$  thì đồ thị hàm số nằm phía dưới trục hoành. Do đó f(x) < 0 khi x ∈ $\left(-2;\frac{5}{2}\right)$ .

Đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ x = - 2 và x = $\frac{5}{2}$ .

Vậy bất phương trình có tập nghiệm là S = $\left[-2;\frac{5}{2}\right]$ .

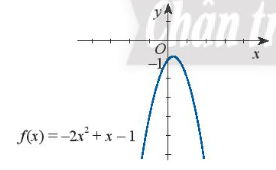
b) Quan sát hình vẽ ta thấy:

Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành với mọi giá trị của x. Do đó f(x) < 0 với mọi x.

Vậy bất phương trình đã cho vô nghiệm.

Bài 4 trang 18 Toán lớp 10 Tập 2: Giải các phương trình sau:

a) $\sqrt{x^2-7x}=\sqrt{-9x^2-8x+3}$ ;

b) $\sqrt{x^2+x+8}-\sqrt{x^2+4x+1}=0$ ;

c) $\sqrt{4x^2+x-1}=x+1$ ;

d) $\sqrt{2x^2-10x-29}=\sqrt{x-8}$ .

Lời giải:

a) $\sqrt{x^2-7x}=\sqrt{-9x^2-8x+3}$

⇒ x² – 7x = - 9x² – 8x + 3

⇒ 10x² + x – 3 = 0

⇒ x = $\frac{1}{2}$  và x =  $-\frac{3}{5}$

Thay lần lượt hai giá trị vào phương trình đã cho ta thấy chỉ có giá trị x = $-\frac{3}{5}$  thỏa mãn.

Vậy tập nghiệm của phương trình đã cho là S = $\left\{-\frac{3}{5}\right\}$ .

b) $\sqrt{x^2+x+8}-\sqrt{x^2+4x+1}=0$

⇒ $\sqrt{x^2+x+8}=\sqrt{x^2+4x+1}$

⇒ x² + x + 8 = x² + 4x + 1

⇒ 3x = 7

⇒ x = $\frac{7}{3}$

Thay x = $\frac{7}{3}$  vào phương trình đã cho ta thấy thỏa mãn.

Vậy tập nghiệm của phương trình là S = $\left\{\frac{7}{3}\right\}$ .

c) $\sqrt{4x^2+x-1}=x+1$

⇒ 4x² + x – 1 = x² + 2x + 1

⇒ 3x² – x – 2 = 0

⇒ x = 1 và x = $-\frac{2}{3}$

Thay lần lượt các giá trị của x vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.

Vậy tập nghiệm của phương trình là S = $\left\{-\frac{2}{3};1\right\}$ .

d) $\sqrt{2x^2-10x-29}=\sqrt{x-8}$

⇒ 2x² – 10x – 29 = x – 8

⇒ 2x² – 11x – 21 = 0

⇒ x = 7 và x = $-\frac{3}{2}$

Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy cả hai giá trị đều không thỏa mãn.

Vậy tập nghiệm của phương trình là S = $\varnothing$ .

Bài 5 trang 18 Toán lớp 10 Tập 2: Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8cm. Tính độ dài cạnh huyền, biết chu vi tam giác 30 cm.

Lời giải:

Không mất tính tổng quát giả sử tam giác cần xét là tam giác vuông tại A có độ dài cạnh AC ngắn hơn cạnh huyền BC 8cm.

Đặt BC = x (cm)

Khi đó AC = x – 8 (cm)

Xét tam giác ABC vuông tại A, có:

BC² = AB² + AC² (định lí Py – ta – go)

⇔ x² = AB² + (x – 8)²

⇔ AB² = x² – (x – 8)²

⇔ AB² = x² – (x² – 16x + 64)

⇔ AB² = 16x – 64

⇔ AB = $\sqrt{16x-64}$  (cm)

Chu vi tam giác ABC là: x + x – 8 + $\sqrt{16x-64}$  = 2x – 8 + $\sqrt{16x-64}$  (cm)

Mà chu vi tam giác bằng 30cm nên có phương trình 2x – 8 + $\sqrt{16x-64}$ = 30

⇒ $\sqrt{16x-64}$ = 38 – 2x 

⇒ 16x – 64 = 1 444 – 152x + 4x²

⇒ 4x² – 168x + 1 508 = 0

⇒ x² – 42x + 377 = 0

⇒ x = 29 và x = 13

Thay lần lượt vào phương trình đã cho ta thấy chỉ có x = 13 thỏa mãn.

Vậy độ dài cạnh huyền bằng 13cm thì tam giác thỏa mãn điều kiện đầu bài.

Bài 6 trang 18 Toán lớp 10 Tập 2: Một quả bóng được bắn thẳng lên độ cao 2m với vận tốc ban đầu là 30m/s. Khoảng cách của quả bóng sau t giây được cho bởi hàm số

h(t) = - 4,9t² + 30t + 2,

với h(t) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 40m trong bao nhiêu lâu? Làm tròn kết quả đến hàng phần mười.

Lời giải:

Quả bóng nằm ở độ cao trên 40m nghĩa là h(t) > 40 hay - 4,9t² + 30t + 2 > 40

⇔ - 4,9t² + 30t – 38 > 0

Tam thức bậc hai f(t) = - 4,9t² + 30t – 38, có a = -4,9 < 0 và ∆’ = 15² – (-4,9).(-38) = $\frac{194}{5}$  > 0. Do đó f(t) có hai nghiệm phân biệt t₁ ≈ 4,3 và t₂ ≈ 1,8.

Khi đó ta có bảng xét dấu:

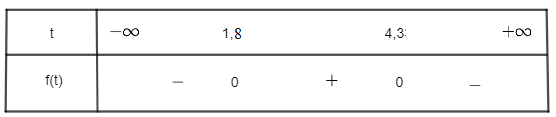
Suy ra f(t) dương khi t thuộc khoảng (1,8; 4,3).

Vậy quả bóng nằm ở độ cao trên 40m trong 4,3 – 1,8 = 2,5 s.

Bài 7 trang 18 Toán lớp 10 Tập 2: Một chú cá heo nhảy lên khỏi mặt nước. Độ cao h(mét) của cá heo với mặt nước sau t giây được cho bởi hàm số:

h(t) = - 4,9t² + 9,6t

Tính khoảng thời gian cá heo ở trên không.

Lời giải:

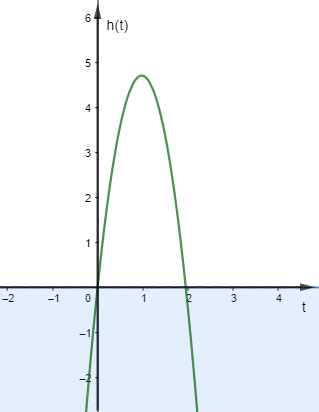
Đặt hệ trục tọa độ như hình vẽ với Ot biểu diễn thời gian (giây) là trục trùng với mặt nước, trục h(t) biểu diễn độ cao (mét), độ cao h(t) = - 4,9t² + 9,6t là hàm bậc hai được biểu diễn bởi đường cong parabol màu xanh trên hình vẽ.

Khoảng thời gian cá heo ở trên không tính từ khi cá heo rời khỏi mặt nước nên chính là phần đồ thị nằm trên trục Ot hay - 4,9t² + 9,6t > 0.

Tam thức bậc hai h(t) = - 4,9t² + 9,6t có a = -4,9 < 0 và ∆ = 9,6² – 4.(-4,9).0 = 92,16 > 0. Do đó h(t) có hai nghiệm phân biệt t₁ = 0 và t₂ = $\frac{96}{49}$

Suy ra h(t) dương khi t thuộc khoảng $\left(0;\frac{96}{49}\right)$ .

Do đó h(t) > 0 khi t ∈ $\left(0;\frac{96}{49}\right)$ .

Vậy khoảng thời gian cá heo ở trên không là $\frac{96}{49}$  giây.

Bài 8 trang 18 Toán lớp 10 Tập 2: Lợi nhuận một tháng p(x) của một quán ăn phụ thuộc vào giá trung bình x của các món ăn theo công thức p(x) = -30x² + 2 100x – 15 000, với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận trung bình không dưới 15 triệu một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào?

Lời giải:

Ta có 15 triệu = 15 000 (nghìn đồng)

Lợi nhuận trung bình không dưới 15 triệu nghĩa là p(x) = -30x² + 2 100x – 15 000 ≥ 15 000

⇔ -30x² + 2 100x – 30 000 ≥ 0

⇔ -x² + 70x – 1 000 ≥ 0

Tam thức bậc hai f(x) = -x² + 70x – 1 000 có a = -1 < 0 và ∆ = 70² – 4.(-1).(-1 000) = 900 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = 50 và x₂ = 20.

Suy ra f(x) dương khi x thuộc khoảng (20; 50).

Do đó bất phương trình f(x) ≥ 0 với x thuộc [20; 50].

Vậy để lợi nhuận trung bình không dưới 15 triệu một tháng thì giá bán trung bình của các món ăn cần có giá từ 20 nghìn đồng đến 50 nghìn đồng.

Bài 9 trang 18 Toán lớp 10 Tập 2: Quỹ đạo của một quả bóng được mô tả bằng hàm số y = f(x) = -0,03x² + 0,4x + 1,5 với y (tính bằng mét) là độ cao của quả bóng so với mặt đất khi độ dịch chuyển theo phương ngang của bóng là x (tính bằng mét). Để quả bóng có thể ném được qua lưới cao 2m, người ném phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười.

Lời giải:

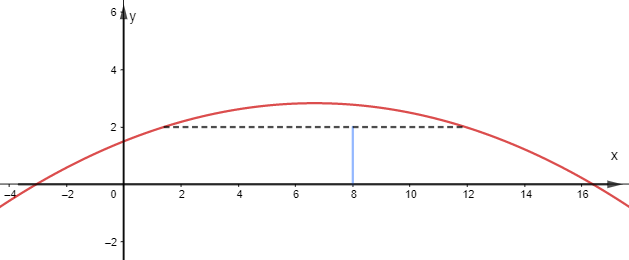
Để quả bóng có thể ném được qua lưới cao 2m nghĩa là -0,03x² + 0,4x + 1,5 > 2

⇔ -0,03x² + 0,4x + 1,5 – 2 > 0

⇔ -0,03x² + 0,4x – 0,5 > 0

Tam thức bậc hai f(x) = -0,03x² + 0,4x – 0,5 có a = -0,03 < 0 và ∆ = 0,4² – 4.(-0.03).(-0,5) = 0,34 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ ≈ 11,9 và x₂ ≈ 1,4.

Suy ra f(x) dương khi x thuộc khoảng (1,4; 11,9).

Vậy để quả bóng có thể ném được qua lưới cao 2m thì người đứng cách lưới ít nhất 1,4m và nhiều nhất là 11,9m.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

Giải Toán 10 trang 18 Tập 2

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

Bài 1: Quy tắc cộng và quy tắc nhân

Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Bài 3: Nhị thức Newton

Bài tập cuối chương 8

Bài 1: Tọa độ của vectơ