Nội dung bài viết

    Xem thêm

    Bài 2 trang 78 Toán 7 Tập 2 | Chân trời sáng tạo Giải Toán lớp 7

    Lời giải Bài 2 trang 78 Toán 7 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 842 28/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 Chân trời sáng tạo Bài 8: Tính chất ba đường cao của tam giác

    Bài 2 trang 78 Toán 7 Tập 2:

    Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.

    Lời giải:

    GT

    ∆ABC vuông tại A;

    M thuộc tia BA, BM = BC;

    AH là tia phân giác của góc B, H ∈ AC.

    KL

    MH ⊥ BC.

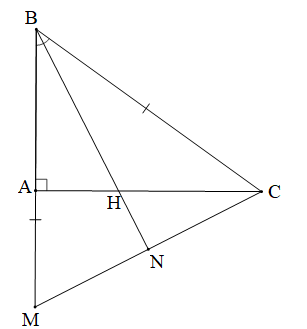
    Giải Toán 7 Bài 8 (Chân trời sáng tạo): Tính chất ba đường cao của tam giác (ảnh 1) 

    Gọi N là giao điểm của BH và MC.

    Xét ∆BMN và ∆BCN có:

    BM = BC (giả thiết),

    MBN^=CBN^ (do BN là tia phân giác của góc B),

    BN là cạnh chung,

    Do đó ∆BMN = ∆BCN (c.g.c)

    Suy ra BNM^=BNC^ (hai góc tương ứng)

    Mà BNM^+BNC^=180° (hai góc kề bù)

    Nên BNM^=BNC^=180o2=90o hay BN ⊥ MC.

    Tam giác BMC có CA ⊥ BM (do CA ⊥ BA), BN ⊥ MC (chứng minh trên)

    Do đó CA, BN là hai đường cao của tam giác BMC.

    Mà CA và BN cắt nhau tại H nên H là trực tâm của tam giác BMC.

    Do đó MH ⊥ BC.

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Khởi động trang 77 Toán 7 Tập 2: Làm thế nào để tính khoảng cách từ mỗi đỉnh đến cạnh đối diện của một tam giác...

    Khám phá 1 trang 77 Toán 7 Tập 2: Em hãy vẽ một tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh đối diện AC...

    Thực hành 1 trang 77 Toán 7 Tập 2: Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC...

    Vận dụng 1 trang 77 Toán 7 Tập 2: Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a)...

    Khám phá 2 trang 77 Toán 7 Tập 2: Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao...

    Thực hành 2 trang 78 Toán 7 Tập 2: Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6).Chứng minh rằng NS vuông góc với ML...

    Vận dụng 2 trang 78 Toán 7 Tập 2: Cho tam giác ABC có ba đường cao AD, BE, CF đồng quy tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC...

    Bài 1 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M...

    Bài 2 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H...

    Bài 3 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE...

    Bài 4 trang 78 Toán 7 Tập 2: Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều...

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 7: Tính chất ba đường trung tuyến của tam giác

    Bài 8: Tính chất ba đường cao của tam giác

    Bài 9: Tính chất ba đường phân giác của tam giác

    Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học

    Bài tập cuối chương 8

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 842 28/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: