Sách bài tập Toán 8 Bài 3 (Chân trời sáng tạo): Các trường hợp đồng dạng của hai tam giác vuông
Với giải sách bài tập Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 3.
Giải SBT Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
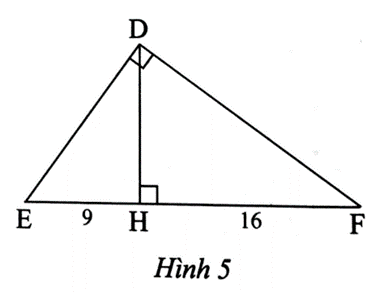
Bài 1 trang 68 SBT Toán 8 Tập 2: Quan sát Hình 5.
a) Chứng minh rằng ∆HDE ᔕ ∆HFD.
Lời giải:
a) Xét ∆HDE vuông tại H và ∆HFD vuông tại H có
(cùng phụ với ).
Do đó ∆HDE ᔕ ∆HFD (g.g).
b) Ta có ∆HDE ᔕ ∆HFD, suy ra .
Do đó HD2 = HE.HF = 9.16 = 144, suy ra HD = 12.
Vậy HD = 12.
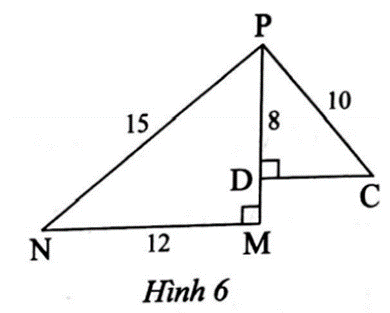
Bài 2 trang 68 SBT Toán 8 Tập 2: Quan sát Hình 6, chứng minh rằng:
Lời giải:
a) Ta có và .
Xét ∆MNP vuông tại M và ∆DPC vuông tại D có .
Do đó ∆MNP ᔕ ∆DPC.
b) Ta có ∆MNP ᔕ ∆DPC, suy ra .
Mà (∆MNP vuông tại M).
Do đó , suy ra NP ⊥ PC.
Lời giải:
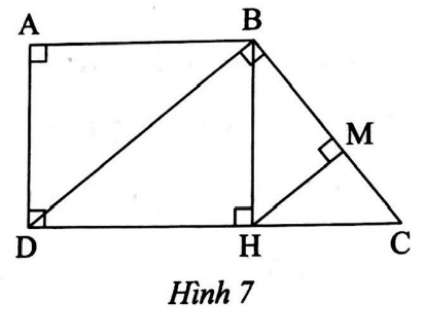
a) Xét ∆ABD vuông tại A và ∆BDC vuông tại B có (so le trong).
Do đó ∆ABD ᔕ ∆BDC (g.g).
Suy ra . Do đó BD2 = BD . DC.
b) Ta có ∆BMH vuông tại M và ∆BHC vuông tại H có chung.
Do đó ∆BMH ᔕ ∆BHC (g.g).
Suy ra . Do đó BH2 = BM . BC.
Tứ giác ABHD là hình chữ nhật, suy ra AD = BH.
Vậy AD2 = BM . BC.
Lời giải:
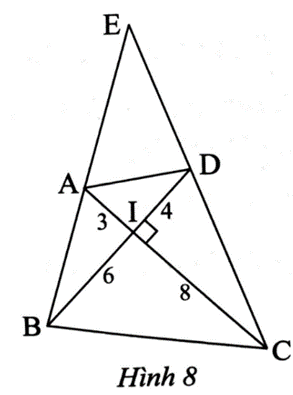
a) Ta có ; suy ra .
Xét ∆AIB vuông tại I và ∆DIC vuông tại I có .
Suy ra ∆AIB ᔕ ∆DIC
b) Ta có ∆AIB ᔕ ∆DIC, suy ra .
Xét ∆EDB và ∆EAC có
chung và .
Do đó ∆EDB ᔕ ∆EAC (g.g).
Suy ra . Do đó EA . EB = EC . ED (đpcm).
a) Chứng minh rằng ∆ABH ᔕ ∆MNK. Tính tỉ số .
b) Biết diện tích tam giác ABC bằng 56 cm2. Tính diện tích tam giác MNP.
Lời giải:
a) Ta có ∆ABC ᔕ ∆MNP, suy ra
Xét ∆ABH vuông tại H và ∆MNK vuông tại K có .
Do đó ∆ABH ᔕ ∆MNK (g.g).
Suy ra .
Vậy .
b) Ta có ∆ABC ᔕ ∆MNP, suy ra hay .
Do đó (cm2).
Vậy diện tích tam giác MNP là 126 cm2.
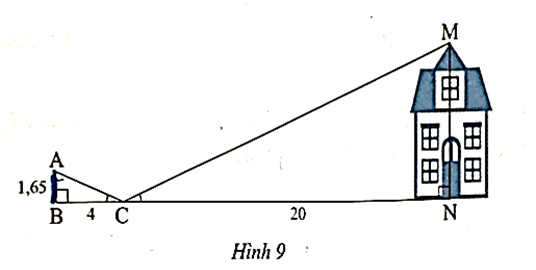
Lời giải:
Xét ∆ABC vuông tại B và ∆MNC vuông tại N có .
Do đó ∆ABC ᔕ ∆MNC (g.g).
Suy ra hay .
Do đó (m).
Vậy chiều cao MN của căn nhà là 8,25 m.
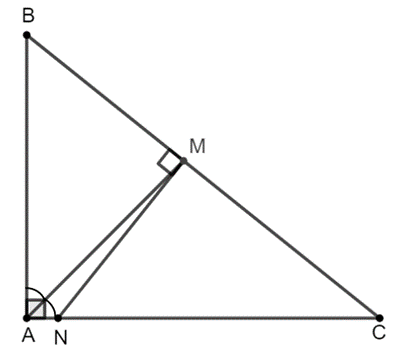
b) MN = MB.
Lời giải:
a) Xét ∆MNC vuông tại M và ∆ABC vuông tại A có chung.
Do đó ∆MNC ᔕ ∆ABC (g.g).
b) Ta có ∆MNC ᔕ ∆ABC, suy ra (1)
Xét ∆ABC có AM là phân giác của có
, suy ra (2)
Từ (1) và (2), suy ra .
Do đó MN = MB (đpcm).
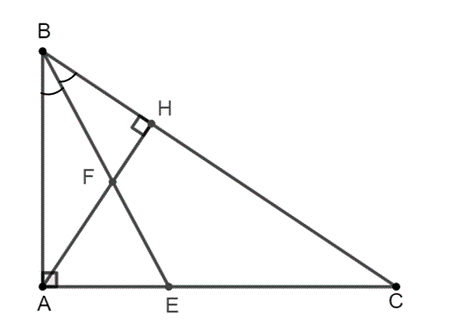
c) AE2 = EC . FH.
Lời giải:
a) Vì BE là tia phân giác của nên .
Xét ∆ABE vuông tại A và ∆HBF vuông tại H có
()
Do đó ∆ABE ᔕ ∆HBF (g.g)
Suy ra . Do đó AB . HF = AE . HB (đpcm).
b) Ta có ∆ABE ᔕ ∆HBF.
Suy ra hay (các góc tương ứng).
Mà (đối đỉnh) nên . Suy ra ∆AEF cân tại A.
Do đó AE = AF.
c) Xét ∆ABC có BE là tia phân giác của , suy ra (1)
Xét ∆ABH có BF là tia phân giác của , suy ra (2)
Xét ∆ABH vuông tại H và ∆ABC vuông tại A có chung.
Do đó ∆ABH ᔕ ∆CBA, suy ra (3)
Từ (1); (2) và (3) suy ra .
Do đó AE . AF = EC . FH.
Mà AE = AF, suy ra AE2 = EC . FH (đpcm).
Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài tập cuối chương 8 trang 73
Bài 1: Mô tả xác suất bằng tỉ số
Xem thêm các chương trình khác:
- Soạn văn lớp 8 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 8 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 8 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 8 - Chân trời sáng tạo
- Giải SBT Ngữ văn 8 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Soạn văn 8 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 8 – Friends Plus
- Giải sbt Tiếng Anh 8 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 8 Friends plus đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 8 Friends plus đầy đủ nhất
- Giải sgk Khoa học tự nhiên 8 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 8 – Chân trời sáng tạo
- Giải sgk Lịch sử 8 – Chân trời sáng tạo
- Lý thuyết Lịch sử 8 - Chân trời sáng tạo
- Giải sbt Lịch sử 8 – Chân trời sáng tạo
- Giải sgk Địa lí 8 – Chân trời sáng tạo
- Lý thuyết Địa lí 8 - Chân trời sáng tạo
- Giải sbt Địa lí 8 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 8 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sgk Công nghệ 8 – Chân trời sáng tạo
- Lý thuyết Công nghệ 8 - Chân trời sáng tạo
- Giải sbt Công nghệ 8 – Chân trời sáng tạo
- Giải sgk Tin học 8 – Chân trời sáng tạo
- Lý thuyết Tin học 8 - Chân trời sáng tạo
- Giải sbt Tin học 8 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 8 – Chân trời sáng tạo