Sách bài tập Toán 8 Bài 2 (Chân trời sáng tạo): Tứ giác
Với giải sách bài tập Toán 8 Bài 2: Tứ giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 2.
Giải SBT Toán 8 Bài 2: Tứ giác
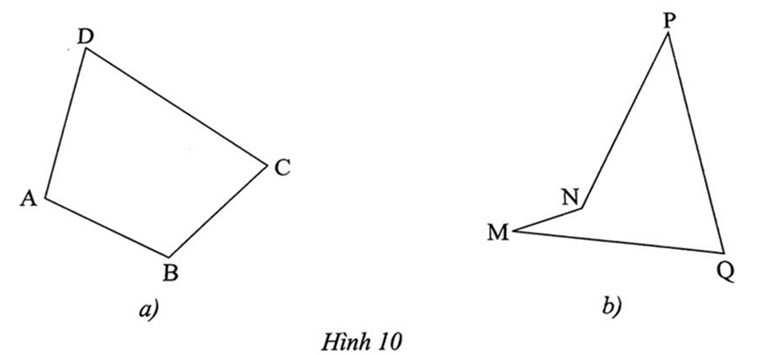
Bài 1 trang 56 SBT Toán 8 Tập 1: Tìm tứ giác lồi trong các hình sau:
Lời giải:
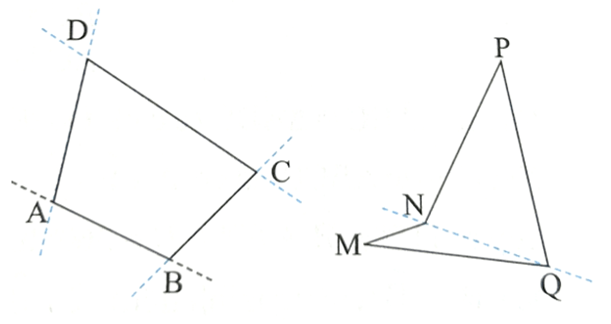
a) Tứ giác ABCD luôn nằm trong cùng một phần mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác nên ABCD là tứ giác lồi.
b) Đường thẳng đi qua cạnh của tứ giác MNPQ chia tứ giác thành hai phần nên MNPQ không phải là tứ giác lồi.
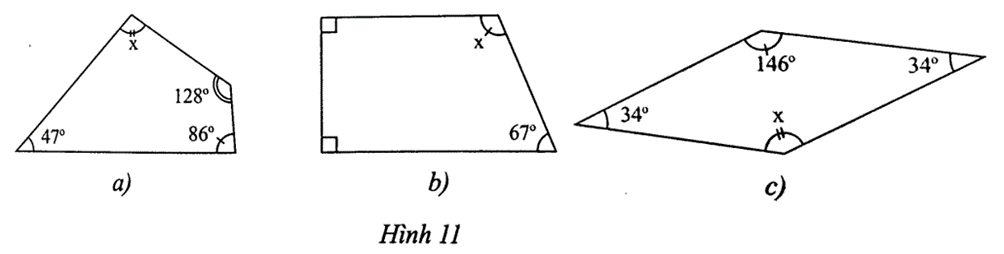
Bài 2 trang 57 SBT Toán 8 Tập 1: Tìm số đo x trong các tứ giác sau:
Lời giải:
Vì tổng số đo các góc của một tứ giác bằng 360° nên ta có:
a) x + 47° + 86° + 128° = 360°
Suy ra x = 360° ‒ (47° + 86° + 128°) = 99°.
b) x + 90° + 90° + 67° = 360°
Suy ra x = 360° ‒ (90° + 90° + 67°) = 113°.
c) x + 34° + 146° + 34° = 360°
Suy ra x = 360° ‒ (34° + 146° + 34°) = 146°.
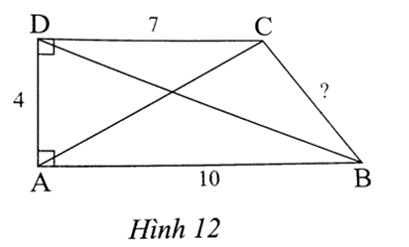
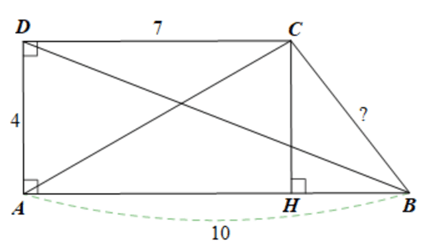
Bài 3 trang 57 SBT Toán 8 Tập 1: Cho tứ giác ABCD như Hình 12.
a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.
b) Cho biết góc B bằng 53°. Tìm số đo góc C.
Lời giải:
a) Áp dụng định lý Pythagore trong tam giác ABD vuông tại A có:
BD2 = AD2 + AB2 = 42 + 102 = 116
Suy ra BD=√116.
Áp dụng định lý Pythagore trong tam giác ADC vuông tại D có:
AC2 = AD2 + DC2 = 42 + 72 = 65
Suy ra AC=√65.
Kẻ CH ⊥ AB (H ∈ AB), mà AD ⊥ AB nên CH // AD
Ta cũng có DC ⊥AD và AB ⊥ AD nên DC // AB
Suy ra ^DCA=^HAC,^DAC=^HCA (các cặp góc so le trong)
Xét ∆ADC và ∆CHA có:
^DCA=^HAC cạnh AC chung, ^DAC=^HCA
Do đó ∆ADC = ∆CHA (g.c.g)
Suy ra: CD = AH, AD = CH
Mà CD = 7, AD = 4 nên AH = 7, CH = 4
Ta có: BH = AB ‒ AH = 10 ‒ 7 =3.
Áp dụng định lý Pythagore trong tam giác CBH vuông tại H có:
BC2 = CH2 + BH2 = 32 + 42 = 25
Suy ra BC=√25=5.
b) Vì tổng số đo các góc của một tứ giác bằng 360° nên trong tứ giác ABCD có:
ˆA+ˆB+ˆC+ˆD=360°
Suy ra .
Lời giải:
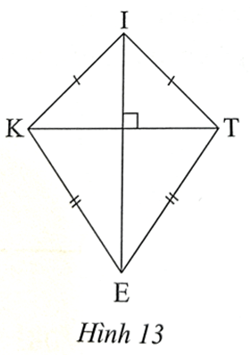
Xét ∆KIE và ∆TIE có:
IK = IT, EK = ET, cạnh IE chung
Do đó ∆KIE = ∆TIE (c.c.c), suy ra (hai góc tương ứng)
Vì tổng số đo các góc của một tứ giác bằng 360° nên trong tứ giác KITE ta có:
, mà (chứng minh trên)
Suy ra
Do đó .
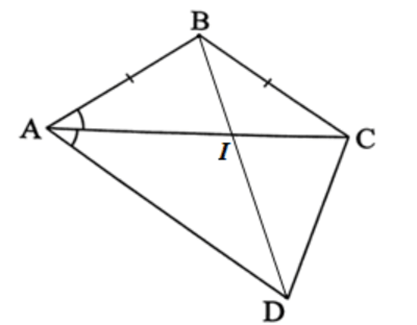
Lời giải:
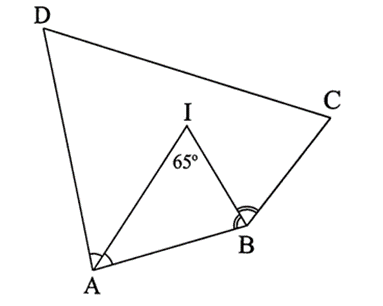
Xét ∆AIB, ta có:
Mà suy ra .
Do AI, BI lần lượt là tia phân giác của nên ta có:
Do đó .
Xét tứ giác
Suy ra .
Mặt khác nên
Thay vào ta có:
Suy ra, .
Do đó .
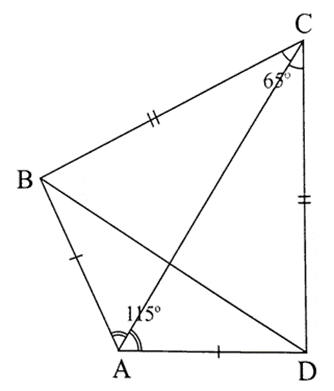
Bài 6 trang 57 SBT Toán 8 Tập 1: Cho tứ giác ABCD có AB = AD, CB = CD, .
a) Chứng minh AC là đường trung trực của BD.
Lời giải:
a) Ta có:
AB = AD (giả thiết), suy ra A thuộc đường trung trực của BD;
CB = CD (giả thiết), suy ra C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ABC và∆ADC, ta có:
AB = AD (giả thiết); BC = DC (giả thiết); AC là cạnh chung.
Suy ra ∆ABC= ∆ADC (c.c.c).
Do đó (hai góc tương ứng)
Xét tứ giác ABCD, ta có .
Hay
Do đó .
Mà (chứng minh trên) nên .
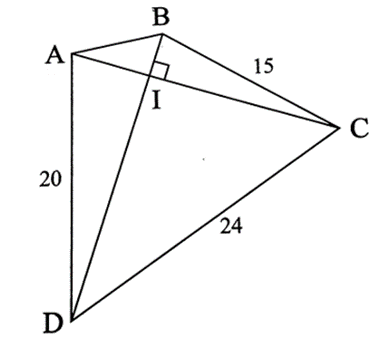
Lời giải:
Áp dụng định lí Pythagore vào bốn tam giác AIB, BIC, CID, DIA vuông tại I, ta có:
AB2 = IA2 + IB2
BC2 = IB2 + IC2
CD2 = IC2 + ID2
AD2 = IA2 + ID2
Nên AB2 + CD2 = IA2 + IB2 + IC2 + ID2
Hay AB2 + CD2 = (IB2 + IC2) + (IA2 + ID2)
AB2 + CD2 = BC2 + AD2
AB2 + 242 = 152 + 202
AB2 = 225 + 400 – 576 = 49
Suy ra (cm).
Lời giải:
Vẽ tứ giác ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.
Theo bất đẳng thức tam giác, ta có:
IA + IB > AB (trong tam giác IAB)
IB + IC > BC (trong tam giác IBC)
IC + ID > CD (trong tam giác ICD)
IA + ID > AD (trong tam giác IAD)
Suy ra2(IA + IB + IC + ID) > AB + BC + CD + DA
Hay 2(AC + BD) > AB + BC + CD + DA
Vậy hay tổng độ dài hai đường chéo của một tứ giác lớn hơn nửa chu vi của tứ giác đó.
Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Hình thang – Hình thang cân
Bài 4: Hình bình hành – Hình thoi
Xem thêm các chương trình khác:
- Soạn văn lớp 8 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 8 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 8 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 8 - Chân trời sáng tạo
- Giải SBT Ngữ văn 8 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Soạn văn 8 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 8 – Friends Plus
- Giải sbt Tiếng Anh 8 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 8 Friends plus đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 8 Friends plus đầy đủ nhất
- Giải sgk Khoa học tự nhiên 8 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 8 – Chân trời sáng tạo
- Giải sgk Lịch sử 8 – Chân trời sáng tạo
- Lý thuyết Lịch sử 8 - Chân trời sáng tạo
- Giải sbt Lịch sử 8 – Chân trời sáng tạo
- Giải sgk Địa lí 8 – Chân trời sáng tạo
- Lý thuyết Địa lí 8 - Chân trời sáng tạo
- Giải sbt Địa lí 8 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 8 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sgk Công nghệ 8 – Chân trời sáng tạo
- Lý thuyết Công nghệ 8 - Chân trời sáng tạo
- Giải sbt Công nghệ 8 – Chân trời sáng tạo
- Giải sgk Tin học 8 – Chân trời sáng tạo
- Lý thuyết Tin học 8 - Chân trời sáng tạo
- Giải sbt Tin học 8 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 8 – Chân trời sáng tạo