Sách bài tập Toán 8 (Chân trời sáng tạo) Bài tập cuối chương 8 trang 73
Với giải sách bài tập Toán 8 Bài tập cuối chương 8 trang 73 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8.
Giải SBT Toán 8 Bài tập cuối chương 8 trang 73
CÂU HỎI TRẮC NGHIỆM
A. 1k;
B. 1k2;
C. k ;
D. k2.
Lời giải:
Đáp án đúng là: C
Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số của chu vi của hai tam giác đó bằng k.
B. 32;
C. 94;
D. 49.
Lời giải:
Đáp án đúng là: B
Nếu ∆ABC ᔕ ∆MNP theo tỉ số k=23 thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số 1k=32.
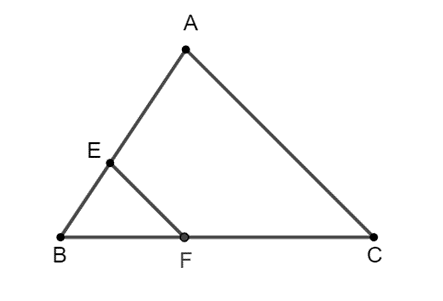
Bài 3 trang 73 SBT Toán 8 Tập 2: Nếu tam giác ABC có EF // AC (với E ∈ AB; F ∈ BC) thì:
B. ∆FBE ᔕ ∆CAB;
C. ∆EBF ᔕ ∆ABC;
D. ∆BFE ᔕ ∆BAC.
Lời giải:
Đáp án đúng là: C
Xét ∆BEF và ∆ABC có
ˆB chung và ^BEF=^BAC (EF // AC, hai góc đồng vị).
Do đó ∆EBF ᔕ ∆ABC (g.g).
B. 12 cm;
C. 16 cm;
D. 24 cm.
Lời giải:
Đáp án đúng là: A
Ta có ∆ABD ᔕ ∆DEF với tỉ số đồng dạng k=34.
Suy ra ADDF=34 hay AD12=34.
Do đó AD=3.124=9 (cm).
Vậy AD = 9 cm.
Bài 5 trang 73 SBT Toán 8 Tập 2: Nếu tam giác ABC và tam giác DEF có ˆA=ˆD; ˆC=ˆF thì:
C. ∆ACB ᔕ ∆DFE;
D. ∆CBA ᔕ ∆FDE.
Lời giải:
Đáp án đúng là: C
Nếu tam giác ABC và tam giác DEF có ˆA=ˆD; ˆC=ˆF thì ∆ACB ᔕ ∆DFE.
B. 6,4 cm;
C. 22,5 cm;
D. 10 cm.
Lời giải:
Đáp án đúng là: B
Ta có ∆MNP ᔕ ∆EFG, suy ra MNEF=NPFG hay 8EF=1512.
Do đó EF=8.1215=6,4 (cm).
Vậy EF = 6,4 cm.
Bài 7 trang 73 SBT Toán 8 Tập 2: Cho ∆ABC ᔕ ∆XYZ, biết ˆY=75°; . Khi đó số đo bằng:
B. 69°;
C. 36°;
D. 75°.
Lời giải:
Đáp án đúng là: B
Ta có ∆ABC ᔕ ∆XYZ, suy ra và .
Xét ∆ABC có .
Suy ra .
Vậy .
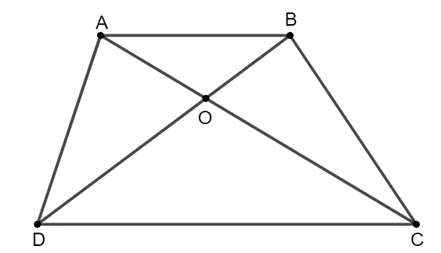
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là: C
∆AOB ᔕ ∆COD với tỉ số đồng dạng .
BÀI TẬP TỰ LUẬN
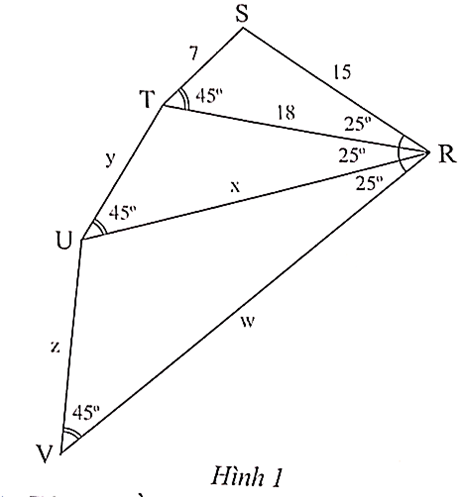
Bài 1 trang 74 SBT Toán 8 Tập 2: Cho Hình 1. Tính x, y, z, w.
Lời giải:
• Xét ∆STR và ∆TUR có:
và
Do đó ∆STR ᔕ ∆TUR (g.g).
Suy ra hay .
Suy ra và .
Vậy x = 21,6 và y = 8,4.
• Xét ∆STR và ∆UVR có:
và
Do đó ∆STR ᔕ ∆UVR (g.g).
Suy ra hay .
Suy ra và .
Do đó và .
Vậy x = 21,6 ; y = 8,4 ; z = 10,08 và w = 25,92.
Lời giải:
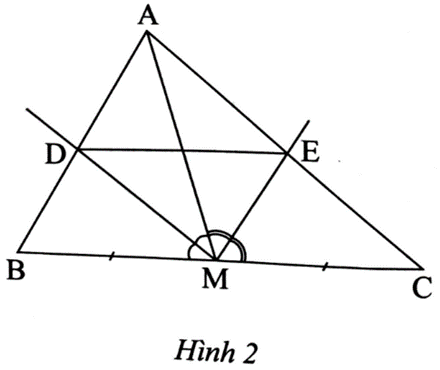
• Vì MD là tia phân giác của nên .
• Vì ME là tia phân giác của nên .
Vì AM là đường trung tuyến nên MB = MC .
Do đó . Suy ra DE // BC.
Suy ra ∆ADE ᔕ ∆ABC.
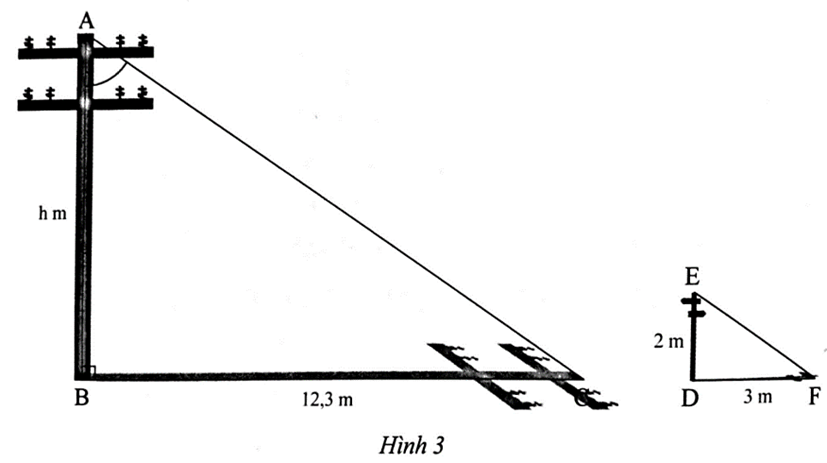
Bài 3 trang 74 SBT Toán 8 Tập 2: Tính chiều cao cột điện AB trong Hình 3.
Lời giải:
Ta có ∆ABC ᔕ ∆EDF, suy ra hay .
Do đó .
Vậy chiều cao cột điện AB là 8,2 m.
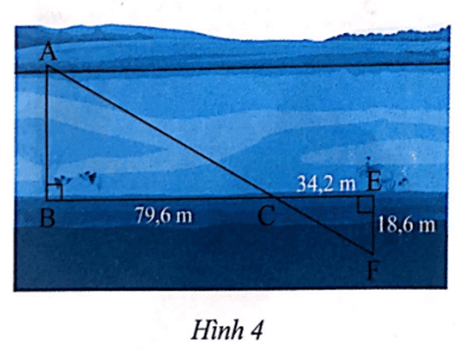
Bài 4 trang 74 SBT Toán 8 Tập 2: Tính khoảng cách AB của một khúc sông trong Hình 4.
Lời giải:
Xét ∆ABC vuông tại A và ∆FEC vuông tại E có (đối đỉnh).
Do đó ∆ABC ᔕ ∆FEC (g.g).
Suy ra hay .
Do đó (m).
Vậy khoảng cách AB của một khúc sông là 43,29 m.
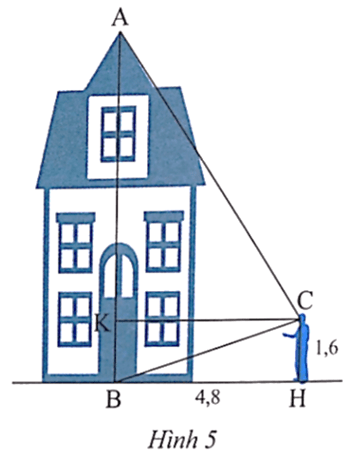
Lời giải:
Ta có ∆AKC ᔕ ∆BHC (g.g), suy ra hay .
Do đó .
Độ cao của toà nhà cao là:
14,4 + 1,6 = 16 (m).
Vậy độ cao của toà nhà cao là 16 m.
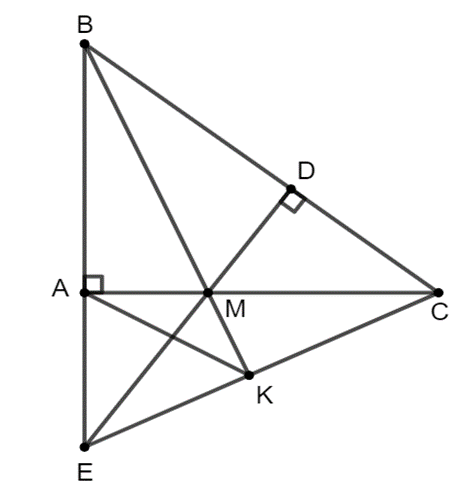
a) Chứng minh rằng ∆DMC ᔕ ∆ABC.
b) Gọi E là giao điểm của đường thẳng AB với đường thẳng MD.
Chứng minh rằng DB . DC = DE . DM.
c) Đường thẳng BM cắt EC tại K. Chứng minh rằng .
Lời giải:
a) Xét ∆DMC vuông tại D và ∆ABC vuông tại A có chung.
Do đó ∆DMC ᔕ ∆ABC (g.g).
b) Xét ∆DBE vuông tại D và ∆DMC vuông tại D có
(cùng phụ với ).
Do đó ∆DBE ᔕ ∆DMC (g.g).
Suy ra . Do đó DB . DC = DE . DM (đpcm).
c) Xét ∆BEC có đường cao CA và BE cắt nhau tại M, suy ra M là trực tâm ∆BEC.
Do đó BK ⊥ EC.
Xét ∆EAC vuông tại A và ∆EKB vuông tại K có chung.
Do đó ∆EAC ᔕ ∆EKB (g.g)
Suy ra hay .
Xét ∆EAK và ∆ECB có và chung.
Do đó ∆EAK ᔕ ∆ECB (c.g.c).
Suy ra (các góc tương ứng).
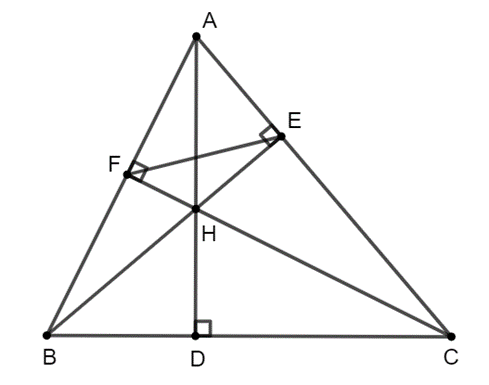
b) HA . HD = HB . HE = HC . HF.
c) BC2 = BE . BH + CF . CH.
Lời giải:
a) Ta có (cùng phụ với ).
Mà (đối đỉnh) nên .
Xét ∆ADC vuông tại D và ∆BDH vuông tại D có .
Do đó ∆ADC ᔕ ∆BDH (g.g).
Suy ra . Do đó AD . BH = AC . BD (đpcm).
b) Xét ∆HEA vuông tại E và ∆HDB vuông tại D có (đối đỉnh).
Do đó ∆HEA ᔕ ∆HDB (g.g).
Suy ra . Do đó HA . HD = HB . HE (1)
Xét ∆HFA vuông tại F và ∆HDC vuông tại D có (đối đỉnh).
Do đó ∆HFA ᔕ ∆HDC (g.g).
Suy ra . Do đó HA . HD = HC . HF (2)
Từ (1) và (2) suy ra HA . HD = HB . HE = HC . HF (đpcm).
c) Xét ∆BEC vuông tại E và ∆BHD vuông tại D có chung.
Do đó ∆BEC ᔕ ∆BHD (g.g).
Suy ra . Do đó BC . BD = BE . BH (3)
Xét ∆BCF vuông tại F và ∆HCD vuông tại D có chung.
Do đó ∆BCF ᔕ ∆HCD (g.g)
Suy ra . Do đó BC . DC = CF . HC. (4)
Từ (3) và (4), suy ra BC . DB + BC . DC = BE . BH + CF . HC.
Do đó BC2 = BE . BH + CF . CH (đpcm).
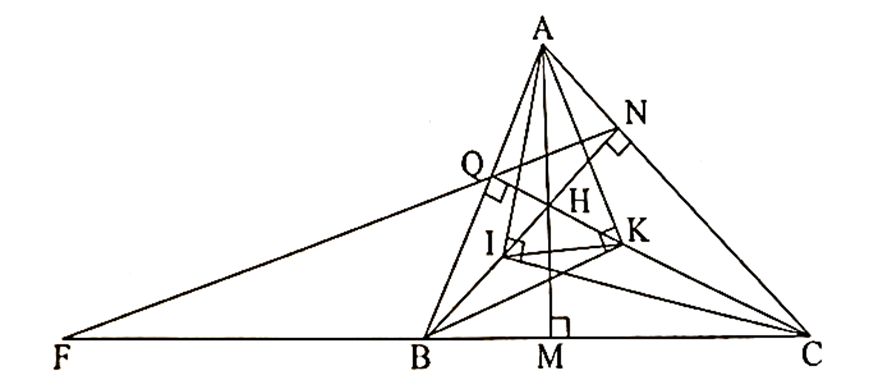
Bài 8 trang 75 SBT Toán 8 Tập 2: Cho tam giác nhọn ABC có ba đường cao AM, BN, CQ cắt nhau tại H.
a) Chứng minh rằng ∆ANQ ᔕ ∆ABC.
b) Đường thẳng QN cắt đường thẳng BC tại F. Chứng minh rằng FB . FC = FQ . FN.
c) Trên đoạn HB lầy điểm I sao cho . Chứng minh rằng AI2 = AN . AC.
d) Trên đoạn HC lấy điểm K sao cho . Chứng mình rằng ∆AIK cân.
Lời giải:
a) Xét ∆ANB vuông tại N và ∆AQC vuông tại Q có chung.
Do đó ∆ANB ᔕ ∆AQC (g.g).
Suy ra hay .
Xét ∆ANQ và ∆ABC có
; chung.
Do đó ∆ANQ ᔕ ∆ABC (c.g.c)
b) Xét ∆FQB và ∆FCN có
chung; .
Do đó ∆FQB ᔕ ∆FCN (g.g).
Suy ra . Do đó FB . FC = FQ . FN (g.g).
c) Xét ∆ANI vuông tại N và ∆AIC vuông tại I có chung.
Do đó ∆ANI ᔕ ∆AIC (g.g).
Suy ra . Do đó AI2 = AN . AC (1)
d) Xét ∆AQK vuông tại Q và ∆AKB vuông tại K có chung.
Do đó ∆AQK ᔕ ∆AKB (g.g).
Suy ra . Do đó AK2 = AQ . AB (2)
Mà nên suy ra AN . AC = AQ . AB (3)
Từ (1), (2) và (3) suy ra AI = AK.
Vậy nên ∆AIK cân tại A.
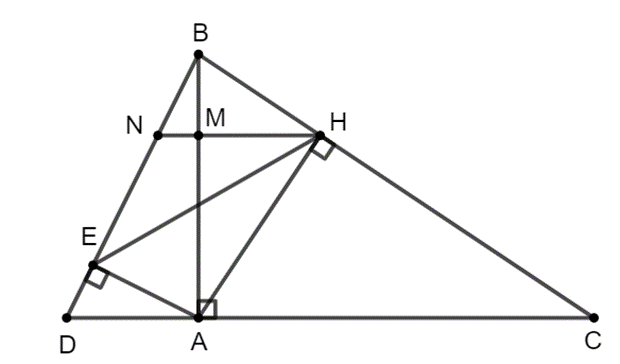
Bài 9 trang 75 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A và đường cao AH.
a) Chứng mình rằng AB2 = BH . BC.
b) Chứng mỉnh rằng AH2 = BH . CH.
c) Trên tia đối của tia AC lấy điểm D (AD < AC). Đường thẳng qua H và song song với AC cắt AB, BD lần lượt tại M, N. Chứng minh rằng .
d) Vẽ AE vuông góc với BD tại E. Chứng minh rằng .
Lời giải:
a) Xét ∆ABC vuông tại A và ∆HBA vuông tại H có chung.
Do đó ∆ABC ᔕ ∆HBA (g.g).
Suy ra . Do đó AB2 = BC . BH (đpcm).
b) Xét ∆HBA vuông tại H và ∆HAC vuông tại H có
(cùng phụ với ).
Do đó ∆HBA ᔕ ∆HAC (g.g).
Suy ra . Do đó AH2 = BH . CH (đpcm).
c) Xét ∆ABD có MN // AD, suy ra (1)
Xét ∆ABC có MH // AC, suy ra (2)
Từ (1) và (2) suy ra . Do đó (đpcm).
d) Xét ∆ABD vuông tại A và ∆EBA vuông tại E có chung.
Do đó ∆ABD ᔕ ∆EBA (g.g).
Suy ra . Do đó AB2 = BD . BE.
Mà AB2 = BC . BH nên BC . BH = BD . BE.
Do đó .
Xét ∆BEH và ∆BCD có
và chung.
Do đó ∆BEH ᔕ ∆BCD (c.g.c).
Suy ra (hai góc tương ứng).
Mà (cùng phụ với ).
Do đó (đpcm).
Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
Bài 1: Mô tả xác suất bằng tỉ số
Xem thêm các chương trình khác:
- Soạn văn lớp 8 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 8 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 8 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 8 - Chân trời sáng tạo
- Giải SBT Ngữ văn 8 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Soạn văn 8 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 8 – Friends Plus
- Giải sbt Tiếng Anh 8 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 8 Friends plus đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 8 Friends plus đầy đủ nhất
- Giải sgk Khoa học tự nhiên 8 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 8 – Chân trời sáng tạo
- Giải sgk Lịch sử 8 – Chân trời sáng tạo
- Lý thuyết Lịch sử 8 - Chân trời sáng tạo
- Giải sbt Lịch sử 8 – Chân trời sáng tạo
- Giải sgk Địa lí 8 – Chân trời sáng tạo
- Lý thuyết Địa lí 8 - Chân trời sáng tạo
- Giải sbt Địa lí 8 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 8 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sgk Công nghệ 8 – Chân trời sáng tạo
- Lý thuyết Công nghệ 8 - Chân trời sáng tạo
- Giải sbt Công nghệ 8 – Chân trời sáng tạo
- Giải sgk Tin học 8 – Chân trời sáng tạo
- Lý thuyết Tin học 8 - Chân trời sáng tạo
- Giải sbt Tin học 8 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 8 – Chân trời sáng tạo