Sách bài tập Toán 8 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 26

Giải SBT Toán 8 Bài tập cuối chương 1 trang 26

A. Câu hỏi trắc nghiệm

Câu 1 trang 26 SBT Toán 8 Tập 1: Bậc của đơn thức 2x²y(2y²)² là

A. 2.

B. 5.

C. 8.

D. 7.

Lời giải:

Đáp án đúng là: D

Ta có: 2x²y(2y²)² = 2x²y.4y⁴ = 8x²y⁵, bậc của 8x²y⁵ là 7.

Câu 2 trang 26 SBT Toán 8 Tập 1: Kết quả của phép nhân (4x – y)(y + 4x) là

A. 16x² – y².

B. y² – 16x².

C. 4x² – y².

D. 16x² – 8xy + y².

Lời giải:

Đáp án đúng là: A

Ta có: (4x – y)(y + 4x) = (4x – y)(4x + y) = (4x)² ‒ y² = 16x² – y².

Câu 3 trang 26 SBT Toán 8 Tập 1: Thực hiện phép nhân (a² – 2a + 4)(a + 2), ta nhận được

A. a³ – 8.

B. a³ + 8.

C. (a – 2)³.

D. (a + 2)³.

Lời giải:

Đáp án đúng là: B

Ta có:

(a² – 2a + 4)(a + 2)

= (a + 2)(a² – 2.a + 2²)

= a³ + 2³

= a³ + 8.

Câu 4 trang 26 SBT Toán 8 Tập 1: Phân tích đa thức 16x² – y⁴ thành nhân tử, ta nhận được

A. (4x² – y²)(4x² + y²).

B. x²(2 – y)(2 + y)(4x + y²).

C. (y² + 4x)(y² – 4x).

D. (4x – y²)(4x + y²).

Lời giải:

Đáp án đúng là: D

Ta có: 16x² – y⁴ = (4x)² ‒ (y²)² = (4x ‒ y²)(4x + y²).

Câu 5 trang 26 SBT Toán 8 Tập 1: Phân tích đa thức x²(x + 1) – x(x + 1) thành nhân tử, ta nhận được

A. x.

B. x(x + 1).

C. x(x – 1)(x + 1).

D. x(x + 1)².

Lời giải:

Đáp án đúng là: C

Ta có: x²(x + 1) – x(x + 1) = (x + 1)(x² ‒ x) = x(x + 1)(x ‒1).

Câu 6 trang 26 SBT Toán 8 Tập 1: Phân tích đa thức 5x – 5y + ax – ay thành nhân tử, ta nhận được

A. (5 + a)(x – y).

B. (5 – a)(x + y).

C. (5 + a)(x + y).

D. 5(x – y + a).

Lời giải:

Đáp án đúng là: A

Ta có: 5x – 5y + ax – ay = (5x – 5y) + (ax – ay)

= 5(x ‒ y) + a(x ‒ y) = (x ‒ y)(5 + a).

Câu 7 trang 26 SBT Toán 8 Tập 1: Rút gọn phân thức $\frac{a\left(7-b\right)}{b\left(b^2-49\right)}$,ta nhận được

A. $\frac{a}{b\left(b-7\right)}$.

B. $\frac{a}{b\left(b+7\right)}$.

C. $-\frac{a}{b\left(b+7\right)}$.

D. $\frac{a}{b\left(7-b\right)}$.

Lời giải:

Đáp án đúng là: C

Ta có: $\frac{a\left(7-b\right)}{b\left(b^2-49\right)}=\frac{-a\left(b-7\right)}{b\left(b-7\right)\left(b+7\right)}=\frac{-a}{b\left(b+7\right)}$.

Câu 8 trang 26 SBT Toán 8 Tập 1: Kết quả của phép trừ $\frac{a^2+2ab}{a-2b}-\frac{6ab-4b^2}{a-2b}$ là

A. a + 2b.

B. a – 2b.

C. 2.

D. $\frac{a^2-4ab-4b^2}{a-2b}$.

Lời giải:

Đáp án đúng là: B

Ta có: $\frac{a^2+2ab}{a-2b}-\frac{6ab-4b^2}{a-2b}=\frac{a^2+2ab-\left(6ab-4b^2\right)}{a-2b}$

$=\frac{a^2+2ab-6ab+4b^2}{a-2b}=\frac{a^2-4ab+4b^2}{a-2b}$

$=\frac{{\left(a-2b\right)}^2}{a-2b}=a-2b$.

Câu 9 trang 26 SBT Toán 8 Tập 1: Kết quả của phép trừ $\frac{2b}{a^2+ab}-\frac{2a}{b^2+ab}$ là

A. $\frac{2\left(a+b\right)}{ab}$.

B. $\frac{2\left(a^2+b^2\right)}{ab}$.

C. $\frac{2\left(a-b\right)}{ab}$.

D. $\frac{2\left(b-a\right)}{ab}$.

Lời giải:

Đáp án đúng là: D

Ta có: $\frac{2b}{a^2+ab}-\frac{2a}{b^2+ab}=\frac{2b}{a\left(a+b\right)}-\frac{2a}{b\left(a+b\right)}$

$=\frac{2b.b-2a.a}{ab\left(a+b\right)}=\frac{2b^2-2a^2}{ab\left(a+b\right)}$

$=\frac{2\left(b-a\right)\left(b+a\right)}{ab\left(a+b\right)}=\frac{2\left(b-a\right)}{ab}$.

Câu 10 trang 26 SBT Toán 8 Tập 1: Kết quả của phép chia $\frac{x^2-y^2}{6xy}:\frac{x-y}{3y}$ là

A. $\frac{x+y}{2x}$.

B. $\frac{x+y}{18x}$.

C. $\frac{2\left(x+y\right)}{x}$.

D. $\frac{x+y}{18x{y}^2}$.

Lời giải:

Đáp án đúng là: A

Ta có: $\frac{x^2-y^2}{6xy}:\frac{x-y}{3y}=\frac{x^2-y^2}{6xy}.\frac{3y}{x-y}$

$=\frac{\left(x-y\right)\left(x+y\right)}{6xy}.\frac{3y}{x-y}=\frac{x+y}{2x}$.

B. Bài tập tự luận

Bài 11 trang 27 SBT Toán 8 Tập 1: Thu gọn các đa thức sau:

a) ab(3a – 2b) – ab(3b – 2a);

b) (a – 4b)(a + 2b) + a(a + 2b).

Lời giải:

a) Cách 1:

ab(3a – 2b) – ab(3b – 2a)

= 3a²b – 2ab² – 3ab² + 2a²b

= (3a²b + 2a²b) + (– 2ab² – 3ab²)

= 5a²b – 5ab².

Cách 2:

ab(3a – 2b) – ab(3b – 2a)

= ab[(3a ‒ 2b) ‒ (3b ‒ 2a)]

= ab(3a ‒ 2b ‒ 3b + 2a)

= ab(5a ‒ 5b) = 5a²b ‒ 5ab².

b) Cách 1:

(a – 4b)(a + 2b) + a(a + 2b)

= a(a + 2b) – 4b(a + 2b) + a² + 2ab

= a² + 2ab – 4ab – 8b² + a² + 2ab

= (a² + a²) + (2ab – 4ab + 2ab) – 8b²

= 2a² – 8b².

Cách 2:

(a – 4b)(a + 2b) + a(a + 2b)

= (a + 2b)(a ‒ 4b + a)

= (a + 2b)(2a ‒ 4b)

= 2(a + 2b)(a ‒ 2b)

= 2[a² ‒ (2b)²] = 2(a² – 4b²)

= 2a² ‒ 8b².

Bài 12 trang 27 SBT Toán 8 Tập 1: Thu gọn các biểu thức sau:

a) (a – 4)(a + 4) + (2a – 1)²;

b) (3a – b)² – (a – 2b)(2b – a).

Lời giải:

a) (a – 4)(a + 4) + (2a – 1)²

= a² ‒ 4² + (2a)² ‒2.2a + 1

= a² ‒ 16 + 4a² ‒ 4a + 1

= (a² + 4a²) ‒ 4a ‒16 + 1

= 5a² ‒ 4a ‒ 15.

b) (3a – b)² – (a – 2b)(2b – a)

= (3a – b)² – [‒(a – 2b)(a ‒ 2b)]

= (3a)²‒2.3a.b + b² + (a ‒ 2b)²

= 9a² ‒ 6ab + b² + a² ‒ 4ab + 4b²

= (9a² + a²) + (‒6ab ‒ 4ab) + (b² + 4b²)

= 10a² ‒ 10ab + 5b².

Bài 13 trang 27 SBT Toán 8 Tập 1: Thực hiện các phép nhân sau:

a) (x + y + 1)(x + y – 1);

b) (x + y – 4)(x – y + 4).

Lời giải:

a) Cách 1:

(x + y + 1)(x + y – 1)

= x(x + y – 1) + y(x + y – 1) + (x + y – 1)

= x² + xy ‒ x + xy + y² ‒ y + x + y ‒ 1

= x² + y² + (xy + xy) + (‒x + x) + (‒y + y) ‒1

= x² + y² + 2xy ‒ 1.

Cách 2:

(x + y + 1)(x + y – 1)

= (x + y)² – 1

= x² + 2xy + y² – 1.

b) Cách 1:

(x + y – 4)(x – y + 4)

= x(x – y + 4) + y(x – y + 4) – 4(x – y + 4)

= x² ‒ xy + 4x + xy ‒ y² + 4y ‒ 4x + 4y ‒16

= x² ‒y² +(‒xy + xy) + (4x ‒ 4x) + (4y + 4y) ‒16

= x² ‒y² + 8y ‒16.

Cách 2:

(x + y – 4)(x – y + 4)

= [x + (y – 4)].[x – (y – 4)]

= x² – (y – 4)²

= x² – (y² – 8y + 16)

= x² ‒y² + 8y ‒16.

Bài 14 trang 27 SBT Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 3(a – b) + 2(a – b)²;

b) (a + 2)² – (4 – a²);

c) a² – 2ab – 4a + 8b;

d) 9a² – 4b² + 4b – 1;

e) a²b⁴ – 81a²;

g) a⁶ – 1.

Lời giải:

a) 3(a – b) + 2(a – b)²

= (a ‒ b)[3 + 2(a ‒ b)]

= (a ‒ b)(3 + 2a ‒ 2b).

b) (a + 2)² – (4 – a²)

= (a + 2)²‒ (2 ‒ a)(2 + a)

= (a + 2)[(a + 2) ‒ (2 ‒ a)]

= (a + 2)(a + 2 ‒ 2 + a)

= 2a(a + 2).

c) a² – 2ab – 4a + 8b

= (a² – 2ab) – (4a ‒ 8b)

= a(a ‒ 2b) ‒ 4(a ‒ 2b)

= (a ‒ 2b)(a ‒ 4).

d) 9a² – 4b² + 4b – 1

= 9a² – (4b² – 4b + 1)

= (3a)² – (2b – 1)²

= (3a + 2b – 1)(3a – 2b + 1).

e) a²b⁴ – 81a²

= a²(b⁴ ‒ 81)

= a²[(b²)² ‒ 9²]

= a²(b² + 9)(b² ‒ 9)

= a²(b² + 9)(b² ‒3²)

= a²(b² + 9)(b ‒ 3)(b + 3).

g) a⁶ – 1

= (a³)² ‒ 1²

= (a³ ‒ 1)(a³ + 1)

= (a ‒ 1)(a² + a + 1)(a + 1)(a² ‒ a + 1).

Bài 15 trang 27 SBT Toán 8 Tập 1: Tính:

a) $\left(a+1+\frac{1-2a^2}{a-1}\right):\left(1-\frac{1}{1-a}\right)$;

b) $\left(\frac{a}{b^2}-\frac{1}{a}\right):\left(\frac{1}{b}+\frac{1}{a}\right)$;

c) $\left(a-\frac{4ab}{a+b}+b\right).\left(a+\frac{4ab}{a-b}-b\right)$;

d) $ab+\frac{ab}{a+b}\left(\frac{a+b}{a-b}-a-b\right)$.

Lời giải:

a) $\left(a+1+\frac{1-2a^2}{a-1}\right):\left(1-\frac{1}{1-a}\right)$

$=\frac{(a+1)(a-1)+1-2a^2}{a-1}:\frac{1-a-1}{1-a}$

$=\frac{a^2-1+1-2a^2}{a-1}:\frac{-a}{1-a}$

$=\frac{-a^2}{a-1}.\frac{1-a}{-a}$

$=\frac{-a^2}{a-1}.\frac{a-1}{a}=-a$.

b) $\left(\frac{a}{b^2}-\frac{1}{a}\right):\left(\frac{1}{b}+\frac{1}{a}\right)$

$=\frac{a^2-b^2}{a{b}^2}:\frac{a+b}{ab}=\frac{\left(a+b\right)(a-b)}{a{b}^2}.\frac{ab}{a+b}$

$=\frac{\left(a+b\right)(a-b)ab}{a{b}^2\left(a+b\right)}=\frac{a-b}{b}$.

c) $\left(a-\frac{4ab}{a+b}+b\right).\left(a+\frac{4ab}{a-b}-b\right)$

$=\left(\frac{a\left(a+b\right)}{a+b}-\frac{4ab}{a+b}+\frac{b(a+b)}{a+b}\right).\left(\frac{a(a-b)}{a-b}+\frac{4ab}{a-b}-\frac{b(a-b)}{a-b}\right)$

$=\frac{a^2+ab-4ab+ab+b^2}{a+b}.\frac{a^2-ab+4ab-ab+b^2}{a-b}$

$=\frac{a^2-2ab+b^2}{a+b}.\frac{a^2+2ab+b^2}{a-b}$

$=\frac{{\left(a-b\right)}^2{\left(a+b\right)}^2}{(a+b)(a-b)}=(a+b)(a-b)=a^2-b^2$.

d) $ab+\frac{ab}{a+b}\left(\frac{a+b}{a-b}-a-b\right)$

$=ab+\frac{ab}{a+b}\left(\frac{a+b}{a-b}-\left(a+b\right)\right)$

$=ab+\frac{ab}{a+b}.\frac{a+b}{a-b}-\frac{ab}{a+b}.\left(a+b\right)$

$ab+\frac{ab}{a-b}-ab=\frac{ab}{a-b}$.

Bài 16 trang 27 SBT Toán 8 Tập 1: Ở hình bên, độ dài các cạnh AB, BC và GH đã được cho theo a và b; hai cạnh CD và EF bằng nhau; ba cạnh AH, GF và ED bằng nhau.

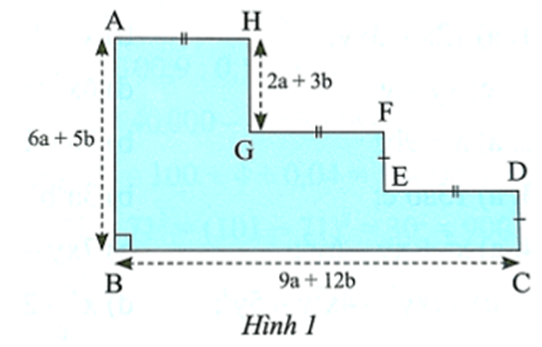
a) Tìm độ dài các cạnh AH, GF, ED.

b) Tìm độ dài các cạnh CD, EF.

c) Tính chu vi của hình bên.

Lời giải:

a) Ta có: AH = GF = ED và AH + GF + ED = BC

Nên $AH=GF=ED=\frac{BC}{3}=\frac{9a+12b}{3}=\frac{3(3a+4b)}{3}=3a+4b$.

b) Ta có:

EF + CD = AB ‒ GH

= 6a + 5b ‒ (2a + 3b) = 6a + 5b ‒ 2a ‒ 3b = 4a + 2b.

Mà EF = CD nên $EF=CD=\frac{4a+2b}{2}=\frac{2(2a+b)}{2}=2a+b$.

c) Chu vi hình vẽ là:

AB + BC + CD + DE + EF + FG + GH + HA

= AB + BC + (CD + EF + GH) + (DE + FG + HA)

= AB + BC + AB + BC

= 2AB + 2BC

= 2(6a + 5b) + 2(9a + 12b)

= 12a + 10b + 18a + 24b

= 30a + 34b.

Bài 17 trang 27 SBT Toán 8 Tập 1: Lúc đầu người ta dự kiến thiết kế một chiếc hộp hình lập phương với độ dài mỗi cạnh là x (cm) (x > 3). Sau đó người ta điều chỉnh tăng chiều 3 cm, giảm chiều rộng 3 cm và giữ nguyên chiều cao. Sau khi điều chỉnh, thể tích của hộp giảm bao nhiêu, diện tích toàn phần của hộp giảm bao nhiêu so với dự kiến ban đầu? Áp dụng với x = 15 cm.

Lời giải:

Theo dự kiến, thể tích và diện tích toàn phần của hộp hình lập phương lần lượt là:

V = x³ (cm³); S = 6x² (cm²).

Sau khi điều chỉnh, hộp cso dạng hình hộp chữ nhật và có:

• Chiều dài là: x + 3 (cm).

• Chiều rộng là: x – 3 (cm).

• Thể tích là: V’ = (x + 3)(x ‒3)x = x(x² ‒ 9) = x³ – 9x (cm³).

• Diện tích một mặt đáy là: S_đáy = (x + 3)(x – 3) = x² – 9 (cm²).

• Diện tích xung quanh là:

S_xq = 2(x + 3 + x – 3).x = 2.2x.x = 4x² (cm²).

• Diện tích toàn phần là:

S’ = S_xq + 2S_đáy = 4x² + 2(x² – 9) = 4x² + 2x² – 18 = 6x² – 18 (cm²).

Từ đó, V ‒ V’ = x³ – (x³ ‒ 9x) = x³ – x³ + 9x = 9x (cm³).

Và S ‒ S’ = 6x² – (6x² ‒ 18) = 6x² ‒ 6x² + 18 = 18 (cm²).

Vậy sau khi điều chỉnh, thể tích của hộp giảm 9x (cm³) và diện tích toàn phần của hộp giảm 18 cm² so với dự kiến ban đầu.

Với x = 15, ta có:

V ‒ V’= 9.15 = 135 (cm³); S ‒ S’ = 18 (cm²).

Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hình chóp tam giác đều

Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Bài tập cuối chương 2 trang 44

Bài 1: Định lí Pythagore

Bài 2: Tứ giác