Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 8 Bài 1 (Chân trời sáng tạo): Định lí Thalès trong tam giác

    Với giải sách bài tập Toán 8 Bài 1: Định lí Thalès trong tam giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 1.

    1 678 30/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 1: Định lí Thalès trong tam giác

    Bài 1 trang 41 SBT Toán 8 Tập 2: Trên một đường thẳng, đặt ba đoạn thẳng liên tiếp AB = BC = CD.

    Tìm tỉ số ABBD; ABAD; ACAD.

    Lời giải:

    Trên một đường thẳng, đặt ba đoạn thẳng liên tiếp AB = BC = CD

    Đặt AB = BC = CD = a, ta có:

    • ABBD=ABBC+CD=aa+a=a2a=12;

    • ABAD=ABAB+BC+CD=aa+a+a=a3a=13;

    • ACAD=AB+BCAB+BC+CD=a+aa+a+a=2a3a=23.

    Bài 2 trang 42 SBT Toán 8 Tập 2: Cho đoạn thẳng AB có độ dài bằng 10 cm. Lấy điểm C thuộc đoạn thẳng AB sao cho CACB=32. Lấy D thuộc tia đối của tia BA sao cho DADB=32.

    Tính độ dài:

    a) CB;

    b) DB;

    c) CD.

    Lời giải:

    Cho đoạn thẳng AB có độ dài bằng 10 cm. Lấy điểm C thuộc đoạn thẳng AB

    a) Ta có CACB=32, suy ra: CA3=CB2.

    Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

    CA3=CB2=CA+CB3+2=AB5=105 = 2.

    Nên CB2 = 2 => CB = 2.2 = 4 (cm).

    b) Ta có DADB=32, suy ra DA3=DB2.

    Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

    DA3=DB2=DA−DB3−2=AB1=101 = 10.

    Nên DB2 = 10 => DB = 10.2 = 20 (cm).

    c) Ta có CD = CB + BD = 4 + 20 = 24 (cm).

    Bài 3 trang 42 SBT Toán 8 Tập 2: Trong Hình 10, cho biết QR // NP và MQ = 10 cm, QN = 5 cm, RP = 6 cm. Tính độ dài MR.

    Trong Hình 10, cho biết QR // NP và MQ = 10 cm, QN = 5 cm, RP = 6 cm

    Lời giải:

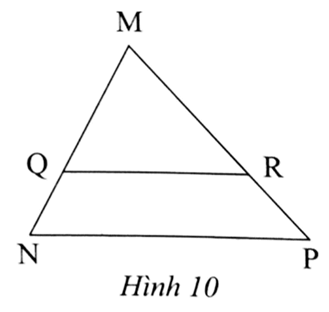
    Xét ∆MNP, có QR // NP, nên theo định lí Thalès, ta có MQQN=MRRP.

    Suy ra MR = MQ.RPQN=10.65 = 12 (cm).

    Vậy MR = 12 cm.

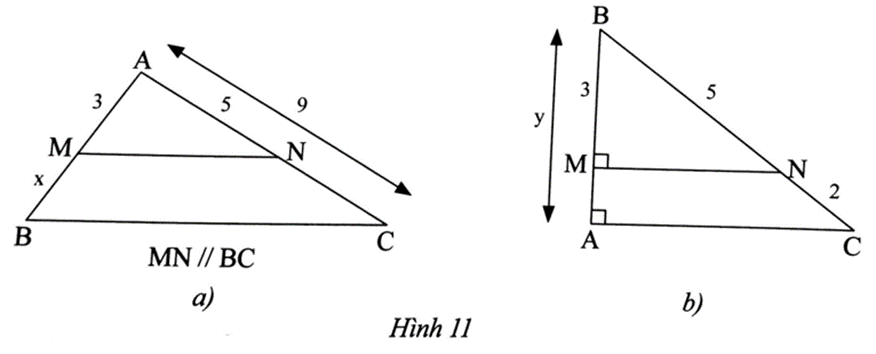
    Bài 4 trang 42 SBT Toán 8 Tập 2: Tính các độ dài x, y trong Hình 11.

    Tính các độ dài x, y trong Hình 11

    Lời giải:

    a) Ta có CN = AC – AN = 9 – 5 = 4.

    Xét ∆ABC, có MN // BC, nên theo định lí Thalès, ta có AMBM=ANCN.

    Suy ra BM = AM.CNAN=3.45 = 2,4.

    Vậy x = 2,4.

    b) ) Ta có BC = BN + NC = 5 + 2 = 7.

    Vì MN và AC cùng vuông góc với AB nên MN song song với AC.

    Xét ∆ABC, có MN // AC, nên theo định lí Thalès, ta có BMAB=BNBC.

    Suy ra AB = BM.BCBN=3.75 = 4,2.

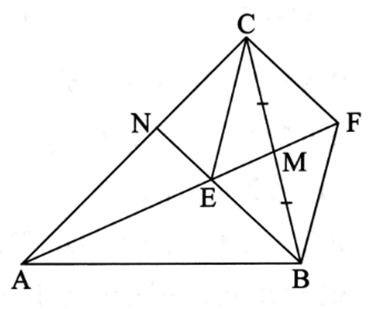
    Bài 5 trang 42 SBT Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến (M ∈ BC). Lấy điểm E thuộc AM sao cho AE = 3EM. Tia BE cắt AC tại N. Tính tỉ số ANNC.

    Lời giải:

    Cho tam giác ABC có AM là đường trung tuyến (M ∈ BC). Lấy điểm E thuộc AM

    Lấy điểm F trên tia AM sao cho M là trung điểm của EF.

    Tứ giác MEFC có hai hai đường chéo BC và EF cắt nhau tại trung điểm của mỗi đường nên tứ giác MEFC là hình bình hành.

    Suy ra CF // BE và CF // EN.

    Ta có AE = 3EM và ME = MF (vì M là trung điểm của EF).

    Khi đó, AEEF=32.

    Xét ∆ACF có CF // EN nên theo định lí Thalès, ta có: ANNC=AEEF=32.

    Vậy ANNC=32.

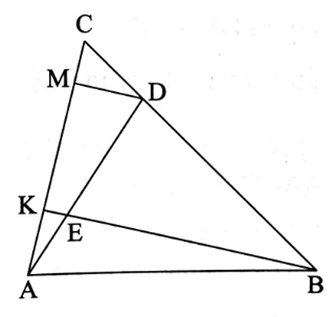
    Bài 6 trang 42 SBT Toán 8 Tập 2: Cho tam giác ABC và điểm D trên cạnh BC sao cho BDBC=34, điểm E trên đoạn AD sao cho AEAD=13. Gọi K là giao điểm của BE và AC. Tính tỉ số AKKC.

    Cho tam giác ABC và điểm D trên cạnh BC sao cho BD/BC = 3/4, điểm E trên đoạn AD

    Lời giải:

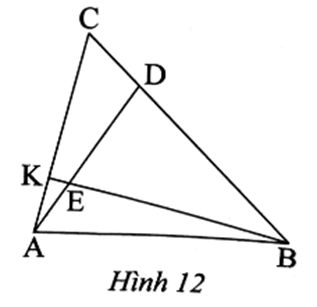
    Cho tam giác ABC và điểm D trên cạnh BC sao cho BD/BC = 3/4, điểm E trên đoạn AD

    Kẻ DM // BK (I ∈ AC)

    Ta có AEAD=13, suy ra AE = 13AD.

    Mặt khác AE + ED = AD, nên ED = 23AD.

    Suy ra AEED=12.

    • Xét ∆ADI có DM // EK (vì DI // BK ) nên theo định lí Thalès, ta có

    AKKM=AEED=12.

    • Xét ∆KBC có DM // BK nên theo định lí Thalès, ta có

    KMKC=BDBC=34.

    Do đó AKKC=AKKI⋅KIKC=12⋅34=38.

    Vậy AKKC=38.

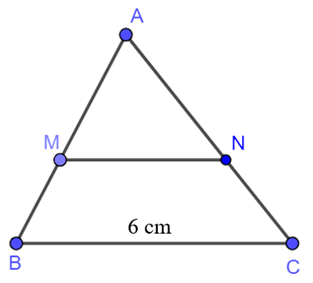
    Bài 7 trang 42 SBT Toán 8 Tập 2: Cho tam giác ABC và điểm M trên cạnh AB sao cho AMMB=32. Kẻ MN // BC (N ∈ AC). Cho biết BC = 6 cm, tính độ dài MN.

    Lời giải:

    Cho tam giác ABC và điểm M trên cạnh AB sao cho AM/MB = 3/2. Kẻ MN // BC

    Ta có AMMB=32, nên AMAB=AMMB+AM=32+3=35.

    Xét ∆ABC có MN // BC, theo hệ quả của định lí Thalès, ta có

    MNBC=AMAB=35.

    Mà BC = 6 cm suy ra MN = 3.65 = 3,6 (cm).

    Vậy MN = 3,6 cm.

    Bài 8 trang 42 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A và MN // BC (M ∈ AB; N ∈ AC). Cho biết AB = 9 cm, AM = 3 cm, AN = 4 cm. Tính độ dài NC, MN, BC.

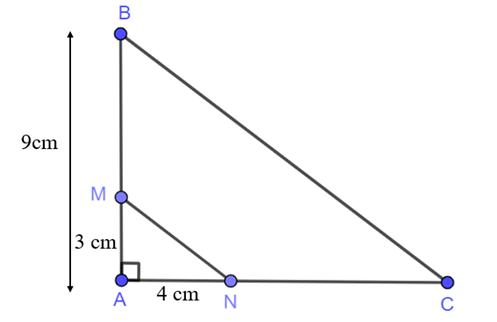
    Lời giải:

    Cho tam giác ABC vuông tại A và MN // BC (M thuộc AB; N thuộc AC)

    Ta có BM = AB – AM = 9 – 3 = 6 (cm)

    Xét ∆ABC có MN // BC nên theo định lí Thalès, ta có AMBM=ANNC.

    Suy ra NC = AN.BMAM=4.63 = 8 (cm)

    Xét ∆AMN vuông tại A, áp dụng định lý Pythagore, ta có:

    MN2 = AM2 + AN2 = 32 + 42 = 25.

    Do đó MN = 5 cm.

    Xét ∆ABC có MN // BC, theo hệ quả của định lí Thalès, ta có MNBC=AMAB.

    Suy ra BC = MN.ABAM=5.93= 15 (cm).

    Vậy NC = 8 cm, MN = 5 cm, BC = 15 cm.

    Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất

    Bài tập cuối chương 6 trang 30

    Bài 2: Đường trung bình của tam giác

    Bài 3: Tính chất đường phân giác của tam giác

    Bài tập cuối chương 7 trang 48

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 678 30/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: