Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 8 Bài 2 (Chân trời sáng tạo): Đường trung bình của tam giác

    Với giải sách bài tập Toán 8 Bài 2: Đường trung bình của tam giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 2.

    1 640 30/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 2: Đường trung bình của tam giác

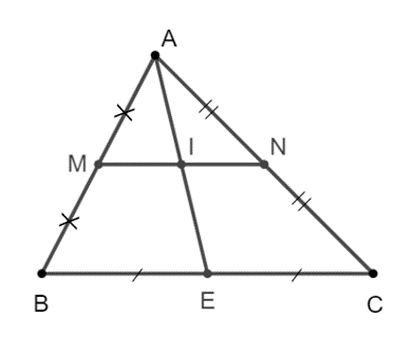
    Bài 1 trang 45 SBT Toán 8 Tập 2: Cho tam giác nhọn ABC có M, N lần lượt là trung điểm của AB, AC.

    Lời giải:

    a) Chứng minh tứ giác BMNC là hình thang.

    b) Gọi E là trung điểm của BC và I là giao điểm của AE với MN. Chứng minh I là trung điểm của MN.

    Lời giải

    Cho tam giác nhọn ABC có M, N lần lượt là trung điểm của AB, AC

    a) Xét ∆ABC, ta có MA = MB và NA = NC, nên MN là đường trung bình của ∆ABC.

    Suy ra MN // BC.

    Tứ giác BMNC có MN // BC nên BMNC là hình thang.

    b) Xét ∆ABE, ta có MA = MB và MI // BE (vì I ∈ MN, E ∈ BC) nên IA = IE.

    Do đó MI là đường trung bình của ∆ABE, suy ra MI = BE2.

    Tương tự, ta có IN = BE2.

    Mặt khác BE = EC, suy ra MI = IN.

    Vậy I là trung điểm của MN.

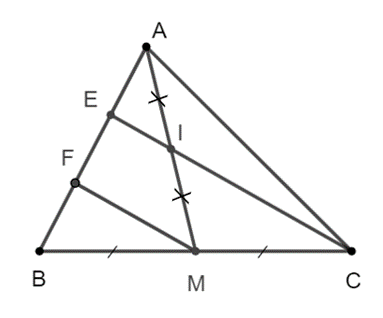
    Bài 2 trang 45 SBT Toán 8 Tập 2: Cho tam giác nhọn ABC, kẻ trung tuyển AM (M ∈ BC). Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh:

    a) EF = FB;

    b) AE = 13AB;

    c) CE = 4EI.

    Lời giải:

    Cho tam giác nhọn ABC, kẻ trung tuyển AM (M ∈ BC). Gọi I là trung điểm của AM

    a) Xét ∆BCE, ta có MB = MC và MF // CE nên EF = FB.

    b) Xét ∆AMF, ta có IA = IM và EI // MF (vì I ∈ CE) nên EA = EF.

    Suy ra EA = EF = FB mà EA + EF + FB = AB.

    Vậy AE = 13AB.

    c) Xét ∆BCE, ta có MB = MC và EF = FB, nên MF là đường trung bình của ∆BCE.

    Suy ra CE = 2MF (1)

    Tương tự, có EI là là đường trung bình của ∆AMF, suy ra MF = 2EI (2)

    Từ (1) và (2) suy ra CE = 4EI.

    Bài 3 trang 45 SBT Toán 8 Tập 2: Cho tam giác ABC, hai đường trung tuyến EM và CN cắt nhau tại G (M ∈ AC, N ∈ AB). Gọi D, E lần lượt là trung điểm của GB, GC. Chứng minh:

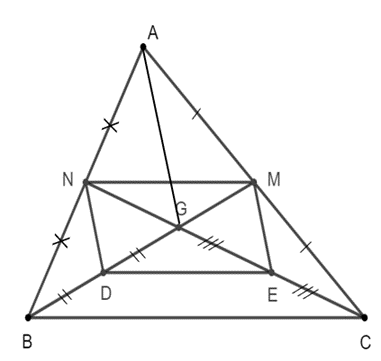
    a) MN // DE;

    b) ND // ME.

    Lời giải:

    Cho tam giác ABC, hai đường trung tuyến EM và CN cắt nhau tại G (M thuộc AC, N thuộc AB)

    a) Xét ∆ABC, ta có MA = MC và NA = NB nên MN là đường trung bình của ∆ABC.

    Suy ra MN // BC (1)

    Xét ∆BCG, ta có BD = DG và CE = EG nên DE là đường trung bình của ∆BCG.

    Suy ra DE // BC (2)

    Từ (1) và (2) suy ra MN // DE.

    b) Xét ∆ABG có NA = NB và DG = DB nên ND là đường trung bình của ∆ABG.

    Suy ra ND // AG (3)

    Xét ∆ACG có MA = MC và EG = EC nên ME là đường trung bình của ∆ACG.

    Suy ra ME // AG (4)

    Từ (3) và (4) suy ra ND // ME.

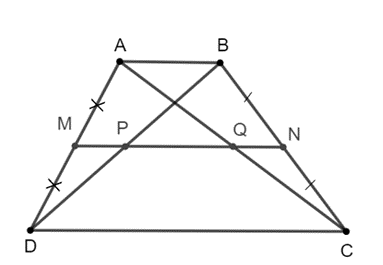
    Bài 4 trang 45 SBT Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, BC, BD, AC. Chứng minh bốn điểm M, N, P, Q thẳng hàng.

    Lời giải:

    Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, BC

    • Xét ∆ABD, ta có MA = MD và PB = PD nên MP là đường trung bình của ∆ABD.

    Suy ra MP //AB mà AB // CD nên MP // CD.

    • Xét ∆ADC, ta có MA = MD và QA = QC nên MQ là đường trung bình của ∆ADC.

    Suy ra MQ // CD.

    • Xét ∆BCD, ta có PB = PD và NB = NC nên BN là đường trung bình của ∆BCD.

    Suy ra PN // CD.

    Qua điểm M ∉ CD có MP // CD và MQ // CD, suy ra M, P, Q thẳng hàng. (1)

    Qua điểm P ∉ CD có MP // CD và PN // CD, suy ra M, P, N thẳng hàng. (2)

    Từ (1) và (2) suy ra bốn điểm M, N, P, Q thẳng hàng.

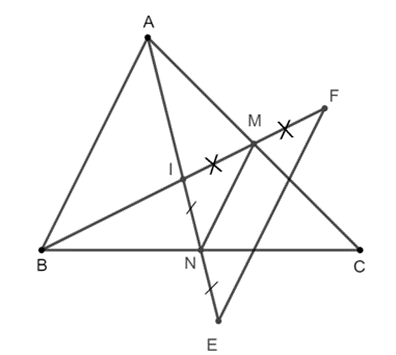
    Bài 5 trang 45 SBT Toán 8 Tập 2: Cho tam giác ABC có M, N lần lượt là trung điểm của AC, BC.

    a) Chứng minh tứ giác AMNB là hình thang.

    b) Gọi I là giao điểm của AN và BM.Trên tia đối của tia NA lấy điểm E sao cho NE = NI. Trên tia đối của tia MB lấy điểm F sao cho ME = MI. Chứng minh EF // AB.

    Lời giải:

    Cho tam giác ABC có M, N lần lượt là trung điểm của AC, BC

    a) Xét ∆ABC, ta có MA = MC và NB = NC nên MN là đường trung bình của ∆ABC.

    Suy ra MN // AB (1)

    Tứ giác AMNB có MN // AB nên AMNB là hình thang.

    b) Xét ∆IEF, ta có NE = NI và MF = MI nên MN là đường trung bình của ∆IEF.

    Suy ra MN // EF (2)

    Từ (1) và (2) suy ra EF // AB.

    Bài 6 trang 45 SBT Toán 8 Tập 2: Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // QO (M ∈ OP), IN // PO (N ∈ QO). Chứng minh:

    a) Tam giác IMN cân tại I;

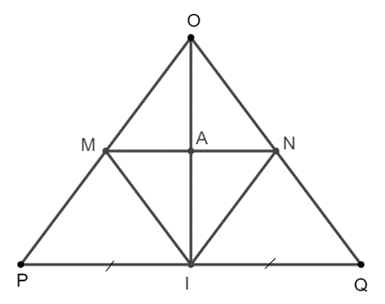
    b) OI là đường trưng trực của MN.

    Lời giải:

    Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // QO (M thuộc OP)

    a) Xét ∆OPQ, ta có IP = IQ và IM // QO nên MO = MP.

    Xét ∆OPQ, ta có IP = IQ và MO = MP nên IM là đường trung bình của ∆OPQ.

    Suy ra IM = 12QO.

    Tương tự, IN là đường trung bình của ∆OPQ, suy ra IN = 12PO.

    Mà ∆OPQ cân tại O nên QO = PO. Suy ra IM = IN.

    Tam giác IMN có IM = IN suy ra tam giác IMN cân tại I.

    b) Gọi A là giao điểm của IO và MN.

    ∆OPQ cân tại O có OI là đường trung tuyến, suy ra OI cũng là đường cao của ∆OPQ.

    Suy ra OI ⊥ PQ (1)

    Xét ∆OPQ, ta có MO = MP và NO = NQ nên MN là đường trung bình của ∆OPQ.

    Suy ra MN // PQ (2)

    Từ (1) và (2) suy ra MN ⊥ OI tại A hay MN ⊥ IA.

    Mà ∆IMN cân tại I có IA là đường cao nên IA cũng là đường trung trực của MN.

    Do đó, OI là đường trung trực của MN.

    Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất

    Bài tập cuối chương 6 trang 30

    Bài 1: Định lí Thalès trong tam giác

    Bài 3: Tính chất đường phân giác của tam giác

    Bài tập cuối chương 7 trang 48

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 640 30/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: