Nội dung bài viết

    Xem thêm

    Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi

    Lời giải Bài 8 trang 57 SBT Toán 8 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

    1 275 10/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 2: Tứ giác

    Bài 8 trang 57 SBT Toán 8 Tập 1: Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi của tứ giác đó.

    Lời giải:

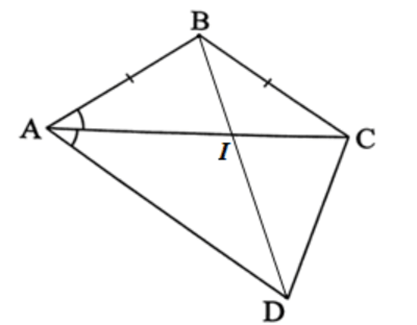
    Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi

    Vẽ tứ giác ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.

    Theo bất đẳng thức tam giác, ta có:

    IA + IB > AB (trong tam giác IAB)

    IB + IC > BC (trong tam giác IBC)

    IC + ID > CD (trong tam giác ICD)

    IA + ID > AD (trong tam giác IAD)

    Suy ra2(IA + IB + IC + ID) > AB + BC + CD + DA

    Hay 2(AC + BD) > AB + BC + CD + DA

    Vậy AC+BD>AB+BC+CD+DA2 hay tổng độ dài hai đường chéo của một tứ giác lớn hơn nửa chu vi của tứ giác đó.

    Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 56 SBT Toán 8 Tập 1: Tìm tứ giác lồi trong các hình sau:...

    Bài 2 trang 57 SBT Toán 8 Tập 1: Tìm số đo x trong các tứ giác sau:...

    Bài 3 trang 57 SBT Toán 8 Tập 1: Cho tứ giác ABCD như Hình 12....

    Bài 4 trang 57 SBT Toán 8 Tập 1: Bạn Hùng muốn làm một cái diều có dạng hình tứ giác KITE...

    Bài 5 trang 57 SBT Toán 8 Tập 1: Cho tứ giác ABCD có...

    Bài 6 trang 57 SBT Toán 8 Tập 1: Cho tứ giác ABCD có AB = AD, CB = CD, ...

    Bài 7 trang 57 SBT Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I...

    Bài 8 trang 57 SBT Toán 8 Tập 1: Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi của tứ giác đó....

    Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1: Định lí Pythagore

    Bài 3: Hình thang – Hình thang cân

    Bài 4: Hình bình hành – Hình thoi

    Bài 5: Hình chữ nhật – Hình vuông

    Bài tập cuối chương 3 trang 72

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 275 10/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: