Sách bài tập Toán 7 (Kết nối tri thức) Ôn tập chương 7

Giải sách bài tập Toán lớp 7 Ôn tập chương 7  - Kết nối tri thức

Giải SBT Toán 7 trang 35 Tập 2

Câu 1 trang 35 SBT Toán 7 tập 2: Biểu thức nào sau đây không là đa thức một biến?

A. $\sqrt{3}$ ;

B. – x;

C. x + $\frac{-1}{x}$ ;

D.  $\frac{x}{\sqrt{2}}$ − 1.

Lời giải:

Đáp án đúng là: C.

x +  $\frac{-1}{x}$ không phải đa thức một biến vì $\frac{-1}{x}$  không phải là đơn thức theo biến x.

Câu 2 trang 35 SBT Toán 7 tập 2: Cho đa thức G(x) = 4x³ + 2x² − 5x. Hệ số cao nhất và hệ số tự do của G(x) lần lượt là:

A. 4 và 0;

B. 0 và 4;

C. 4 và – 5;

D. – 5 và 4.

Lời giải:

Đáp án đúng là : A.

Vì đa thức G(x) = 4x³ + 2x² − 5x có hạng tử có bậc cao nhất là 4x³, bậc 3, nên G(x) có hệ số cao nhất là 4 và hệ số tự do là 0.

Câu 3 trang 35 SBT Toán 7 tập 2: Cho hai đa thức f(x) và g(x) khác đa thức không sao cho tổng f(x) + g(x) khác đa thức không. Khi nào thì bậc của f(x) + g(x) chắc chắn bằng bậc của f(x)?

A. f(x) và g(x) có cùng bậc;

B. f(x) có bậc lớn hơn bậc của g(x);

C. g(x) có bậc lớn hơn bậc của f(x);

D. Không bao giờ.

Lời giải:

Đáp án đúng là : B.

Trong mọi trường hợp khi f(x) có bậc lớn hơn bậc của g(x) thì bậc của f(x) + g(x) chắc chắn bằng bậc của f(x).

Câu 4 trang 35 SBT Toán 7 tập 2: Cho đa thức P(x) = x² + 5x − 6. Khi đó:

A. P(x) chỉ có một nghiệm là x = 1;

B. P(x) không có nghiệm;

C. P(x) chỉ có một nghiệm là x = −6;

D. x = 1 và x =  −6 là hai nghiệm của P(x).

Lời giải:

Đáp án đúng là: D.

Thay x = 1 và x = −6 vào P(x) ta có:

P(1) = 1² + 5.1 −6 = 1 + 5 −6 = 0

P(−6) = (−6)² + 5.(– 6) − 6 = 36 − 30 − 6 = 0

Do đó x = 1 và x =  −6 là hai nghiệm của P(x).

Câu 5 trang 35 SBT Toán 7 tập 2: Phép chia đa thức $2x^5-3x^4+x^3-6x^2$  cho đa thức $5x^{7-2n}$ ( n $\in$ ℕ và 0 ≤ n ≤ 3 ) là phép chia hết nếu

A. n = 0;

B. n = 1;

C. n = 2;

D. n = 3.

Lời giải:

Đáp án đúng là : D.

Đa thức đã cho chia hết cho $5x^{7-2n}$ nếu từng hạng tử của nó chia hết cho $5x^{7-2n}$ , nói riêng thì bậc của $5x^{7-2n}$ nhỏ hơn hoặc bằng bậc nhỏ nhất của đa thức.

Khi đó 7 − 2n ≤ 2 ⇔ n ≥ $\frac{5}{2}$ . Chỉ có n = 3 thỏa yêu cầu đề bài.

Bài 7.34 trang 35 SBT Toán 7 Tập 2: Thu gọn và sắp xếp các đa thức sau theo lũy thừa giảm của biến. Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đó.

a) x⁵ + 7x² − x − 2x⁵ + 3 − 5x²;

b) 4x³ − 5x² + x − 4x³ + 3x² − 2x + 6.

Lời giải:

a) x⁵ + 7x² − x − 2x⁵ + 3 − 5x²

= (x⁵ − 2x⁵) + (7x² − 5x²) − x + 3

= −x⁵ + 2x² − x + 3

Vì đa thức trên có hạng tử có bậc cao nhất là −x⁵ nên đa thức có bậc 5, hệ số cao nhất là −1 và hệ số tự do là 3.

b) 4x³ − 5x² + x − 4x³ + 3x² − 2x + 6

= (4x³ − 4x³) + (−5x² + 3x²) + (x − 2x) + 6

= −2x² − x + 6

Vì đa thức trên có hạng tử có bậc cao nhất là −2x² nên đa thức có bậc 2, hệ số cao nhất là −2, hệ số tự do là 6.

Giải SBT Toán 7 trang 36 Tập 2

Bài 7.35 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức f(x) = 4x⁴ − 5x³ + 3x + 2 và g(x) = −4x⁴ + 5x³ + 7. Trong các số −4; −3; 0 và 1, số nào là nghiệm của đa thức f(x) + g(x)?

Lời giải:

Ta có: f(x) + g(x)

= (4x⁴ − 5x³ + 3x + 2) + (−4x⁴ + 5x³ + 7)

= 4x⁴ − 5x³ + 3x + 2 −4x⁴ + 5x³ + 7

= (4x⁴ −4x⁴) + (−5x³ + 5x³) + 3x + (2 + 7)

= 3x + 9.

Để tìm nghiệm của đa thức f(x) + g(x) thì đa thức phải bằng 0.

Suy ra 3x + 9 = 0

x = (−9) : 3 = −3

Vậy nghiệm của đa thức f(x) + g(x) là x = −3

Bài 7.36 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức f(x) = −x⁵ + 3x² + 4x + 8  và g(x) = −x⁵ − 3x² + 4x + 2. Chứng minh rằng đa thức f(x) – g(x) không có nghiệm.

Lời giải:

Ta có f(x) – g(x)

= (−x⁵ + 3x² + 4x + 8) – (−x⁵ − 3x² + 4x + 2)

= −x⁵ + 3x² + 4x + 8 + x⁵ + 3x² – 4x – 2

= (−x⁵ + x⁵) + (3x² + 3x²) + (4x – 4x) + (8 – 2)

= 6x² + 6

Vì f(x) – g(x) = 6x² + 6 ≥ 6 với mọi x nên f(x) – g(x) không có nghiệm.

Bài 7.37 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức sau:

P(x) = 3x⁵ – 2x⁴ + 7x² + 3x – 10

Q(x) = –3x⁵ – x³ – 7x² + 2x + 10

a) Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức

S(x) = P(x) + Q(x) và D(x) = P(x) – Q(x)

b) Trong tập hợp {–1; 0; 1}, tìm những số là nghiệm của một trong hai đa thức S(x) và D(x).

Lời giải:

a) S(x) = P(x) + Q(x)

= (3x⁵ – 2x⁴ + 7x² + 3x – 10) + (–3x⁵ – x³ – 7x² + 2x + 10)

= 3x⁵ – 2x⁴ + 7x² + 3x – 10 – 3x⁵ – x³ – 7x² + 2x + 10

= (3x⁵ – 3x⁵) – 2x⁴ – x³ + (7x² – 7x²) + (3x + 2x) + (–10 + 10)

= –2x⁴ – x³ + 5x

S(x) = –2x⁴ – x³ + 5x là đa thức bậc 4 với hệ số cao nhất là –2 và hệ số tự do là 0.

D(x) = P(x) – Q(x)

= (3x⁵ – 2x⁴ + 7x² + 3x – 10) − (–3x⁵ – x³ – 7x² + 2x + 10)

= 3x⁵ – 2x⁴ + 7x² + 3x – 10 + 3x⁵ + x³ + 7x² – 2x – 10

= (3x⁵ + 3x⁵ ) – 2x⁴ + x³ + (7x² + 7x²)+ (3x – 2x) + (–10 – 10)

= 6x⁵ – 2x⁴ + x³  + 14x² + x – 20

D(x) = 6x⁵ – 2x⁴ + x³  + 14x² + x – 20 là đa thức bậc 5 với hệ số cao nhất là 6 và hệ số tự do là – 20

b) Xét đa thức S(x):

+) Thay x = – 1 vào đa thức S(x) ta được:

S(0) = –2.(– 1)⁴ – (– 1)³ + 5.(– 1) = – 6 ≠ 0

Do đó x = – 1 không là nghiệm của đa thức S(x).

+) Thay x = 0 vào đa thức S(x) ta được:

S(0) = –2.0⁴ – 0³ + 5.0 = 0

Do đó x = 0 là nghiệm của đa thức S(x).

+) Thay x = 1 vào đa thức S(x) ta được:

S(0) = –2.1⁴ – 1³ + 5.1 = 2 ≠ 0

Do đó x = 1 không là nghiệm của đa thức S(x).

Xét đa thức D(x):

+) Thay x = – 1 vào đa thức D(x) ta được:

D(1) = 6.(– 1)⁵ – 2.(– 1)⁴ + (– 1)³  + 14.(– 1)² + (– 1) – 20 = – 6 – 2 – 1 + 14 – 1 – 20 = – 16 ≠ 0.

Do đó x = – 1 không là nghiệm của đa thức D(x).

+) Thay x = 0 vào đa thức D(x) ta được:

D(1) = 6.0⁵ – 2.0⁴ + 0³  + 14.0² + 0 – 20 = – 20 ≠ 0

Do đó x = 0 không là nghiệm của đa thức D(x).

+) Thay x = 1 vào đa thức D(x) ta được:

D(1) = 6.1⁵ – 2.1⁴ + 1³  + 14.1² + 1 – 20 = 6 – 2 + 1 + 14 + 1 – 20 = 0

Do đó x = 1 là nghiệm của đa thức D(x).

Vậy x = 0 là nghiệm của đa thức S(x) và x = 1 là nghiệm của đa thức D(x).

Bài 7.38 trang 36 SBT Toán 7 Tập 2: Biết rằng đa thức f(x) = x⁴ + px³ – 2x² + 1  có hai nghiệm (khác 0) là hai số đối nhau. Chứng minh rằng p = 0.

Lời giải:

Gọi hai nghiệm đối nhau của f(x) là a và – a (a ≠ 0). Khi đó ta có:

f(a) = a⁴ + pa³ – 2a² + 1 = 0 = f(– a) = (– a)⁴ + p(–a)³ – 2(–a)² + 1

Suy ra:

a⁴ + pa³ – 2a² + 1 = a⁴ – pa³ – 2a² + 1

Thu gọn ta được pa³ = –pa³, suy ra 2pa³ = 0 . Do a ≠ 0 nên từ đẳng thức này suy ra p = 0.

Bài 7.39 trang 36 SBT Toán 7 Tập 2: Thực hiện các phép tính sau:

a) (5x³ – 2x² + 4x – 4)(3x² + x – 1);

b) (9x⁵ – 6x³ + 18x² – 35x – 42) : ( 3x³ + 5x + 6);

c) $\left[\left(6x^3-5x^2-8x+5\right)-(4x^2-6x+2)\right]$ : (2x – 3).

Lời giải:

a) (5x³ – 2x² + 4x – 4)(3x² + x – 1)

= 3x²(5x³ – 2x² + 4x – 4) + x(5x³ – 2x² + 4x – 4) – 1(5x³ – 2x² + 4x – 4)

= 15x⁵ – 6x⁴ + 12x³ – 12x² + 5x⁴ – 2x³ + 4x² – 4x – 5x³ + 2x² – 4x + 4

= 15x⁵ + (–6x⁴ + 5x⁴) + (12x³ – 2x³ – 5x³) + (–12x² + 4x² + 2x²)+ (–4x– 4x) + 4

= 15x⁵ – x⁴ + 5x³ – 6x² – 8x + 4

b) (9x⁵ – 6x³ + 18x² – 35x – 42) : ( 3x² + 5x + 6)

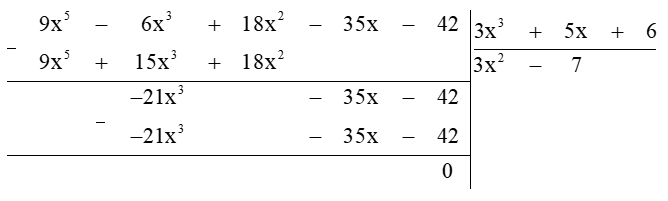
Vậy phép chia (9x⁵ – 6x³ + 18x² – 35x – 42) : ( 3x² + 5x + 6) có thương là 3x² − 7 và dư 0.

c) $\left[\left(6x^3-5x^2-8x+5\right)-(4x^2-6x+2)\right]$ : (2x – 3)

Tính (6x³ − 5x² − 8x + 5) − (4x² − 6x + 2)

= 6x³ − 5x² − 8x + 5 − 4x² + 6x − 2

= 6x³  + (−5x² − 4x²) + (−8x + 6x) + (5 − 2)

= 6x³  − 9x² − 2x  + 3

Ta thực hiện tiếp phép chia (6x³  − 9x² − 2x  + 3) : (2x – 3)

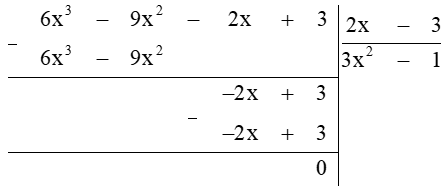
Vậy phép chia $\left[\left(6x^3-5x^2-8x+5\right)-(4x^2-6x+2)\right]$ : (2x – 3) có thương là 3x² − 1 và số dư là 0

Bài 7.40 trang 36 SBT Toán 7 Tập 2: Rút gọn các biểu thức sau:

a) A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3)

b) B = (x − 1)(x + 1)( x² + 1)(x⁴ +1) − x⁸

Lời giải:

a) A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3)

Ta có:

 (x − 1)(x + 2)(x − 3)

= [x(x + 2) − 1(x + 2)](x − 3)

= (x² + 2x − x − 2)(x − 3)

= (x² + x − 2)(x − 3)

= x(x² + x − 2) − 3(x² + x − 2)

= x³ + x² − 2x − 3x² − 3x + 6

= x³ + (x² − 3x²) +  (−2x − 3x) + 6

= x³ − 2x² − 5x + 6 (1)

(x + 1)(x − 2)(x + 3)

= [x(x − 2) + 1(x − 2)](x + 3)

= (x² − 2x + x − 2)(x + 3)

= (x² − x − 2)(x + 3)

= x(x² − x − 2) + 3(x² − x − 2)

= x³ − x² − 2x + 3x² − 3x − 6

= x³ + (−x² + 3x²) +  (−2x − 3x) − 6

= x³ + 2x² − 5x − 6 (2)

Khi đó: A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3) = (1) − (2)

= (x³ − 2x² − 5x + 6) − (x³ + 2x² − 5x − 6)

= x³ − 2x² − 5x + 6 − x³ − 2x² + 5x + 6

= (x³ − x³) + (−2x² − 2x²) + (−5x + 5x) + (6 + 6)

= −4x² + 12.

b) B = (x − 1)(x + 1)( x² + 1)(x⁴ +1) − x⁸

Với M là một biểu thức tùy ý, ta có:

(M − 1)(M + 1) = M² − M + M − 1 hay (M − 1)(M + 1) = M² − 1  (1)

Từ đó, ta có:

(x − 1)(x + 1)  (áp dụng (1) với M = x)

(x² − 1)(x² + 1) = (x²)² − 1 = x⁴ − 1  (áp dụng (1) với M = x²)

(x⁴ − 1)(x⁴ + 1) = (x⁴)² − 1 = x⁸ − 1 (áp dụng (1) với M = x⁴).

Sử dụng các kết quả trên, ta được:

(x − 1)(x + 1)(x² + 1)(x⁴ + 1)

= $\left[(x-1)(x+1)\right]$ (x² +1)(x⁴ + 1)

= (x² − 1)(x² + 1)(x⁴  + 1)

= $\left[(x^2-1)(x^2+1)\right]$ (x⁴ + 1)

= (x⁴ − 1)(x⁴ + 1)

= x⁸ − 1.

Vậy B = (x − 1)(x + 1)( x² + 1)(x⁴ +1) − x⁸ = x⁸ – 1 − x⁸ = −1.

Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Bài 27: Phép nhân đa thức một biến

Bài 28: Phép chia đa thức một biến

Bài 29: Làm quen với biến cố

Bài 30: Làm quen với xác suất của biến cố

Ôn tập chương 8