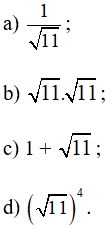Sách bài tập Toán 7 Bài 7 (Kết nối tri thức): Tập hợp các số thực

Giải sách bài tập Toán lớp 7 Bài 7: Tập hợp các số thực - Kết nối tri thức

Giải SBT Toán 7 trang 31 Tập 1

Bài 2.22 trang 31 SBT Toán 7 Tập 1: Kí hiệu $\mathrm{N};\mathrm{Z};\mathrm{Q};\mathrm{I};\mathrm{R}$ theo thứ tự là tập hợp các số tự nhiên, tập hợp các số nguyên, tập hợp các số hữu tỉ, tập hợp các số vô tỉ và tập hợp các số thực. Khẳng định nào sau đấy sai?

A. Nếu $x\in N$ thì $x\in Z$;

B. Nếu $x\in R$ và $x\notin Q$ thì $x\in I$;

C. $1\in R$;

D. Nếu $1\notin I$ thì x viết được thành số thập phân hữu hạn.

Lời giải:

A. Khẳng  định A đúng vì tất cả các số tự nhiên đều là số nguyên;

B. Khẳng định B đúng vì tập số thực gồm có số hữu tỉ và số vô tỉ nên nếu x không là số hữu tỉ thì x là số vô tỉ.

C. Khẳng định C đúng vì 1 là số thực.

D. Khẳng định D sai vì nếu x không là số vô tỉ thì x là số hữu tỉ mà số hữu tỉ gồm số thập phân hữu hạn và số thập phân vô hạn tuần hoàn nên khẳng định D sai.

Vậy khẳng định sai là D.

Bài 2.23 trang 31 SBT Toán 7 Tập 1: Xét tính đúng, sai của các khẳng định sau:

a) Nếu x là số hữu tỉ thì x là số thực;

b) 2 không phải là số hữu tỉ;

c) Nếu x là số nguyên thì $\sqrt{x}$ là số thực;

d) Nếu x là số tự nhiên thì $\sqrt{x}$ là số vô tỉ.

Lời giải:

a) Nếu x là số hữu tỉ thì x là số thực. Khẳng định này đúng vì mọi số hữu tỉ đều là số thực.

b) 2 không phải là số hữu tỉ. Khẳng định này sai vì 2 là số nguyên nên 2 là số hữu tỉ.

c) Nếu x là số nguyên thì $\sqrt{x}$ là số thực. Khẳng định này sai vì nếu x < 0 thì không tồn tại $\sqrt{x}$.

d) Nếu x là số tự nhiên thì $\sqrt{x}$ là số vô tỉ. Khẳng định này sai vì nếu x = 25 thì $\sqrt{x}=\sqrt{25}$ = 5 là số hữu tỉ.

Bài 2.24 trang 31 SBT Toán 7 Tập 1: Tìm số đối của các số thực sau: -2,1; -0,(1); $\frac{2}{\mathrm{\pi }}$; 3 – $\sqrt{2}$.

Lời giải:

Số đối của số -2,1 là 2,1 vì (-2,1) + 2,1 = 0;

Số đối của số  -0,(1) là 0,(1) vì -0,(1) + 0,(1) = 0;

Số đối của $\frac{2}{\pi }$ là $-\frac{2}{\pi }$ vì $\frac{2}{\pi }$ + $\left(\frac{-2}{\mathrm{\pi }}\right)$ = 0

Số đối của  3 – $\sqrt{2}$ là -3 + $\sqrt{2}$ vì 3 – $\sqrt{2}$ + (-3) + $\sqrt{2}$ = 0.

Giải SBT Toán 7 trang 32 Tập 1

Bài 2.25 trang 32 SBT Toán 7 Tập 1: So sánh a = 1,(41) và $\sqrt{2}$.

Lời giải:

a = 1,(41) = 1,414141….

$\sqrt{2}=1,\mathrm{414213...}$

Kể từ trái sang phải, chữ số cùng hàng đầu tiên khác nhau nằm ở hàng phần chục nghìn. Mà 1 < 2 nên 1,414141… < 1,414213…

Do đó, a = 1,(41) < $\sqrt{2}$.

Bài 2.26 trang 32 SBT Toán 7 Tập 1: Viết các số thực sau theo thứ tự từ bé đến lớn:

$\sqrt{5};-1,7\left(5\right);\pi ;-2;\frac{22}{7};0$.

Lời giải:

Ta chia các số thực đã cho thành ba nhóm.

Nhóm số thực không âm, không dương: 0

Nhóm số thực âm: -1,7(5); -2;

Nhóm số thực dương: $\sqrt{5};\pi ;\frac{22}{7}$

Ta đi so sánh nhóm số thực âm.

Thay vì so sánh  -1,7(5) và -2 ta đi so sánh hai số đối của chúng là 1,7(5) và 2.

Nhận thấy 1,7(5) có phần nguyên là 1 < 2 nên 1,7(5) < 2. Do đó, -1,7(5) > -2.

Ta đi so sánh nhóm số thực dương.

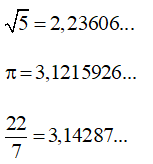
Ta thấy 2 < 3 nên số nào có phần nguyên là 2 sẽ bé hơn số có phần nguyên là 3. Do đó, $\sqrt{5}$ nhỏ nhất trong ba số.

Ta đi so sánh $\mathrm{\pi }$ và $\frac{22}{7}$.

Ta có: 

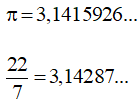
Nhận thấy chữ số cùng hàng đầu tiên khác nhau là chữ số hàng nghìn. Vì 1 < 2 nên 3,1415926… < 3,14287…hay $\pi <\frac{22}{7}$ 

Sắp xếp các số đã cho theo thứ tự từ bé đến lớn như sau:

-2 < -1,7(5) < 0 < $\sqrt{5}<\pi <\frac{22}{7}$.

Bài 2.27 trang 32 SBT Toán 7 Tập 1: Tìm các số thực x có giá trị tuyệt đối bằng 1,6(7). Điểm biểu diễn các số thực tìm được nằm trong hay nằm ngoài khoảng giữa hai điểm -2 và 2,(1) trên trục số?

Lời giải:

Ta có:

|x| = 1,6(7) nên x = 1,6(7) hoặc x = -1,6(7)

Ta so sánh 1,6(7) với -2 và 2,(1)

Vì 1,6(7) là số thực dương còn -2 là số thực âm nên 1,6(7) > -2.

Lại có phần nguyên của 1,6(7) là 1 và phần nguyên của 2,(1) là 2 nên 1,6(7) < 2.

Vậy 1,6(7) nàm trong khoảng -2 và 2,(1).

Ta so sánh -1,6(7) với -2 và 2,(1)

Ta có: -1,6(7) là số thực âm và 2,(1) là số thực dương nên -1,6(7) < 2,(1).

Số đối của -1,6(7) là 1,6(7) và số đối của -2 là 2. Vì 1,6(7) có phần nguyên là 1 < 2 nên 1,6(7) < 2. Do đó, -1,6(7) > -2.

Vậy -1,6(7) nằm trong khoảng -2 và 2,(1).

Bài 2.28 trang 32 SBT Toán 7 Tập 1: Xác định dấu và giá trị tuyệt đối của các số thực sau:

a) -1,3(51);

b) $1-\sqrt{2}$;

c) $\left(3-\sqrt{2}\right)\left(2-\sqrt{5}\right)$

Lời giải:

a) -1,3(51) mang dấu âm và |-1,3(51)| = 1,3(51).

b) 

Vì 1 < 2 nên $\sqrt{1}<\sqrt{2}$ hay 1 < $\sqrt{2}$

Do đó 1 – $\sqrt{2}$ < 0 nên 1 – $\sqrt{2}$ mang dấu âm.

|1 – $\sqrt{2}$| = -(1 – $\sqrt{2}$) = $\sqrt{2}$ - 1.

c) 

Vì 9 > 2 nên $\sqrt{9}>\sqrt{2}$ hay 3 > $\sqrt{2}$. Do đó, $3-\sqrt{2}$ > 0.

Lại có 4 < 5 nên $\sqrt{4}<\sqrt{5}$ hay $2<\sqrt{5}$. Do đó, 2 – $\sqrt{5}$ < 0.

Vì $3-\sqrt{2}$ > 0 vad 2 – $\sqrt{5}$ < 0 nên $\left(3-\sqrt{2}\right)\left(2-\sqrt{5}\right)$ < 0

Ta có: 

Bài 2.29 trang 32 SBT Toán 7 Tập 1: Không sử dụng máy tính cầm tay, ước lượng giá trị thập phân của số $\sqrt{3}$ với độ chính xác 0,05.

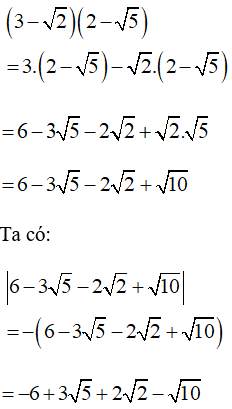
Lời giải:

Muốn ước lượng giá trị thập phân của $\sqrt{3}$với độ chính xác 0,05 ta phải làm tròn số đó đến hàng phần mười.

Trong ví dụ 3 (trang 32) ta thấy 1,7 < $\sqrt{3}$ < 1,8. Cần xét xem $\sqrt{3}$ gần với 1,7 hơn hay 1,8 hơn. Muốn vậy ta xét số $\frac{1,7+1,8}{2}=1,75$ điểm biểu diễn số 1,75 cách đều 1,7 và 1,8.

Ta có (1,75)² = 3,0625, do đó 3 < (1,75)² < 1,75. Vì vậy $\sqrt{3}<\sqrt{{\left(1,75\right)}^2}$  

Suy ra, $\sqrt{3}<1,75$. Từ đó, 1,7 < $\sqrt{3}$ < 1,75. Vì vậy $\sqrt{3}$ gần 1,7 hơn so với 1,8.

Vậy làm tròn giá trị thập phân của $\sqrt{3}$ đến hàng phần mười (độ chính xác 0,05) ta được $\sqrt{3}\approx 1,7$.

Bài 2.30 trang 32 SBT Toán 7 Tập 1: Tính $\left|6-\sqrt{35}\right|+5+\sqrt{35}$

Lời giải:

Ta có

Bài 2.31 trang 32 SBT Toán 7 Tập 1: Biết $\sqrt{11}$ là số vô tỉ. Trong các phép tính sau, những phép tính nào có kết quả là số hữu tỉ?

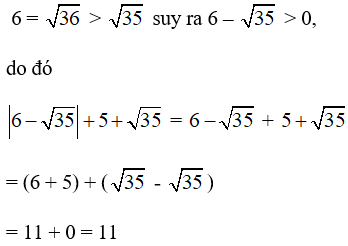
Lời giải:

a) $\frac{1}{\sqrt{11}}$ phép tính này không cho ta kết quả là số hữu tỉ;            

b) $\sqrt{11}.\sqrt{11}=\sqrt{11.11}$$=\sqrt{{11}^2}=11$ phép tính này cho ta kết quả là số hữu tỉ;

c) 1 + $\sqrt{11}$ phép tính này không cho ta kết quả là số hữu tỉ;                

d) ${\left(\sqrt{11}\right)}^4=\sqrt{11}.\sqrt{11}.\sqrt{11}.\sqrt{11}$$=\left(\sqrt{11}.\sqrt{11}\right).\left(\sqrt{11}.\sqrt{11}\right)$$=11.11=121$ phép tính này cho ta kết quả là số hữu tỉ.

Bài 2.32 trang 32 SBT Toán 7 Tập 1: Tính giá trị của các biểu thức sau:

a) $\sqrt{0,25}-\sqrt{0,49}$;

b) 0,2.$\sqrt{100}-\sqrt{0,25}$.

Lời giải:

a) $\sqrt{0,25}-\sqrt{0,49}=\sqrt{0,5^2}-\sqrt{0,7^2}$ = 0,5 – 0,7 = 0,2;

b) 0,2.$\sqrt{100}-\sqrt{0,25}$ = 0,2.10 – 0,5 = 2 – 0,5 = 1,5.

Bài 2.33 trang 32 SBT Toán 7 Tập 1: So sánh a = 0,(12) và b = 0,1(21).

Lời giải:

Ta thấy 100a = 12(12) = 12 + a nên 99a = 12, suy ra a = $\frac{12}{99}$.

Tương tự, b = 0,1 + 0,0(21) = $\frac{1}{10}+\frac{1}{10}.0,\left(21\right)$

Đặt x = 0,(21) thì 100x = 21,(21) = 21 + x suy ra x = $\frac{21}{99}$ 

Và b = $\frac{1}{10}+\frac{1}{10}.\frac{21}{99}=\frac{1}{10}\left(1+\frac{21}{99}\right)$$=\frac{1}{10}.\frac{120}{99}=\frac{12}{99}$.

Vậy a = b

Bài 2.34 trang 32 SBT Toán 7 Tập 1: Tìm giá trị nhỏ nhất của biểu thức A = $2+3\sqrt{x^2+1}$.

Lời giải:

Ta có: x² $\ge$ 0 với mọi số thực x nên x² + 1 $\ge$1 với mọi số thực x.

Suy ra: $\sqrt{x^2+1}\ge \sqrt{1}$ nên $\sqrt{x^2+1}\ge 1$.

Vì $\sqrt{x^2+1}\ge 1$ nên $3.\sqrt{x^2+1}\ge 3.1$ hay $3.\sqrt{x^2+1}\ge 3$

Suy ra A = 2 + $3.\sqrt{x^2+1}\ge 2+3=5$

Vậy A_min = 5 khi x = 0.

Bài 2.35 trang 32 SBT Toán 7 Tập 1: Tìm giá trị nhỏ nhất của biểu thức B = |x – 1| + |x – 3|.

Lời giải:

Xét các điểm biểu diễn số thực x trên trục số. Biểu thức đã cho đúng bằng tổng các khoảng cách từ x tới hai điểm 1 và 3. Nếu x nằm ngoài đoạn giữa 1 và 3 thì tổng hai khoảng cách trên lớn hơn khoảng cách giữa 1 và 3. Nếu x nằm trong đoạn giữa 1 và 3 thì tổng hai khoảng cách nói trên đúng bằng khoảng cách giữa 1 và 3. Vì vậy, biểu thức B đã cho có giá trị nhỏ nhất là 2 (đạt được khi 1 $\le x\le$2).

Bài 2.36 trang 32 SBT Toán 7 Tập 1: Hãy giải thích tại sao |x + y| $\le$ |x| + |y| với mọi số thực x, y.

Lời giải:

Xét hai trường hợp:

Nếu x + y $\ge$0 thì |x + y| = x + y $\le$|x| + |y| (vì x $\le$|x| với mọi số thực x)

Nếu x + y < 0 thì |x + y| = -x – y $\le$ |-x| + |-y| = |x| + |y|.

Vậy với mọi x, y là số thực thì ta luôn có |x + y| $\le$ |x| + |y|.

Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Ôn tập chương 2

Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc

Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết

Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song

Bài 11: Định lí và chứng minh định lí

Xem thêm tài liệu Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 7. Tập hợp các số thực