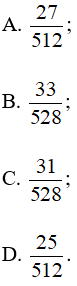Sách bài tập Toán 7 (Kết nối tri thức): Ôn tập chương 2

Giải sách bài tập Toán lớp 7 Ôn tập chương 2 - Kết nối tri thức

Giải SBT Toán 7 trang 33 Tập 1

Tìm câu trả lời đúng trong các đáp án đã cho.

A – Câu hỏi (trắc nghiệm)

Câu hỏi số 1 trang 33 SBT Toán 7 Tập 1: Số nào sau đây viết được dưới dạng số thập phân vô hạn tuần hoàn?

Lời giải:

Đáp án đúng là: C

Ta có:

$\frac{27}{512}$ là phân số tối giản và có mẫu số là 512. Ta có 512 = 2⁹ nên $\frac{27}{512}$ có thể viết được dưới dạng số thập phân hữu hạn.

$\frac{33}{528}=\frac{1}{16}$. Ta thấy $\frac{1}{16}$ có mẫu số là 16 mà 16 = 2⁴ nên $\frac{1}{16}$ có thể viết được dưới dạng số thập phân hữu hạn hay $\frac{33}{528}$ có thể viết dưới dạng số thập phân hữu hạn.

$\frac{31}{528}$ đây là phân số tối giản có mẫu số là 528. Ta có 528 = 2⁴.3.11 nên $\frac{31}{528}$ viết được dưới dạng số thập phân vô hạn tuần hoàn.

$\frac{25}{528}$ đây là phân số tối giản có mẫu số là 512 = 2⁹ nên có thể viết được dưới dạng số thập phân hữ hạn.

Câu hỏi số 2 trang 33 SBT Toán 7 Tập 1: Số 3,(5) viết được thành phân số nào sau đây?

A. $\frac{41}{11}$;

B. $\frac{32}{9}$;

C. $\frac{42}{11}$;

D. $\frac{31}{9}$.

Lời giải:

Đáp án đúng là B

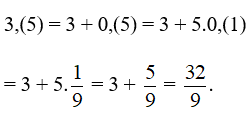
Câu hỏi số 3 trang 33 SBT Toán 7 Tập 1: Số nào dưới đây là bình phương của một số hữu tỉ?

A. 17;

B. 153;

C. 15,21;

D. 0,10100100010000…(viết liên tiếp sau dấu phẩy các lũy thừa của 10: 1010010001000…)

Lời giải:

Đáp án đúng là C

Ta đã biết, căn bậc hai số học của các số tự nhiên không chính phương đều là số vô tỉ nên 17 không phải là bình phương của một số hữu tỉ.

Mặt khác vì 153 = 17.9 nên nếu 153 là bình phương của số hữu tỉ x thì 17.9 = x², nên 17 = ${\left(\frac{x}{3}\right)}^2$ suy ra 17 là bình phương của số hữu tỉ $\frac{x}{3}$ (vô lí).

Do đó, A và B đều sai. Mặt khác, nếu 0,101001000… là bình phương của số hữu tỉ $\frac{p}{q}$ thì 0,101001000… = $\frac{p}{q}.\frac{p}{q}$. Suy ra 0,101001000.. là số thập phân vô hạn tuần oàn, điều này là vô lí. Do đó, D sai nên chỉ còn C đúng.

Ta sẽ thấy 15,21 = 3,9².

Câu hỏi số 4 trang 33 SBT Toán 7 Tập 1: Giá trị nhỏ nhất của biểu thức $\sqrt{x^2+16}-8$ là:

A. -4

B. 8

C. 0

D. -8

Lời giải:

Đáp án đúng là: A

Vì x² $\ge$0 nên x² +16 $\ge$0 + 16 = 16, do đó, $\sqrt{x^2+16}\ge \sqrt{16}=4$ 

nên $\sqrt{x^2+16}-8\ge 4-8=-4$.

Vậy giá trị nhỏ nhất của biểu thức là -4. Dấu “=” xảy ra khi x = 0.

Câu hỏi số 5 trang 33 SBT Toán 7 Tập 1: Giá trị lớn nhất của biểu thức $2-4\sqrt{x-5}$ là:

A. -2;

B. $2-4\sqrt{5}$;

C. 2;

D. $2+4\sqrt{5}$.

Lời giải:

Đáp án đúng là: C

Để căn xác định thì x $\ge$5

Với mọi x $\ge$5 thì $\sqrt{x-5}\ge 0$ nên $4.\sqrt{x-5}\ge 4.0=0$

Do đó, $-4.\sqrt{x-5}\le 0$ nên $2-4\sqrt{x-5}\le 2-0$ hay $2-4\sqrt{x-5}\le 2$

Vậy giá trị lớn nhất của biểu thức là 2 đạt được khi x = 5.

Câu hỏi số 6 trang 33 SBT Toán 7 Tập 1: Trong các khẳng định sau, khẳng định nào đúng?

A. Tích của hai số vô tỉ là một số vô tỉ;

B. Tổng của hai số vô tỉ là một số vô tỉ;

C. Tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ;

D. Thương của hai số vô tỉ là một số vô tỉ.

Lời giải:

Đáp án đúng là C

A. Tích của hai số vô tỉ là một số vô tỉ;

Khảng định này sai vì $\sqrt{2}$ là số vô tỉ nhưng tích của $\sqrt{2}$.$\sqrt{2}$ = 2 là số hữu tỉ.

B. Tổng của hai số vô tỉ là một số vô tỉ;

Khẳng định này sai vì $\sqrt{2}$ là số vô tỉ và -$\sqrt{2}$ cũng là số vô tỉnh nhưng $\sqrt{2}$ + (-$\sqrt{2}$ ) = 0 lại là số hữu tỉ.

C. Tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ;

Khẳng định này đúng vì tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ.

D. Thương của hai số vô tỉ là một số vô tỉ.

Khẳng định này sai vì $\sqrt{2}$ là số vô tỉ nhưng $\sqrt{2}$: $\sqrt{2}$ = 1 lại là số hữu tỉ.

Câu hỏi số 7 trang 33 SBT Toán 7 Tập 1: Với mọi số thực x. Khẳng định nào sau đây sai?

A. |x| $\ge$ x;

B. |x| $\ge$-x;

C. |x|² = x²;

D. |x| = x.

Lời giải:

Đáp án đúng là: D

Khẳng định sai là D vì nếu x < 0 thì |x| = -x.

Ví dụ: |-5| = 5.

Câu hỏi số 8 trang 33 SBT Toán 7 Tập 1: Cho x, y là hai số thực tùy ý. Khẳng định nào sau đây là đúng?

A. |x – y| = x – y;

B. | x – y| = |x| – |y|;

C. |x + y| = |x| + |y|;

D. |x + y| = |x| – |y| nếu x > 0 > y và |x| $\ge$ |y|.

Lời giải:

Đáp án đúng là: D

A sai , khi x < y

B sai nếu x = 0 và y khác 0

C sai, chẳng hạn khi x = -y và y khác 0

D đúng, theo quy tắc cộng hai số trái dấu.

Giải SBT Toán 7 trang 34 Tập 1

B – Bài tập

Bài 2.37 trang 34 SBT Toán 7 Tập 1: Bằng cách ước lượng tích, giải thích vì sao kết quả phép nhân sau đây là sai:

6,238.3,91 = 21,390558.

Lời giải:

Làm tròn số 6,238 đến hàng đơn vị ta thu được kết quả là 6. Làm tròn 3,91 đến hàng đơn vị ta thu được kết quả là 4.

Ta có 6,238.3,91 $\approx$6.4 = 24. Nên kết quả của phép tính 6,238.3,91 sẽ gần với 24.

Mà kết quả đề bài cho là 21,390558 rất xa so với 24 nên phép tính sai.

Bài 2.38 trang 34 SBT Toán 7 Tập 1: Giải thích vì sao kết quả phép tính: 28,1 . 1,(8) = 55, 0(7) không đúng.

Lời giải:

Làm tròn số 1,(8) tới hàng đơn vị ta thu được kết quả là 2.

Ta có: 28,1 . 1,(8) $\approx$28,1 . 2 = 56,2. Vậy kết qảu của phép tính phải gần với 56,2 nhưng kết quả đề bài cho lại là 55,0(7) khác xa 56,2. Nên kết quả phép tính đề bài sai.

Bài 2.39 trang 34 SBT Toán 7 Tập 1: Chứng tỏ rằng 0,(3)² = 0, (1).

Lời giải:

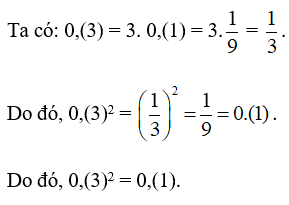
Bài 2.40 trang 34 SBT Toán 7 Tập 1: Viết số 0,1(235) dưới dạng phân số.

Lời giải:

Ta có: 0,1(235) = 1, (235) : 10 = (1 + 0,(235)) : 10

Đặt x = 0,(235) thì 1000x = 235,(235) = 235 + x, suy ra 999x = 23 nên x = $\frac{235}{999}$.

Do đó, 0,1(235) = $\left(1+\frac{235}{999}\right):10=\frac{1234}{9990}$.

Bài 2.41 trang 34 SBT Toán 7 Tập 1: Tính và làm tròn kết quả đến hàng phần nghìn: 2,25 – 2,(3).

Lời giải:

2,25 – 2,(3) = (2 + 0,25) – (2 + 0,(3)) = 2 + 0,25 – 2 – 0,(3) = 0,25 – 0,(3)

Ta có:

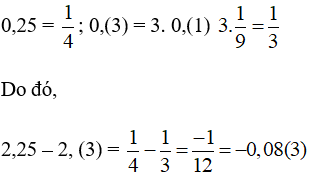
Ta làm tròn kết quả đến hàng phần nghìn thu được kết quả làm tròn là -0,083.

Bài 2.42 trang 34 SBT Toán 7 Tập 1: So sánh a = 1,0(10) và b = 1,(01).

Lời giải:

Vì hai số đều có phần nguyên là 1 giống nhau nên ta đi so sánh phần thập phân của hai số là 0,0(10) và 0,(01).

Đặt x = 0,0(10) và y = 0,(01).

Ta thấy 1000x = 10,(10) = 10 + 0,(10) = 10 + 10x nên 990x = 10. Suy ra x = $\frac{10}{990}=\frac{1}{99}$

Tương tự, 100y = 1,(01) = 1 + y nên 99y = 1. Suy ra y = $\frac{1}{99}$.

Do đó, x = y = $\frac{1}{99}$.

Suy ra, a = b.

Bài 2.43 trang 34 SBT Toán 7 Tập 1: Không dùng máy tính, hãy cho biết số $\sqrt{555555}$ là số hữu tỉ hay vô tỉ.

Lời giải:

Số a = 555 555 có tổng các chữ số bằng 30 và 30 chia 9 dư 3 nên a chia 9 dư 3. Nếu $\sqrt{a}$ là số hữu tỉ thì a phải là số chính phương, tức là a = n² $\left(n\in \mathbb{N}\right)$. Các số chính phương đầu tiên là 0; 4; 9; 16;25; 36;49;64; 81; 100; 121; 144; 169… Khi ta chia các số này cho 9 ta thấy các số dư lần lượt là 0; 4; 0; 7; 7; 1; 0; 4; 0; 7;… Các số dư tuần hoàn với chu kỳ là 0; 4; 0; 7; 7; 1. Như vậy các số chính phương khi chia cho 9 không bao giờ có dư 3. Từ đó, a= 555 555 không phải số chính phương nên $\sqrt{555555}$ là số vô tỉ.

Bài 2.44 trang 34 SBT Toán 7 Tập 1: Không dùng máy tính, hãy cho biết số $\sqrt{\mathrm{11...1}}$ (101 chữ số 1) là số hữu tỉ hay vô tỉ. Giải thích.

Lời giải:

Ta có 11…1 có 101 chữ số 1 nên tổng các chữ số của nó bằng 101.

Vì 101 chia cho 3 dư 2 nên 11...1 (101 số 1) chia cho 3 cũng dư 2.

Mặt khác, bình phương của một số tự nhiên chỉ có thể chia hết cho 3 hoặc chia 3 dư 1 nên 11…1 (101 chữ số 1) không phải số chính phương. Vì vậy $\sqrt{\mathrm{11...1}}$ là số vô tỉ.

Bài 2.45 trang 34 SBT Toán 7 Tập 1: Giả sử x, y là hai số thực đã cho. Biết |x| = a và |y| = b. Tính |xy| theo a và b.

Lời giải:

+) Nếu x, y $\ge 0$ thì xy $\ge 0$ và x = |x| = a; y = |y| = b; |xy| = xy = ab.

Do đó, |xy| = ab.

+) Nếu x, y < 0 thì xy > 0 và x = -|x| = -a; y = -|y| = -b ; |xy| = (-a).(-b) = ab.

Do đó, |xy| = ab.

+) Nếu x, y trái dấu, ví dụ x > 0 và y < 0 thì x.y < 0

Nên |xy| = -xy = (-a).(-b) = ab.

Bài 2.46 trang 34 SBT Toán 7 Tập 1: Sử dụng tính chất |a + b| $\le$|a| + |b| (Bài tập 2.36), giải thích vì sao không có số thực x nào thỏa mãn |x – 1| + |x – 3| = $\sqrt{2}$.

Lời giải:

Ta có: |x – 1| + | x – 3| = |x – 1| + |3 – x| $\ge$ |(x – 1) + (3 – x)| = |x – 1 + 3 – x| = |2| = 2

Vì  x – 1| + | x – 3| = |x – 1| + |3 – x| $\ge$ 2 mà 2 > $\sqrt{2}$ nên không có số thực nào thỏa mãn |x – 1| + |x – 3| = $\sqrt{2}$.

Bài 2.47 trang 34 SBT Toán 7 Tập 1: Chứng minh rằng |x| + |x – 2| + |x – 4| $\ge$ 4 đúng với mọi số thực x.

Lời giải:

Ta có: |x | + |x – 4| = |x| + |4 – x| $\ge$| x + (4 – x)| = |x + 4 – x| = |4|

Lại có: |x – 2| $\ge$0 nên |x| + |x – 2| + |x – 4| $\ge$4 (điều phải chứng minh).

Bài 2.48 trang 34 SBT Toán 7 Tập 1: Tích của một số vô tỉ với một số nguyên dương là số hữu tỉ hay vô tỉ? Hãy giải thích tại sao có vô số số vô tỉ.

Lời giải:

Giả sử x là một số vô tỉ và n là một số nguyên dương. Nếu tích nx là số hữu tỉ thì x = $\frac{nx}{n}$ là số hữu tỉ (thương của hai số hữu tỉ là một số hữu tỉ), trái với giả thiết x là số vô tỉ. Vậy nx phải là số vô tỉ.

Như vậy, $\sqrt{2};2\sqrt{2};3\sqrt{2}\mathrm{...}$ đều là số vô tỉ, do đó có vô số số vô tỉ.

Bài 2.49 trang 34 SBT Toán 7 Tập 1: Trong các kết luận sau đây, kết luận nào đúng, kết luận nào sai?

a) Tổng của hai số vô tỉ là một số vô tỉ.

b) Tổng của hai số vô tỉ dương là một số vô tỉ.

c) Tổng của hai số vô tỉ âm là một số vô tỉ.

Lời giải:

a) Tổng của hai số vô tỉ là một số vô tỉ.

Kết luận này sai vì $\sqrt{5}$ là số vô tỉ và -$\sqrt{5}$ nhưng $\sqrt{5}$ + (-$\sqrt{5}$) = 0 là số hữu tỉ.

b) Tổng của hai số vô tỉ dương là một số vô tỉ.

Khẳng định này sai vì $\sqrt{2}$ và 5 - $\sqrt{2}$ là các số vô tỉ dương nhưng tổng của chúng $\sqrt{2}$ + (5 - $\sqrt{2}$) = $\sqrt{2}$ + 5 - $\sqrt{2}$ = 5 là một số hữu tỉ

c) Tổng của hai số vô tỉ âm là một số vô tỉ.

Khảng định này sai vì -$\sqrt{2}$ và -5 + $\sqrt{2}$ là các số vô tỉ âm nhưng (-$\sqrt{2}$) + (-5 + $\sqrt{2}$) = -$\sqrt{2}$ + (-5) + $\sqrt{2}$ = -5 là một số hữu tỉ.

Giải SBT Toán 7 trang 35 Tập 1

Bài 2.50 trang 35 SBT Toán 7 Tập 1: Cho một hình vuông có cạnh bằng 5 đơn vị và cho 76 điểm nằm bên trong hình vuông đó. Chứng tỏ rằng có một hình tròn với bán kính bằng $\frac{3}{4}$ đơn vị chứa trọn 4 trong số 76 điểm đã cho.

Lời giải:

Chia hình vuông đã cho thành 25 hình vuông nhỏ có cạnh bằng 1. Nếu trong mỗi hình vuôn nhỏ có không quá ba điểm (trong số các điểm đã cho) thì trong hình vuông lớn có không quá 25.3 = 75 (điểm), trái với giả thiết trong hình vuông lớn có 76 điểm. Như vậy, có ít nhất một hình vuông nhỏ (cạnh bằn 1) chưa bốn điểm (trong các điểm đã cho). Hình tròn với đường kính là đường chéo của hình vuông nhỏ này chứa toàn bộ hình vuông nhỏ và có bán kính $\frac{\sqrt{2}}{2}<\frac{3}{4}$.

Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc

Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết

Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song

Bài 11: Định lí và chứng minh định lí

Ôn tập chương 2

Xem thêm tài liệu Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Ôn tập chương 2