Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 7 Bài 36 (Kết nối tri thức): Hình hộp chữ nhật và hình lập phương

    Với giải sách bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 36.

    1 1,517 02/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải sách bài tập Toán lớp 7 Bài 36: Hình hộp chữ nhật và hình lập phương

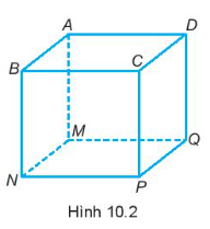
    Bài 10.1 trang 62 SBT Toán 7 Tập 2: Gọi tên các đỉnh, cạnh, đường chéo, mặt của hình lập phương trong Hình 10.2.

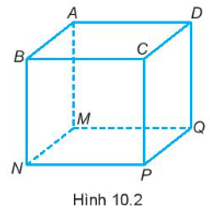
    Sách bài tập Toán 7 Bài 36 (Kết nối tri thức): Hình hộp chữ nhật và hình lập phương (ảnh 1)

    Lời giải:

    Sách bài tập Toán 7 Bài 36 (Kết nối tri thức): Hình hộp chữ nhật và hình lập phương (ảnh 1)

    Quan sát hình lập phương trong Hình 10.2, ta có:

    - Các đỉnh: A, B, C, D, M, N, P, Q;

    - Cạnh: AB, BC, CD, DA, MN, NP, PQ, QM, AM, DQ, CP, BN;

    - Các đường chéo: AP, BQ, CM, DN;

    - Các mặt: ABCD, MNPQ, ABMN, BCPN, CDQP, DAMQ.

    Bài 10.2 trang 63 SBT Toán 7 Tập 2: Hộp đựng khối rubik có dạng là một hình lập phương có cạnh 3 cm, được làm bằng bìa cứng. Tính thể tích của chiếc hộp và diện tích bìa cứng để làm chiếc hộp đó.

    Lời giải:

    Thể tích của chiếc hộp đựng là:

    V = 33 = 27 (cm3)

    Diện tích bìa cứng để làm một mặt của chiếc hộp đó là:

    S = 32 = 9 (cm2)

    Diện tích bìa cứng để làm chiếc hộp hình lập phương đó là:

    6 . 9 = 54 (cm2).

    Vậy thể tích của chiếc hộp và diện tích bìa cứng để làm chiếc hộp là 54 cm2.

    Bài 10.3 trang 63 SBT Toán 7 Tập 2: Một cái bể chứa nước có dạng hình hộp chữ nhật dài 2 m, rộng 1,5 m, cao 1,2 m. Lúc đầu bể chứa đầy nước, sau đó người ta lấy ra 45 thùng nước, mỗi thùng 20 lít. Hỏi sau khi lấy nước ra, mực nước trong bể cao bao nhiêu?

    Lời giải:

    Thể tích của bể chứa là:

    V = 2 . 1,5 . 1,2 = 3,6 (m3).

    Đổi: 3,6 m3 = 3 600 dm3 = 3 600 ?

    Lượng nước được lấy ra khỏi bể là:

    20 . 45 = 900 (?).

    Sau khi lấy nước ra, lượng nước còn lại trong bể là:

    3 600 − 900 = 2 700 (?).

    Đổi: 2 700 ? = 2,7 m3.

    Diện tích của đáy bể là:

    2 . 1,5 = 3 (m2).

    Mực nước trong bể cao là:

    2,7 : 3 = 0,9 (m).

    Vậy sau khi lấy nước ra, mực nước trong bể cao 0,9 m.

    Bài 10.4 trang 63 SBT Toán 7 Tập 2: Tính thể tích của một hình lập phương, biết tổng diện tích các mặt của nó là 216 cm2.

    Lời giải:

    Do tổng diện tích các mặt của một hình lập phương là 216 cm2 nên diện tích một mặt của hình lập phương là:

    216 : 6 = 36 (cm2)

    Gọi độ dài cạnh hình lập phương là a (cm).

    Khi đó diện tích một mặt của hình lập phương là a2 (cm2).

    Ta có: a2 = 36 nên a = 6 (cm).

    Vậy độ dài cạnh của hình lập phương đó là: 6 (cm).

    Thể tích của hình lập phương là:

    V = a3 = 63 = 216 (cm3).

    Vậy thể tích của hình lập phương đã cho là 216 cm3.

    Bài 10.5 trang 63 SBT Toán 7 Tập 2: Một bể nước dạng hình hộp chữ nhật có chiều dài 2 m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước trong bề cao 0,8 m.

    a) Tính chiều rộng của bể nước.

    b) Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể nước cao bao nhiêu mét?

    Lời giải:

    a) Thể tích lượng nước được đổ vào bể là:

    V1 = 120 . 20 = 2 400 (?).

    Đổi 2 400 ? = 2 400 dm3 = 2,4 (m3).

    Khi đó, mực nước trong bể cao 0,8 m nên ta tính được diện tích mặt đáy của bể là:

    Sđáy = 2,4 : 0,8 = 3 (m2).

    Chiều rộng của bể nước hình hộp chữ nhật là:

    3 : 2 = 1,5 (m).

    Vậy chiều rộng của bể nước là 1,5 m.

    b) Sau khi đổ thêm 60 thùng nước nữa thì tổng số thùng nước đã đổ vào là:

    120 + 60 = 180 (thùng).

    Lượng nước khi đầy bể cũng chính là thể tích của bể nước là:

    V = 180 . 200 = 3 600 (?).

    Đổi 3 600 ? = 3 600 dm3 = 3,6 (m3).

    Do ta đã tính được diện tích mặt đấy của bể nước là: Sđáy = 3 (m2)

    Chiều cao của bể là:

    3,6 : 3 = 1,2 (m).

    Vậy chiều cao của bể là 1,2 m.

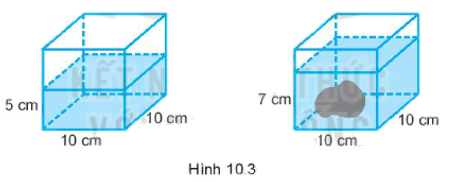
    Bài 10.6 trang 63 SBT Toán 7 Tập 2: Bạn Hà có một bể cá có dạng hình lập phương có độ dài cạnh 10 cm. Ban đầu nước trong bể có độ cao 5 cm. Bạn Hà bỏ thêm vào trong bể một hòn đá trang trí chìm trong nước thì nước trong bể có độ cao 7 cm (H.10.3). Hỏi hòn đá bạn Hà bỏ vào bể có thể tích bao nhiêu cm3?

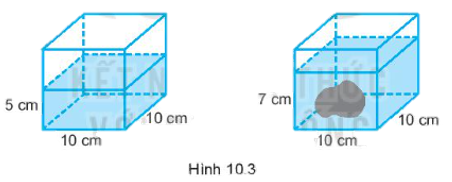
    Sách bài tập Toán 7 Bài 36 (Kết nối tri thức): Hình hộp chữ nhật và hình lập phương (ảnh 1)

    Lời giải:

    Sách bài tập Toán 7 Bài 36 (Kết nối tri thức): Hình hộp chữ nhật và hình lập phương (ảnh 1)

    Tổng thể tích của lượng nước có trong bể và hòn đá là:

    V1 = 10 . 10 . 7 = 700 (cm3)

    Thể tích lượng nước trong bể ban đầu là:

    V2 = 10 . 10 . 5 = 500 (cm3)

    Thể tích của hòn đá bạn Hà đã bỏ vào bể là:

    V = V1 – V2 = 700 – 500 = 200 (cm3)

    Vậy hòn đá bạn Hà bỏ vào bể có thể tích 200 cm3.

    Bài 10.7 trang 63 SBT Toán 7 Tập 2: Một bể nước hình hộp chữ nhật có kích thước đáy là 2 m × 3 m chưa có nước. Mở vòi nước chảy vào bể trong 8 giờ, mỗi giờ vòi chảy được 500 lít nước. Hỏi khi đó mực nước trong bể cao bao nhiêu mét?

    Lời giải:

    Đổi: 500 ? = 500 dm3 = 0,5 m3.

    Diện tích mặt đáy của bể nước hình hộp chữ nhật là:

    2 × 3 = 6 (m2)

    Lượng nước vòi chảy vào bể trong 8 giờ là:

    0,5.8 = 4 (m3)

    Khi đó, mực nước trong bể có chiều cao là: 4:6=23   m

    Vậy mực nước trong bể cao 23  m.

    Bài 10.8 trang 63 SBT Toán 7 Tập 2: Tính thể tích của hình hộp chữ nhật biết nó có diện tích xung quanh là 10 000 cm2, chiều cao bằng 50 cm và chiều dài hơn chiều rộng 12 cm.

    Lời giải:

    Chu vi mặt đáy của hình hộp chữ nhật là:

    10 000 : 50 = 200 (cm)

    Nửa chu vi mặt đáy của hình hộp chữ nhật là:

    200 : 2 = 100 (cm)

    Khi đó tổng chiều dài và chiều rộng của mặt đáy của hình hộp chữ nhật là 100 cm.

    Chiều dài của hình hộp chữ nhật là:

    (100 + 12) : 2 = 56 (cm)

    Chiều rộng của hình hộp chữ nhật là:

    100 – 56 = 44 (cm)

    Thể tích của hình hộp chữ nhật là:

    V = 56 . 44 . 50 = 123 200 (cm3).

    Vậy thể tích của hình hộp chữ nhật là 123 200 cm3.

    Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Kết nối tri thức hay, chi tiết nhất:

    Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

    Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

    Ôn tập chương 9

    Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

    Ôn tập chương 10

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,517 02/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: