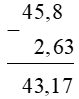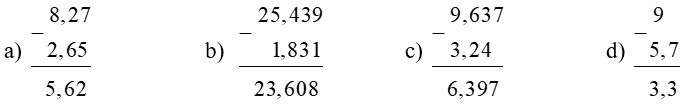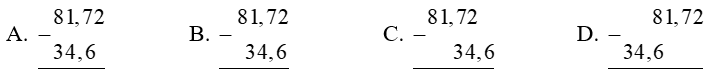Lý thuyết Trừ hai số thập phân (mới 2024 + Bài Tập) - Toán lớp 5
Tóm tắt nội dung chính bài Trừ hai số thập phân lớp 5 môn Toán gồm lý thuyết ngắn gọn, các dạng bài tập về Trừ hai số thập phân điển hình và các ví dụ minh họa giúp học sinh nắm vững kiến thức từ đó biết cách làm bài tập Trừ hai số thập phân Toán lớp 5.
Lý thuyết Trừ hai số thập phân
I. Lý thuyết
Muốn trừ hai số thập phân ta làm như sau:
- Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng thẳng cột với nhau.
- Trừ như trừ các số tự nhiên.
- Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
Chú ý:
● Nếu số chữ số ở phần thập phân của số bị trừ ít hơn số chữ số ở phần thập phân của số trừ thì ta có thể viết thêm một số thích hợp (chữ số 0) vào bên phải phần thập phân của số bị trừ rồi trừ như trừ các số tự nhiên.
●a – b – c = a – (b + c)
Ví dụ 1: Đặt tính rồi tính:
a) 6,82 – 4,35
b) 37,586 – 8,391
c) 45,8 – 2,63
Hướng dẫn giải
c) Ta có 45,8 = 45,80 nên ta đặt tính được như sau:
Ví dụ 2:
a) 12,56 – (2,56 + 2,6)
= 12,56 – 2,56 – 2,6
= 10 – 2,6
= 7,4
b) 25,8 – 3,3 – 1,7
= 25,8 – (3,3 + 1,7)
= 25,8 – 5
= 20,8
II. Bài tập minh họa
Bài 1. Đặt tính rồi tính
|
a) 8,27 – 2,65 |
b) 25,439 – 1,831 |
c) 9,637 – 3,24 |
d) 9 – 5,7 |
Hướng dẫn giải
Bài 2. Tính.
|
a) 8,3 + 2,7 – 3,5 |
b) 15,62 – 5,02 + 4,8 |
c) 20,8 – 7,4 – 6,2 |
Hướng dẫn giải
a) 8,3 + 2,7 – 3,5
= 11 – 3,5
= 7,5
b) 15,62 – 5,02 + 4,8
= 10,6 + 4,8
= 15,4
c) 20,8 – 7,4 – 6,2
= 13,4 – 6,2
= 7,2
Bài 3. Tính bằng cách thuận tiện.
a) 23,96 – (3,96 + 12,5)
b) 45,7 – 4,5 – 5,5
c) 34,6 + 22,5 + 15,4
Hướng dẫn giải
a) 23,96 – (3,96 + 12,5)
= 23,96 – 3,96 – 12,5
= (23,96 – 3,96) – 12,5
= 20 – 12,5
= 7,5
b) 45,7 – 4,5 – 5,5
= 45,7 – (4,5 + 5,5)
= 45,7 – 10
= 35,7
c) 34,6 + 22,5 + 15,4
= (34,6 + 15,4) + 22,5
= 50 + 22,5
= 72,5
Bài 4.Số?
|
a) 2,65 + .?. = 14,79 |
b) 32,27 – .?. = 14,65 |
Hướng dẫn giải
|
a) 2,65 + 12,14 = 14,79 |
b) 32,27 – 17,62 = 14,65 |
Giải thích chi tiết:
a) Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
14,79 – 2,65 = 12,14
Vậy 2,65 + 12,14 = 14,79
b) Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
32,27 – 14,65 = 17,62
Vậy 32,27 – 17,62 = 14,65
Bài 5.Ba bao thóc cân nặng 150 kg. Bao thứ nhất cân nặng 46,5 kg, bao thứ hai nhẹ hơn bao thứ nhất 4,8 kg. Hỏi bao thứ ba cân nặng bao nhiêu ki-lô-gam?
Hướng dẫn giải
Bài giải
Bao thứ hai nặng số ki-lô-gam là:
46,5 – 4,8 = 41,7 (kg)
Bao thứ nhất và bao thứ hai nặng số ki-lô-gam là:
46,5 + 41,7 = 88,2 (kg)
Bao thứ ba cân nặng số ki-lô-gam là:
150 – 88,2 = 61,8 (kg)
Đáp số: 61,8 ki-lô-gam.
III. Bài tập vận dụng
Bài 1. Cho phép tính 81,72 – 34,6. Cách đặt tính đúng là:
Bài 2. Chọn dấu thích hợp để điền vào chỗ chấm:
36,21 – 23,74 ..... 8,6 + 3,87
A. = B. > C. < D. A, B, C đều sai
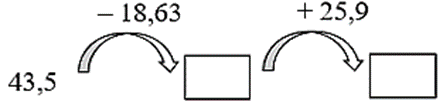
Bài 3. Các số thích hợp điền vào ô trống lần lượt là:
A. 24,87 và 50,77 B. 62,13 và 88,03 C. 24,87 và 50,77 D. 62,13 và 88,03
Bài 4. Đặt tính rồi tính
|
a) 5,23 – 3,76 |
b) 82,74 – 9,45 |
c) 75,238 – 12,48 |
d) 34 – 17,29 |
Bài 5. Tính.
|
a) 12,48 + 43,7 – 36,5 |
b) 62,3 – 12,81 + 3,5 |
c) 34,89 – 12,08 – 5,8 |
Bài 6. Tính bằng cách thuận tiện.
a) 21,3 + 38,9 + 28,7
b) 89,27 – (9,27 + 6,5)
c) 48,23 – 24,14 – 5,86
Bài 7.Số?
|
a) 13,29 + .?. = 34,89 |
b) 72,35 – .?. = 41,28 |
Bài 8. Một tấm vải dài 49m. Lần thứ nhất bán 12,5m; lần thứ hai bán 17,6m. Hỏi sau hai lần bán tấm vải còn lại dài bao nhiêu mét?
Bài 9. Một đội công nhân cần sửa 3,6 km đường trong 3 ngày. Ngày thứ nhất đội sửa được 0,9 km đường. Ngày thứ hai sửa được nhiều hơn ngày thứ nhất 0,6 km đường. Hỏi ngày thứ ba đội cần sửa bao nhiêu ki-lô-mét đường nữa để xong công việc?
Bài 10. Đường gấp khúc ABC dài 5,27 m, trong đó đoạn thẳng AB dài 2,18 m. Hỏi đoạn thẳng BC dài bao nhiêu mét?
Xem thêm các chương trình khác: