Lý thuyết Thể tích hình hộp chữ nhật (mới 2024 + Bài Tập) - Toán lớp 5

Lý thuyết Thể tích hình hộp chữ nhật

I. Lý thuyết

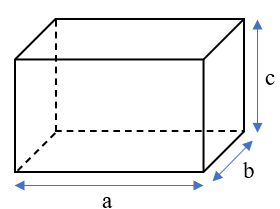
Muốn tính thể tích hình hộp chữ nhật, ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo)

V = a × b × c

(a, b, c là ba kích thước của hình hộp chữ nhật)

Ví dụ: Tính thể tích hình hộp chữ nhật có chiều dài 4 cm, chiều rộng 5 cm và chiều cao 6 cm.

Thể tích hình hộp chữ nhật đó là:

4 × 5 × 6 = 120 (cm³)

Đáp số: 120 cm³

Ví dụ: Tìm chiều cao hình hộp chữ nhật biết thể tích là 10 cm³, chiều dài 4 cm, chiều rộng 5 cm.

Chiều cao của hình hộp chữ nhật đó là:

10 : 4 : 5 = 0,2 (cm)

Đáp số: 0,2 cm

II. Bài tập minh họa

Bài 1. Tìm kích thước còn thiếu của hình hộp chữ nhật thể tích V, chiều dài a, chiều rộng b, chiều cao c:

a) V = 120 m³, a = 4 m, b = 3 m.

b) V = 36 cm³, b = 2,5 cm, c = 3,6 cm.

c) V = 13,5 dm³, a = 5 dm, c = 3 dm.

d) V = 50,286 m³, a = 5,1 m, b = 2,9 m.

Hướng dẫn giải:

a) Chiều cao của hình hộp chữ nhật đó là: 120 : 4 : 3 = 10 (m)

b) Chiều dài của hình hộp chữ nhật đó là: 36 : 2,5 : 3,6 = 4 (cm)

c) Chiều rộng của hình hộp chữ nhật đó là: 13,5 : 5 : 3 = 0,9 (dm)

d) Chiều cao của hình hộp chữ nhật đó là: 50,286 : 5,1 : 2,9 = 3,4 (m)

Bài 2. Tính thể tích của hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c:

a) a = 5 cm, b = 4 cm, c = 10 cm

b) a = 8 m, b = 20 dm, c = 900 cm

c) a = 5,4 dm, b = 4,7 dm, c = 60 cm

Hướng dẫn giải:

a) Thể tích hình hộp chữ nhật đó là: 5 × 4 × 10 = 200 (cm³)

b) Đổi: 20 dm = 2 m, 900 cm = 9 m

Thể tích hình hộp chữ nhật đó là: 8 × 2 × 9 = 144 (m³)

c) Đổi: 60 cm = 6 dm

Thể tích hình hộp chữ nhật đó là: 5,4 × 4,7 × 6 = 152,28 (dm³)

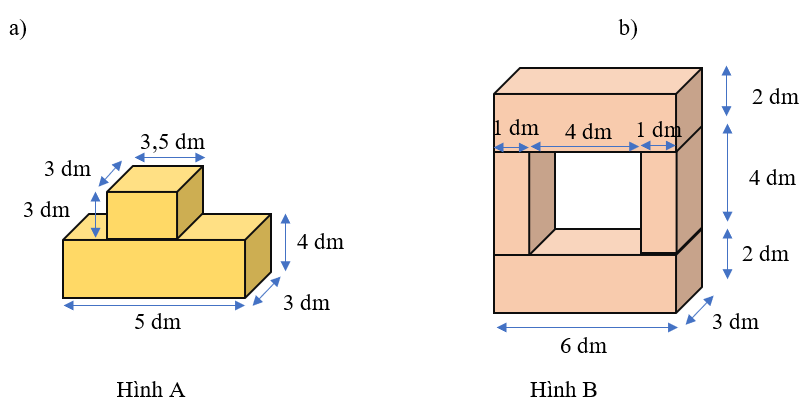
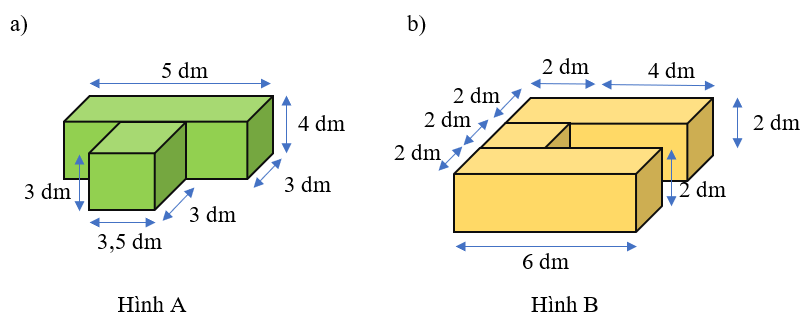
Bài 3. Tính thể tích của mỗi hình sau:

Hướng dẫn giải:

a)

Chia nhỏ hình A ra thành 2 hình hộp chữ nhật:

+ Hình hộp chữ nhật bên dưới có kích thước lần lượt là 5 dm, 3 dm, 4 dm

+ Hình hộp bên trên có kích thước lần lượt là 3 dm, 3,5 dm, 3 dm

Thể tích hình hộp chữ nhật bên dưới là:

5 × 3 × 4 = 60 (dm³)

Thể tích hình hộp chữ nhật bên trên là:

3 × 3,5 × 3 = 31,5 (dm³)

Thể tích của hình A là:

60 + 31,5 = 91,5 (dm³)

Đáp số: 91,5 dm³

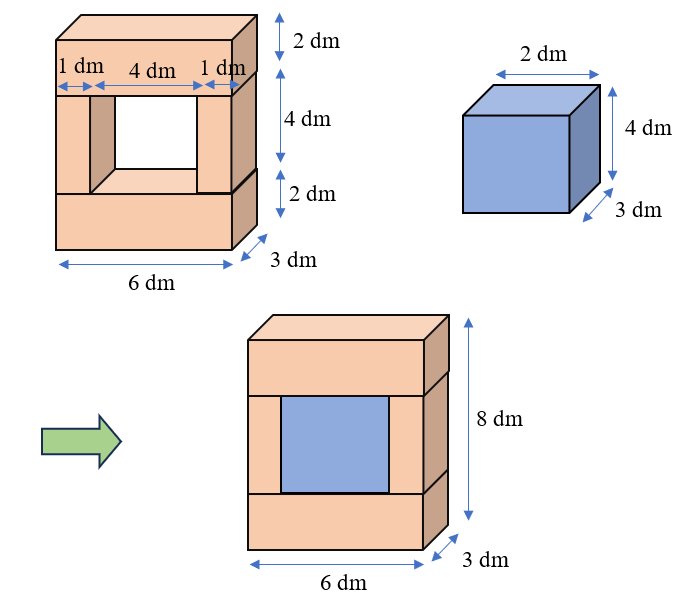
b)

Thêm vào hình B một hình hộp chữ nhật đã bị khuyết ở giữa có kích thước lần lượt là 4 dm, 3 dm, 4 dm để ta một hình hộp chữ nhật to có kích thước lần lượt là 6 dm, 3 dm, 8 dm.

Hướng dẫn giải:

Thể tích của hình chữ nhật to là:

6 × 3 × 8 = 144 (dm³)

Thể tích hình hộp chữ nhật thêm vào là:

4 × 3 × 4 = 48 (dm³)

Thể tích của hình B là:

144 - 48 = 96 (dm³)

Đáp số: 96 dm³

Bài 4. Một máy bơm nước mỗi giờ bơm được 1 200 lít nước vào bể chứa. Hỏi để máy bơm nước đó bơm nước đầy vào bể hình hộp chữ nhật có kích thước 4 m, 5 m, 1,2 m cần thời gian bao nhiêu lâu?

Hướng dẫn giải:

Thể tích bể là:

4 × 5 × 1,2 = 24 (m³)

Đổi: 24 m³ = 24 000 dm³ = 24 000 lít

Thời gian máy bơm nước bơm đầy bể chứa là:

24 000 : 1 200 = 20 (giờ)

Đáp số: 20 giờ

Bài 5. Một bể nước hình hộp chữ nhật có chiều dài 2 m. Lúc đầu bể không có nước. Sau khi đổ vào bể 100 thùng nước thì mực nước trong bể là 1 m. Biết mỗi thùng chứa 20 lít nước.

a) Tính chiều rộng của bể nước.

b) Người ta đổ thêm vào bể 20 thùng nước nữa thì mực nước trong bể là bao nhiêu?

Hướng dẫn giải:

a)

Thể tích nước trong bể là:

100 × 20 = 2 000 (lít)

Đổi: 2 000 lít = 2 m³

Chiều rộng của bể nước là:

2 : 2 : 1 = 1 (m)

Đáp số: 1 m

b)

Người ta đổ tất cả số thùng nước là:

100 + 20 = 120 (thùng)

Mực nước khi đổ 1 thùng là:

1 : 100 = 0,01 (m)

Sau khi đổ thêm mực nước trong bể là:

0,01 × 120 = 1,2 (m)

Đáp số: 1,2 m

III. Bài tập vận dụng

Bài 1. Tính thể tích của hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c:

a) a = 2,6 cm, b = 3,7 cm, c = 3 cm

b) a = 4 dm, b = 5 dm, c = 3 dm

c) a = 1,5 m, b = 12 dm, c = 369 cm

Bài 2. Tìm kích thước còn thiếu của hình hộp chữ nhật thể tích V, chiều dài a, chiều rộng b, chiều cao c:

a) V = 26,88 m³, a = 3,5 m, b = 6,4 m.

b) V = 64 dm³, a = 8 dm, c = 4 dm.

c) V = 14,21 m³, a = 2,9 m, b = 1,4 m.

Bài 3. Chọn ý đúng. Công thức tính thể tích của một hình hộp chữ nhật có kích thước chiều dài m, chiều rộng n và chiều cao p là:

A. V = (m + n + p) × 2

B. V = (m + n) × 2 × p

C. V = (m × n) × p

D. V = (p - n) × 2 × n

Bài 4. Tính thể tích của mỗi hình sau:

Bài 5. Tính thể tích của mỗi đồ vật sau:

Bài 6. Tính thể tích của mỗi hình sau:

Bài 7. Một hình hộp chữ nhật có chu vi đáy là 54 m, chiều rộng bằng $\frac{4}{5}$ chiều dài. Biết chiều cao của hình hộp chữ nhật là 10 m. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật.

Bài 8. Một bể cá dạng hình hộp chữ nhật có chiều dài 0,9 m, chiều rộng là 0,6 m và chiều cao 0,75 m. Mực nước ban đầu trong bể cao 25cm. Người ta cho vào bể một hòn đá có thể tích 16,2 dm³. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng-ti-mét?

Bài 9. Một vòi nước mỗi giờ chảy được 400 lít nước vào bể. Hỏi để vòi nước đó chảy đầy nước vào bể hình hộp chữ nhật có kích thước 1,2 m; 3,5 m; 2 m cần thời gian bao nhiêu lâu?

Bài 10. Một bể cá có dạng hình hộp chữ nhật có chiều dài 2,5 m; chiều rộng 1,2 m; chiều cao 2 m. Ban đầu bể không có nước, người ta đã đổ một lượng nước vào bể. Biết mực nước trong bể bằng $\frac{7}{10}$ chiều cao của bể. Hỏi người ta đã đổ bao nhiêu lít nước vào bể?