Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật (mới 2024 + Bài Tập) - Toán lớp 5

Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

I. Lý thuyết

1. Diện tích xung quanh

Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.

Muốn tính diện tích xung quanh của hình hộp chữ nhật, ta có thể lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

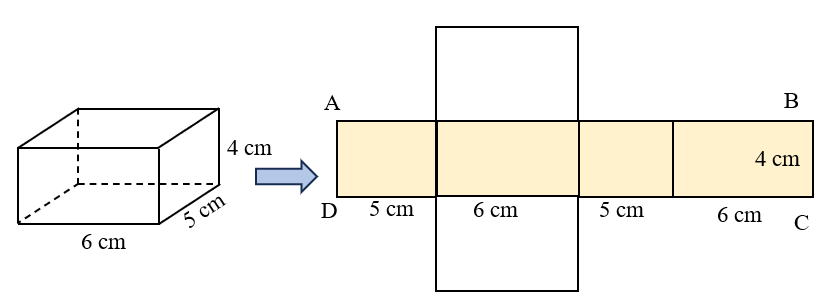
Ví dụ: Tính diện tích xung quanh của hình hộp chữ nhật có chiều dài 6 cm, chiều rộng 5 cm và chiều cao 4 cm.

Chu vi của mặt đáy là:

(6 + 5) × 2 = 22 (cm)

Diện tích xung quanh của hình hộp chữ nhật là:

22 × 4 = 88 (cm²)

Đáp số: 88 cm²

2. Diện tích toàn phần

Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích sáu mặt của hình hộp chữ nhật.

Muốn tính diện tích toàn phần của hình hộp chữ nhật, ta có thể lấy diện tích xung quanh cộng với diện tích hai mặt đáy.

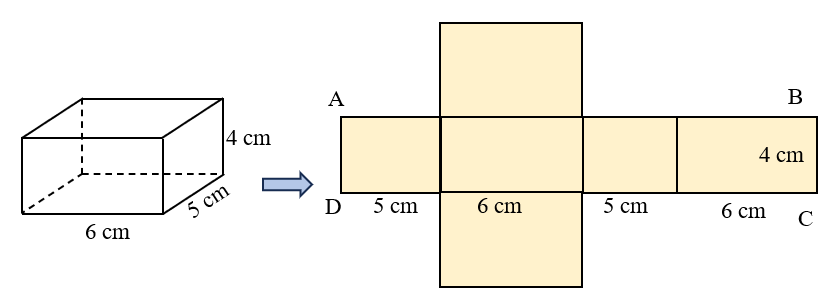
Ví dụ: (Lấy ví dụ trên) Tính diện tích toàn phần của hình hộp chữ nhật có chiều dài 6 cm, chiều rộng 5 cm và chiều cao 4 cm.

Diện tích đáy của hình hộp chữ nhật là:

6 × 5 = 30 (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

88 + 30 × 2 = 148 (cm²)

Đáp số: 148 cm²

II. Bài tập minh họa

Bài 1. Hoàn thành bảng sau:

Hình hộp chữ nhật	Chiều dài	5 m	10, 8 dm	1 m
	Chiều rộng	4 m	8,9 dm	5 dm
	Chiều cao	3 m	7,1 dm	89 cm
	Diện tích xung quanh
	Diện tích toàn phần

Hướng dẫn giải:

Hình hộp chữ nhật	Chiều dài	5 m	10, 8 dm	1 m
	Chiều rộng	4 m	8,9 dm	5 dm
	Chiều cao	3 m	7,1 dm	89 cm
	Diện tích xung quanh	54 m2	279,74 dm2	26700 cm2
	Diện tích toàn phần	128 m2	655,6 dm2	58400 cm2

Bài 2. Bạn An dùng tờ giấy gói quà để gói hộp quà hình chữ nhật có chiều dài 12 cm, chiều rộng 10 cm, chiều cao 7 cm. Hỏi diện tích của tờ giấy gói là bao nhiêu xăng-ti-mét? Biết bạn An dùng hết một tờ giấy gói đó.

Hướng dẫn giải:

Diện tích của tờ giấy bằng diện tích 6 mặt của hình hộp chữ nhật (diện tích toàn phần)

Chu vi mặt đáy của hộp quà đó là:

(12 + 10) × 2 = 44 (cm)

Diện tích xung quanh của hộp quà đó là:

44 × 7 = 308 (cm²)

Diện tích mặt đáy của hộp quà đó là:

12 × 10 = 120 (cm²)

Diện tích toàn phần của hộp quà đó là:

308 + 120 × 2 = 548 (cm²)

Vậy: Diện tích của tờ giấy đó là: 548 cm²

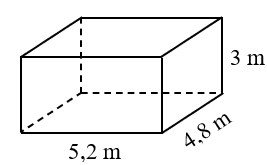
Bài 3. Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 5,2 m, chiều rộng 4,8 m và chiều cao 3 m.

Hướng dẫn giải:

Chu vi mặt đáy của hình hộp chữ nhật là:

(5,2 + 4,8) × 2 = 20 (m)

Diện tích xung quanh của hình hộp chữ nhật là:

20 × 3 = 60 (m²)

Diện tích mặt đáy của hình hộp chữ nhật là:

5,2 × 4,8 = 24,96 (m²)

Diện tích toàn phần của hình hộp chữ nhật là:

60 + 24,96 × 2 = 109,92 (m²)

Đáp số: Diện tích xung quanh: 60 m²

Diện tích toàn phần: 109,92 m²

Bài 4. Bạn Hùng giúp bố sơn bên ngoài một cái thùng không nắp hình hộp chữ nhật có chiều dài 2 m, chiều rộng 10 dm, chiều cao 90 cm. Tính diện tích phần bạn Hùng có thể sơn được của cái thùng đó?

Hướng dẫn giải:

Vì cái thùng không nắp nên thùng hình hộp chữ nhật đó có 5 mặt với 4 mặt bên và 1 mặt đáy. Diện tích bạn Hùng có thể sơn được bằng tổng diện tích xung quanh và một mặt đáy.

Đổi: 2 m = 200 cm, 10 dm = 100 cm

Chu vi mặt đáy của cái thùng đó là:

(200 + 100) × 2 = 600 (cm)

Diện tích xung quanh của cái thùng đó là:

600 × 90 = 54 000 (cm²)

Diện tích mặt đáy của cái thùng đó là:

200 × 100 = 20 000 (cm²)

Diện tích phần bạn Hùng có thể sơn được là:

54 000 + 20 000 = 74 000 (cm²)

Đáp số: 74 000 cm²

Bài 5. Hình A dưới đây được tạo ra bởi năm hình hộp chữ nhật bằng nhau, mỗi hình có chiều dài 3 dm, chiều rộng 2 dm và chiều cao 1 dm. Tính diện tích toàn phần của hình A.

Hình A

Hướng dẫn giải:

Chiều dài của hình A là:

3 × 5 = 15 (dm)

Chu vi mặt đáy của hình A là:

(15 + 2) × 2 = 34 (dm)

Diện tích xung quanh của hình A là:

34 × 1 = 34 (dm²)

Diện tích mặt đáy của hình A là:

15 × 2 = 30 (dm²)

Diện tích toàn phần của hình A là:

34 + 30 × 2 = 94 (dm²)

Đáp số: 94 dm²

III. Bài tập vận dụng

Bài 1. Chọn ý đúng. Hình hộp chữ nhật có chiều dài là a, chiều rộng là b và chiều cao là c. Diện tích xung quanh của hình hộp chữ nhật đó là:

A. (a × b) × 2 × c  B. (a + b) + 2 × c  C. (a + b) × 2 × c  D. (a × b) × 2 + c

Bài 2. Chọn ý đúng. Hình hộp chữ nhập có diện tích xung quanh là a, chu vi đáy là b, chiều rộng là c.

a) Chiều dài đáy của hình hộp chữ nhật đó là:

A. b : 2 – c    B. a : b : 2    C. a : c – b    D. b – c

b) Chiều cao của hình hộp chữ nhật đó là:

A. a × c    B. b × c    C. a : c    D. a : b

Bài 3. Hoàn thành bảng sau:

Hình hộp chữ nhật	Chiều dài	5 m	10, 8 dm	1 m
	Chiều rộng	4 m	8,9 dm	5 dm
	Chiều cao	3 m	7,1 dm	89 cm
	Diện tích xung quanh
	Diện tích toàn phần

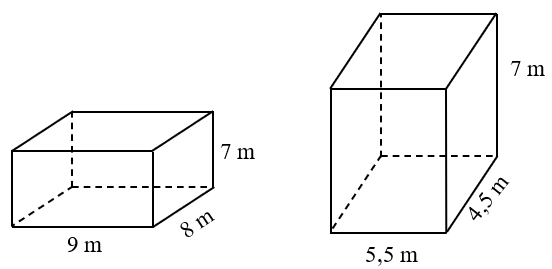
Bài 4. Tính diện tích toàn phần của các hình sau:

Bài 5. Một viên gạch dạng hình hộp chữ nhật có chiều dài 18 cm, chiều rộng 9 cm và chiều cao 7 cm.

a) Tính diện tích xung quanh của viên gạch.

b) Tính diện tích toàn phần của viên gạch.

Bài 6. Hoàn thành bảng sau:

Hình hộp chữ nhật	Chiều dài	10 dm
	Chiều rộng	8 dm	7 m	8 cm
	Chiều cao	6 dm	5 m
	Chu vi mặt đáy		30 m	40 cm
	Diện tích xung quanh			80 cm2
	Diện tích toàn phần

Bài 7. Tính diện tích kính được sử dụng để làm các bể cá hình hộp chữ nhật có chiều dài 2 m, chiều rộng 1,6 m và chiều cao 1,2 m. Biết bể cá không có nắp.

Bài 8. Một bể bơi dạng hình hộp chữ nhật có chiều dài 12 m, chiều rộng 5 m và chiều sâu 1,8 m. Người ta muốn ốp gạch men xung quanh thành bể bơi. Tính phần diện tích được ốp gách men (diện tích mạch vữa không đáng kể).

Bài 9. Tính diện tích giấy bìa để gấp thành hình hộp chữ nhật có chiều dài 40 cm, chiều rộng 28 cm và chiều cao 34 cm.

Bài 10. Tính diện tích tờ giấy gói quà để gói kín hộp quà hình hộp chữ nhật có chiều dài 24 cm, chiều rộng 19 cm và chiều cao 15 cm.