Giải Toán 10 trang 93 Tập 1 Chân trời sáng tạo

Giải Toán 10 trang 93 Tập 1

Thực hành 5 trang 93 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

a) $\overrightarrow{MA}+\overrightarrow{MD}+\overrightarrow{MB}=\overrightarrow{0}$;

b) $\overrightarrow{ND}+\overrightarrow{NB}+\overrightarrow{NC}=\overrightarrow{0}$;

c) $\overrightarrow{PM}+\overrightarrow{PN}=\overrightarrow{0}$.

Lời giải:

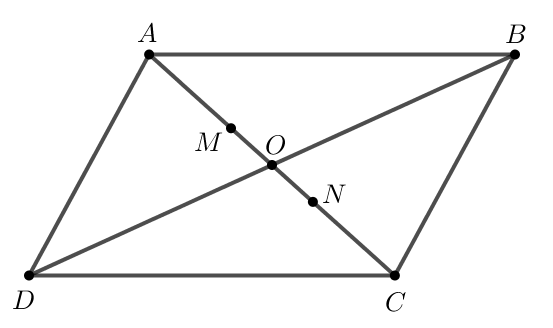
a) Hình bình hành ABCD có tâm O nên O là trung điểm của BD.

Do $\overrightarrow{MA}+\overrightarrow{MD}+\overrightarrow{MB}=\overrightarrow{0}$ nên M là trọng tâm của tam giác ADB.

Khi đó trên AO chọn M sao cho $\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}$.

b) Do $\overrightarrow{N\text{D}}+\overrightarrow{NB}+\overrightarrow{NC}=\overrightarrow{0}$ nên N là trọng tâm của tam giác DBC.

Khi đó trên CO chọn N sao cho $\overrightarrow{CN}=\frac{2}{3}\overrightarrow{CO}$.

c) Do $\overrightarrow{PM}+\overrightarrow{PN}=\overrightarrow{0}$ nên P là trung điểm của MN (1).

Ta có AM = $\frac{2}{3}$AO = $\frac{2}{3}.\frac{1}{2}$AC = $\frac{1}{3}$AC; CN = $\frac{2}{3}$CO = $\frac{2}{3}.\frac{1}{2}$AC = $\frac{1}{3}$AC.

Do đó MN = $\frac{1}{3}$AC.

MO = $\frac{1}{3}$AO = $\frac{1}{3}.\frac{1}{2}$ AC = $\frac{1}{6}$AC.

Khi đó MO = $\frac{1}{2}$MN.

Mà O nằm giữa M và N nên O là trung điểm của MN (2).

Từ (1) và (2) suy ra P trùng O.

Bài tập

Bài 1 trang 93 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và một điểm M tùy ý. Chứng minh rằng:

a) $\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}$;

b) $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$

Lời giải:

a) Do ABCD là hình bình hành nên AB // CD, AB = CD.

Ta thấy hai vectơ $\overrightarrow{BA}$ và $\overrightarrow{DC}$ ngược hướng và $\left|\overrightarrow{BA}\right|=\left|\overrightarrow{DC}\right|$ nên $\overrightarrow{DC}=-\overrightarrow{BA}$.

Do đó $\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{BA}-\overrightarrow{BA}=\overrightarrow{0}$.

b) Do O là giao điểm hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.

Do O là trung điểm của AC nên $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$.

Do O là trung điểm của BD nên $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$.

Ta có $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OC}=2\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OC}=2\overrightarrow{MO}$.

$\overrightarrow{MB}+\overrightarrow{MD}=\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OD}=2\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{OD}=2\overrightarrow{MO}$.

Do đó $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{M\text{D}}$.

Bài 2 trang 93 Toán lớp 10 Tập 1: Cho tứ giác ABCD, thực hiện các phép cộng và trừ vectơ sau:

a) $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}$;

b) $\overrightarrow{AB}-\overrightarrow{AD}$;

c) $\overrightarrow{CB}-\overrightarrow{CD}$.

Lời giải:

a) $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{C\text{D}}+\overrightarrow{DA}$

$$\begin{gathered} =\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\left(\overrightarrow{C\text{D}}+\overrightarrow{DA}\right) \\ =\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{AA}=\overrightarrow{0} \end{gathered}$$

b) $\overrightarrow{AB}-\overrightarrow{A\text{D}}=\overrightarrow{DB}$.

c) $\overrightarrow{CB}-\overrightarrow{C\text{D}}=\overrightarrow{DB}$.

Bài 3 trang 93 Toán lớp 10 Tập 1: Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ:

a) $\overrightarrow{BA}+\overrightarrow{AC}$;

b) $\overrightarrow{AB}+\overrightarrow{AC}$;

c) $\overrightarrow{BA}-\overrightarrow{BC}$.

Lời giải:

a) Ta có $\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{BC}$.

Do đó $\left|\overrightarrow{BA}+\overrightarrow{AC}\right|=\left|\overrightarrow{BC}\right|$ = a.

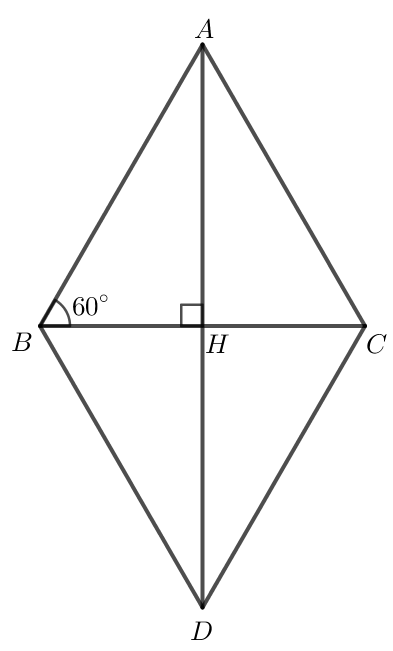
b) Dựng hình bình hành ABDC.

Gọi H là giao điểm của AD và BC.

Áp dụng quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{A\text{D}}$.

Hình bình hành ABDC có AB = AC nên ABDC là hình thoi.

Do đó AD $\perp$ BC tại H.

Do tam giác ABC đều nên $\widehat{ABH}$ = 60^o.

Xét tam giác ABH vuông tại H:

$\sin \widehat{ABH}=\frac{AH}{AB}$

$\Rightarrow$ AH = AB . sin $\widehat{ABH}$ = a . sin 60^o = $\frac{a\sqrt{3}}{2}$.

Do H là giao điểm hai đường chéo của hình thoi ABDC nên H là trung điểm của AD.

Do đó AD = 2AH = 2 . $\frac{a\sqrt{3}}{2}$ = $a\sqrt{3}$.

Vậy $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{A\text{D}}\right|=a\sqrt{3}$.

c) Ta có $\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{CA}$.

Do đó $\left|\overrightarrow{BA}-\overrightarrow{BC}\right|=\left|\overrightarrow{CA}\right|$= a.

Bài 4 trang 93 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng:

a) $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OD}-\overrightarrow{OC}$;

b) $\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{DC}=\overrightarrow{0}$

Lời giải:

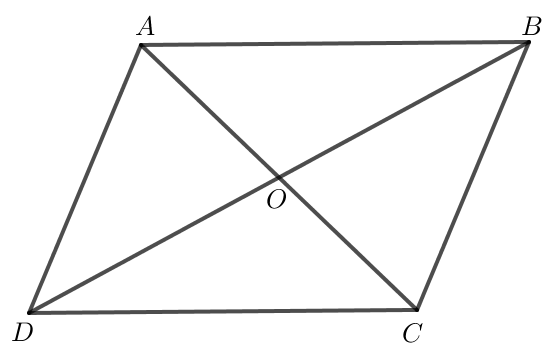
a) Ta có $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$; $\overrightarrow{OD}-\overrightarrow{OC}=\overrightarrow{CD}$.

Do ABCD là hình bình hành nên AB = CD.

Ta thấy hai vectơ $\overrightarrow{BA}$ và $\overrightarrow{CD}$ cùng hướng và $\left|\overrightarrow{BA}\right|=\left|\overrightarrow{\text{CD}}\right|$ nên $\overrightarrow{BA}=\overrightarrow{C\text{D}}$.

Do đó $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OD}-\overrightarrow{OC}$.

b) Ta có $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OD}-\overrightarrow{OC}=\overrightarrow{C\text{D}}$.

Do đó $\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{DC}=\overrightarrow{C\text{D}}+\overrightarrow{DC}=\overrightarrow{CC}=\overrightarrow{0}$.

Vậy $\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{DC}=\overrightarrow{0}$.

Bài 5 trang 93 Toán lớp 10 Tập 1: Cho ba lực  $\overrightarrow{F_1}=\overrightarrow{MA},\overrightarrow{F_2}=\overrightarrow{MB}$ và $\overrightarrow{F_3}=\overrightarrow{MC}$ cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của $\overrightarrow{F_1},\overrightarrow{F_2}$ đều là 10 N và $\widehat{AMB}=90°$. Tìm độ lớn của lực $\overrightarrow{F_3}$.

Lời giải:

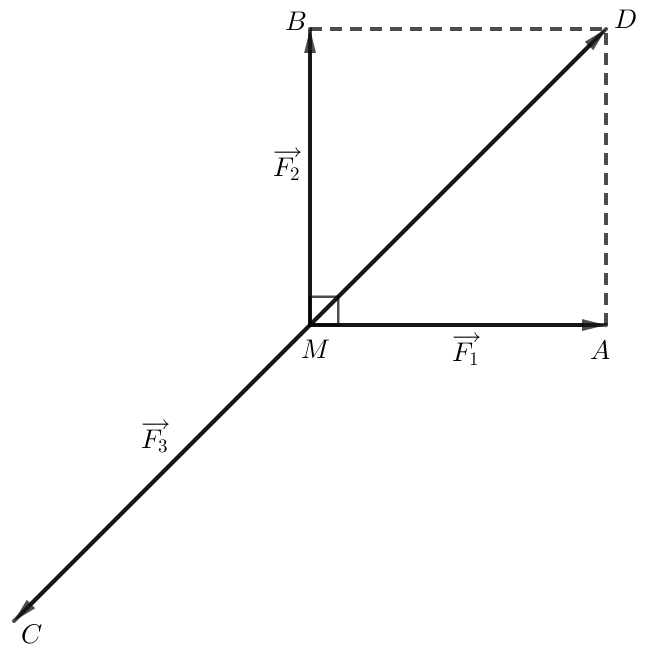
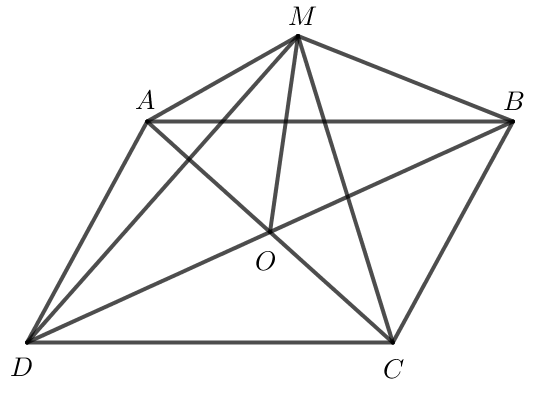
Dựng hình bình hành MBAD.

Do ba lực $\overrightarrow{F_1},\overrightarrow{F_2}$ và $\overrightarrow{F_3}$ cùng tác động vào vật tại điểm M và vật đứng yên nên

$\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{0}$.

Do đó $\overrightarrow{F_3}=-\left(\overrightarrow{F_1}+\overrightarrow{F_2}\right)$.

Áp dụng quy tắc hình bình hành ta có:

$\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MD}$ hay $\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{MD}$.

Do đó $\overrightarrow{F_3}=-\overrightarrow{M\text{D}}$.

Hình bình hành MBAD có $\widehat{AMB}$ = 90^o và MA = MB nên MBAD là hình vuông.

Áp dụng định lí Pythagore vào tam giác MAD vuông tại A có:

MD² = MA² + AD²

$\Rightarrow$ MD² = 10² + 10²

$\Rightarrow$ MD² = 2.10²

$\Rightarrow$ MD = $10\sqrt{2}$ N (do MD là độ dài đoạn thẳng nên MD > 0).

$\Rightarrow \left|\overrightarrow{F_3}\right|=\left|-\overrightarrow{M\text{D}}\right|=10\sqrt{2}$ N.

Vậy cường độ của lực $\overrightarrow{F_3}$ là $10\sqrt{2}$ N.

Bài 6 trang 93 Toán lớp 10 Tập 1: Khi máy bay nghiêng cánh một góc α, lực $\overrightarrow{F}$ của không khí tác động vuông góc với cánh và bằng tổng của lực nâng $\overrightarrow{F_1}$ và lực cản $\overrightarrow{F_2}$ (Hình 16). Cho biết α = 30° và $\left|\overrightarrow{F}\right|=a$. Tính $\left|\overrightarrow{F_1}\right|$ và $\left|\overrightarrow{F_2}\right|$ theo a.

Lời giải:

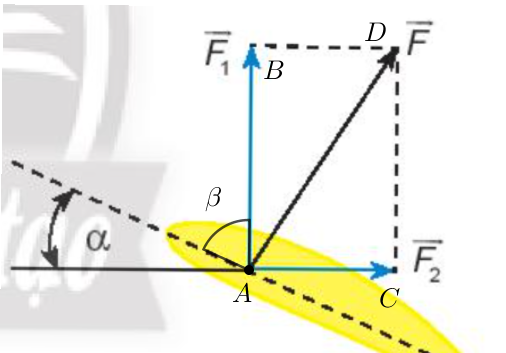
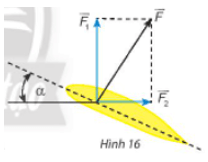
Đặt tên các điểm đầu và điểm cuối của các vectơ và tên góc như trên hình.

Khi đó ABDC là hình chữ nhật.

Ta có $\widehat{BA\text{D}}$ = α (cùng phụ với β).

Do đó $\widehat{BA\text{D}}$ = 30^o.

Tam giác ABD vuông tại B nên $\cos \widehat{BAD}=\frac{BA}{AD}$

$\Rightarrow$ BA = AD . cos $\widehat{BA\text{D}}$ = a . cos 30^o = $\frac{a\sqrt{3}}{2}$.

$\sin \widehat{BAD}=\frac{BD}{AD}\Rightarrow$BD = AD. sin $\widehat{BAD}$ = a . sin 30^o = $\frac{a}{2}$.

Do ABDC là hình chữ nhật nên BD = AC = $\frac{a}{2}$.

Vậy $\left|\overrightarrow{F_1}\right|=\frac{a\sqrt{3}}{2};\left|\overrightarrow{F_2}\right|=\frac{a}{2}$.

Bài 7 trang 93 Toán lớp 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: $\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{0};\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$; $\overrightarrow{HA}+\overrightarrow{HD}+\overrightarrow{HC}=\overrightarrow{0}$. Tính độ dài các vectơ $\overrightarrow{KA},\overrightarrow{GH},\overrightarrow{AG}$.

Lời giải:

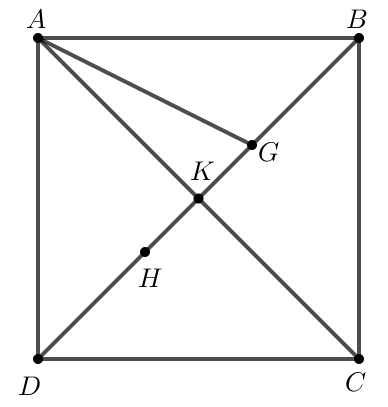
Do $\overrightarrow{K\text{A}}+\overrightarrow{KC}=\overrightarrow{0}$ nên K là trung điểm của AC.

Do đó K là giao điểm hai đường chéo của hình vuông ABCD.

Do $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ nên G là trọng tâm của tam giác ABC.

Khi đó trên đoạn BK chọn điểm G sao cho $\overrightarrow{BG}=\frac{2}{3}\overrightarrow{BK}$.

Do $\overrightarrow{HA}+\overrightarrow{H\text{D}}+\overrightarrow{HC}=\overrightarrow{0}$ nên H là trọng tâm của tam giác ADC.

Khi đó trên đoạn DK chọn điểm H sao cho $\overrightarrow{DH}=\frac{2}{3}\overrightarrow{DK}$.

Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:

AC² = AD² + DC²

$\Rightarrow$ AC² = a² + a²

$\Rightarrow$ AC² = 2a²

$\Rightarrow$ AC = $\sqrt{2}$a (do AC là độ dài đoạn thẳng nên AC > 0)

Do K là trung điểm của AC nên AK = $\frac{1}{2}$AC = $\frac{\sqrt{2}a}{2}$.

Do đó $\left|\overrightarrow{K\text{A}}\right|=\frac{\sqrt{2}a}{2}$.

Do ABCD là hình vuông nên AC = BD.

Do đó BD = $\sqrt{2}$a.

Do H là trọng tâm của tam giác ADC nên HK = $\frac{1}{3}$DK = $\frac{1}{3}.\frac{1}{2}$BD = $\frac{1}{6}$BD = $\frac{\sqrt{2}a}{6}$.

Do G là trọng tâm của tam giác ABC nên KG = $\frac{1}{3}$BK = $\frac{1}{3}.\frac{1}{2}$BD = $\frac{1}{6}$BD = $\frac{\sqrt{2}a}{6}$.

Do đó HK + KG = $\frac{\sqrt{2}a}{6}$+ $\frac{\sqrt{2}a}{6}$ hay HG = $\frac{\sqrt{2}a}{3}$.

Do đó $\left|\overrightarrow{GH}\right|=\frac{\sqrt{2}a}{3}$.

Do ABCD là hình vuông là K là giao điểm hai đường chéo nên AC $\perp$ BD tại K.

Áp dụng định lí Pythagore vào tam giác AKG vuông tại K có:

AG² = AK² + KG²

$\Rightarrow$ AG² = ${\left(\frac{\sqrt{2}a}{2}\right)}^2+{\left(\frac{\sqrt{2}a}{6}\right)}^2$

$\Rightarrow$ AG² = $\frac{5{\text{a}}^2}{9}$

$\Rightarrow$ AG = $\frac{\sqrt{5}a}{3}$ (do AG là độ dài đoạn thẳng nên AG > 0)

Do đó $\left|\overrightarrow{AG}\right|=\frac{\sqrt{5}a}{3}$.

Vậy $\left|\overrightarrow{K\text{A}}\right|=\frac{\sqrt{2}a}{2}$; $\left|\overrightarrow{GH}\right|=\frac{\sqrt{2}a}{3}$; $\left|\overrightarrow{AG}\right|=\frac{\sqrt{5}a}{3}$.

Bài 8 trang 93 Toán lớp 10 Tập 1: Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước là một vectơ theo hướng đông như Hình 17. Tính độ dài vectơ tổng của hai vectơ mói trên.

Lời giải:

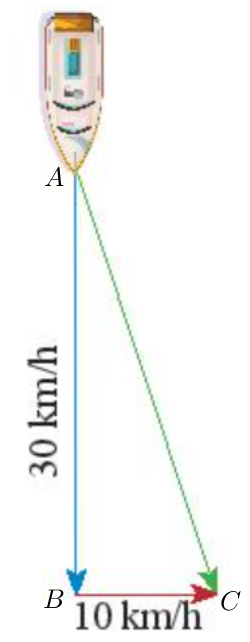
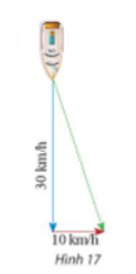
Đặt tên điểm đầu và điểm cuối của các vectơ như hình trên.

Khi đó vectơ vận tốc của con tàu là vectơ $\overrightarrow{AB}$; vectơ vận tốc của dòng nước là vectơ $\overrightarrow{BC}$.

Khi đó vectơ tổng của hai vectơ trên là $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B:

AC² = AB² + BC²

$\Rightarrow$ AC² = 30² + 10²

$\Rightarrow$ AC² = 1 000

$\Rightarrow$ AC = $10\sqrt{10}$ (do AC là độ dài đoạn thẳng nên AC > 0)

Vậy độ dài tổng của hai vectơ trên là $10\sqrt{10}$ km/h.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 10 trang 88 Tập 1

Giải Toán 10 trang 89 Tập 1

Giải Toán 10 trang 90 Tập 1

Giải Toán 10 trang 91 Tập 1

Giải Toán 10 trang 92 Tập 1

Giải Toán 10 trang 93 Tập 1

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ