Giải Toán 10 trang 74 Tập 2 Chân trời sáng tạo

Giải Toán 10 trang 74 Tập 2

Bài tập 4 trang 74 Toán lớp 10 Tập 2: Tính bán kính của đường tròn tâm M(−2; 3) và tiếp xúc với đường thẳng d: 14x − 5y + 60 = 0.

Lời giải:

Vì đường tròn tâm M tiếp xúc với đường thẳng d: 14x − 5y + 60 = 0 nên R = d(M; d)

Ta có: d(M; d) = $\frac{\left|14.(-2)-5.3+60\right|}{\sqrt{{14}^2+{(-5)}^2}}$  = $\frac{\sqrt{221}}{13}$ .

⇒ R = d(M; d) = $\frac{\sqrt{221}}{13}$

Vậy bán kính của đường tròn tâm M(−2; 3) và tiếp xúc với đường thẳng d: 14x − 5y + 60 = 0 là $\frac{\sqrt{221}}{13}$ .

Bài tập 5 trang 74 Toán lớp 10 Tập 2: Tính khoảng cách giữa hai đường thẳng: Δ: 6x + 8y – 13 = 0 và Δ′: 3x + 4y – 27 = 0.

Lời giải:

Ta có Δ: 6x + 8y – 13 = 0 và Δ′: 3x + 4y – 27 = 0 có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}$  =(6 ; 8) và $\overrightarrow{n_2}$  = (3 ; 4).

Khi đó:   ⇒ Δ và Δ′ song song hoặc trùng nhau.

Lấy điểm $A\left(0;\frac{13}{8}\right)$  ∈ Δ.

Thay tọa độ điểm M vào phương trình Δ′ ta được : 3.0 + 4. $\frac{13}{8}$ – 27 = $-\frac{41}{2}$  ≠ 0.

Suy ra Δ // Δ′.

Khi đó d(Δ, Δ′) = d(A; Δ′) = $\frac{\left|3.0+4.\frac{13}{8}-27\right|}{\sqrt{3^2+4^2}}$  = $\frac{41}{10}$  = 4,1.

Vậy khoảng cách giữa hai đường thẳng: Δ: 6x + 8y – 13 = 0 và Δ′: 3x + 4y – 27 = 0 là 4,1.

Bài tập 6 trang 74 Toán lớp 10 Tập 2: Tìm tâm và bán kính của các đường tròn có phương trình:

a) (x − 2)² + (y − 7)² = 64;

b) (x + 3)² + (y + 2)² = 8;

c) x² + y² − 4x − 6y – 12 = 0.

Lời giải:

a) Phương trình đường tròn (x − 2)² + (y − 7)² = 64 có dạng (x − a)² + (y − b)² = R².

⇒ Đường tròn có tâm I(2; 7) và bán kính R = 8.

Vậy đường tròn (x − 2)² + (y − 7)² = 64 có tâm I(2; 7) và bán kính R = 8.

b) Phương trình đường tròn (x + 3)² + (y + 2)² = 8 có dạng (x − a)² + (y − b)² = R².

⇒ Đường tròn có tâm I(−3; −2) và bán kính R = $2\sqrt{2}$ .

Vậy đường tròn (x + 3)² + (y + 2)² = 8 có tâm I(−3; −2) và bán kính R = $2\sqrt{2}$ .

c) Phương trình x² + y² − 4x − 6y – 12 = 0 có dạng x² + y² − 2ax − 2by + c = 0 với a = 2, b = 3, c = −12

Ta có: a² + b² − c = 2² + 3² + 12 = 25 ⇒ bán kính R = $\sqrt{a^2+b^2-c }=\sqrt{25}$  = 5.

Vậy đường tròn x² + y² − 4x − 6y – 12 = 0 có tâm I(2; 3) và bán kính R = 5.

Bài tập 7 trang 74 Toán lớp 10 Tập 2: Lập phương trình đường tròn trong các trường hợp sau:

a) Có tâm I(−2; 4) và bán kính bằng 9;

b) Có tâm I(1; 2) và đi qua điểm A(4; 5);

c) Đi qua hai điểm A(4; 1), B(6; 5) và có tâm nằm trên đường thẳng 4x + y – 16 = 0;

d) Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là a, tung độ là b.

Lời giải:

a) Phương trình đường tròn có tâm I(−2; 4) và bán kính R = 9 là: (x + 2)² + (y − 4)² = 81.

b) Ta có

Vì đường tròn đi qua điểm A nên  ta có: R = IA = $3\sqrt{2}$

Vậy phương trình đường tròn có tâm I(1; 2) và bán kính R = $3\sqrt{2}$ là: (x − 1)² + (y − 2)² = 18.

c) Phương trình đường tròn tâm I(a; b) có dạng: x² + y² − 2ax − 2by + c = 0.

Vì I(a; b) thuộc đường thẳng 4x + y − 16 = 0 và các điểm A(4; 1), B(6; 5) thuộc đường tròn nên ta có hệ phương trình sau:

$\left\{\begin{array}{l}4a+b-16=0\\ 4^2+1^2-8a-2b+c=0\\ 6^2+5^2-12a-10b+c=0\end{array}\right.$ ⇔ $\left\{\begin{array}{l}4a+b-16=0\\ -8a-2b+c=-17\\ -12a-10b+c=-61\end{array}\right.$  ⇔ $\left\{\begin{array}{l}a=3\\ b=4\\ c=15\end{array}\right.$

Vậy phương trình đường tròn là: x² + y² − 6x − 8y + 15 = 0.

d) Phương trình đường tròn (C) tâm I(m; n) có dạng: x² + y² – 2mx – 2ny + c = 0.

Vì O(0; 0) ∈ (C) nên thay tọa độ O(0; 0) vào (C) ta được c = 0

Vì (C) cắt trục hoành tại điểm có tọa độ (a; 0) và cắt trục tung tại điểm có tọa độ (0; b) nên ta có: $\left\{\begin{array}{l}{a}^2-2ma=0\\ b^2-2nba=0\end{array}\right.$ ⇔ $\left\{\begin{array}{l}m=\frac{a}{2}\\ n=\frac{b}{2}\end{array}\right.$  (vì a ≠ 0, b ≠ 0).

Vậy phương trình đường tròn (C) là: x² + y² – ax – by = 0.

Bài tập 8 trang 74 Toán lớp 10 Tập 2: Viết phương trình tiếp tuyến của đường tròn (C): (x − 5)² + (y − 3)² = 100 tại điểm M(11; 11).

Lời giải:

Đường tròn (C): (x − 5)² + (y − 3)² = 100 có tâm I(5; 3).

Khi đó phương trình tiếp tuyến của đường tròn (C) tại M(11; 11) là:

(5 − 11)(x − 11) + (3 − 11)(y − 11) = 0

⇔ −6x − 8y + 154 = 0

⇔ 3x + 4y – 77 = 0.

Vậy phương trình tiếp tuyến của đường tròn (C): (x − 5)² + (y − 3)² = 100 tại điểm M(11; 11) là : 3x + 4y – 77 = 0.

Bài tập 9 trang 74 Toán lớp 10 Tập 2: Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:

a) $\frac{x^2}{100}+\frac{y^2}{36}=1$ ;

b) $\frac{x^2}{25}+\frac{y^2}{16}=1$ ;

c)  x² + 16y² = 16.

Lời giải:

a) Với (E): $\frac{x^2}{100}+\frac{y^2}{36}=1$

Phương trình elip (E) có dạng: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

⇒ a = 10; b = 6 ⇒ c =  $\sqrt{a^2-b^2}$ = $\sqrt{{10}^2-6^2}$  = 8.

Vậy tọa độ các tiêu điểm là: (−8; 0) và (8; 0).

Tọa độ các đỉnh là: (−10; 0), (10; 0), (0; −6); (0; 6).

Độ dài trục lớn bằng 2a = 2. 10 = 20; độ dài trục nhỏ bằng 2b = 2.6 = 12.

b) Với (E): $\frac{x^2}{25}+\frac{y^2}{16}=1$

Phương trình elip (E) có dạng: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

⇒ a = 5; b = 4 ⇒ c = $\sqrt{a^2-b^2}$ = $\sqrt{5^2-4^2}$  = 3.

Vậy tọa độ các tiêu điểm là: (−3; 0) và (3; 0).

Tọa độ các đỉnh là: (−5; 0), (5; 0), (0; −4); (0; 4)

Độ dài trục lớn bằng 2a = 2. 5 = 10; độ dài trục nhỏ bằng 2b = 2. 4 = 8.

c) Ta có: x² + 16y² = 16 ⇔ $\frac{x^2}{16}+\frac{y^2}{1^2}=1$ .

Phương trình elip (E) có dạng: 

⇒ a = 4; b = 1 ⇒ c = $\sqrt{a^2-b^2}$ = $\sqrt{4^2-1^2}$  = $\sqrt{15}$ .

Vậy tọa độ các tiêu điểm là: $\left(-\sqrt{15};0\right)$  và $\left(\sqrt{15};0\right)$ .

Tọa độ các đỉnh là: (−4; 0), (4; 0), (0; −1); (0; 1).

Độ dài trục lớn bằng 2a = 2. 4 = 8; độ dài trục nhỏ bằng 2b = 2. 1 = 2.

Bài tập 10 trang 74 Toán lớp 10 Tập 2: Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:

a) Đỉnh (5; 0), (0; 4);

b) Đỉnh (5; 0), tiêu điểm (3; 0);

c) Độ dài trục lớn 16, độ dài trục nhỏ 12;

d) Độ dài trục lớn 20, tiêu cự 12.

Lời giải:

a) Elip có đỉnh (5; 0), (0; 4) ⇒ a = 5; b = 4.

⇒ Phương trình elip (E) là: $\frac{x^2}{25}+\frac{y^2}{16}=1$ .

Vậy elip thỏa mãn điều kiện đỉnh (5; 0), (0; 4) là $\frac{x^2}{25}+\frac{y^2}{16}=1$ .

b) Elip có đỉnh (5; 0) ⇒ a = 5; tiêu điểm (3; 0) ⇒ c = 3

⇒ b = $\sqrt{a^2-c^2}$  = $\sqrt{5^2-3^2}$  = 4

Vậy phương trình elip cần tìm là: $\frac{x^2}{25}+\frac{y^2}{16}=1$ .

c) Vì độ dài trục lớn 16, độ dài trục nhỏ 12 nên ta có: 2a = 16; 2b = 12 

⇒ a = 8; b = 6

⇒ Phương trình elip (E) là: $\frac{x^2}{64}+\frac{y^2}{36}=1$ .

Vậy phương trình elip cần tìm là: $\frac{x^2}{64}+\frac{y^2}{36}=1$ .

d) Vì độ dài trục lớn 20, tiêu cự 12 nên ta có: 2a = 20; 2c = 12 

⇒ a = 10; c = 6 

⇒ b = $\sqrt{a^2-c^2}$  = $\sqrt{{10}^2-6^2}$  = 8.

⇒ Phương trình elip (E) là: $\frac{x^2}{100}+\frac{y^2}{64}=1$ .

Vậy phương trình elip cần tìm là: $\frac{x^2}{100}+\frac{y^2}{64}=1$ .

Bài tập 11 trang 74 Toán lớp 10 Tập 2: Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:

a)  $\frac{x^2}{16}-\frac{y^2}{9}=1$;

b) $\frac{x^2}{64}-\frac{y^2}{36}=1$ ;

c) x² − 16y² =16;

d) 9x² − 16y² = 144.

Lời giải:

a) Với hypebol (H): $\frac{x^2}{16}-\frac{y^2}{9}=1$

Phương trình hypebol (H) có dạng: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

⇒ a = 4; b = 3 ⇒ c =  $\sqrt{a^2+b^2}$ = $\sqrt{4^2+3^2}$  = 5.

Vậy tọa độ các tiêu điểm là (−5; 0), (5; 0).

Tọa độ các đỉnh là (−4; 0), (4; 0).

Độ dài trục thực là: 2a = 2. 4 = 8; độ dài trục ảo là: 2b = 2. 3 = 6.

b) Với hypebol (H): $\frac{x^2}{64}-\frac{y^2}{36}=1$

Phương trình hypebol (H) có dạng: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

⇒ a = 8; b = 6 ⇒ c = $\sqrt{a^2+b^2}$ = $\sqrt{8^2+6^2}$  = 10.

Vậy tọa độ các tiêu điểm là (−10; 0), (10; 0)

Tọa độ các đỉnh là (−8; 0), (8; 0)

Độ dài trục thực là: 2a = 2. 8 = 16; độ dài trục ảo là: 2b = 2. 6 = 12.

c) Ta có: x² − 16y² =16 ⇔ $\frac{x^2}{16}-\frac{y^2}{1^2}=1$

⇒ a = 4; b = 1 ⇒ c = $\sqrt{a^2+b^2}$  = $\sqrt{4^2+1^2}$  = $\sqrt{17}$ .

Vậy tọa độ các tiêu điểm là $\left(-\sqrt{17};0\right)$  , $\left(\sqrt{17};0\right)$

Tọa độ các đỉnh là (−4; 0), (4; 0)

Độ dài trục thực là: 2a = 2. 4 = 8; độ dài trục ảo là: 2b = 2. 1 = 2.

d) Ta có: 9x² − 16y² = 144 ⇔   $\frac{x^2}{16}-\frac{y^2}{9}=1$

⇒ a = 4; b = 3 ⇒ c = $\sqrt{a^2+b^2}$  = $\sqrt{4^2+3^2}$  =5.

Vậy tọa độ các tiêu điểm là (−5; 0), (5; 0)

Tọa độ các đỉnh là (−4; 0), (4; 0).

 Độ dài trục thực là: 2a = 2. 4 = 8; độ dài trục ảo là: 2b = 2. 3 = 6.

Bài tập 12 trang 74 Toán lớp 10 Tập 2: Viết phương trình chính tắc của hypebol thỏa mãn từng điều kiện sau:

a) Đỉnh (3; 0), tiêu điểm (5; 0);

b) Độ dài trục thực 8, độ dài trục ảo 6.

Lời giải:

a) Gọi phương trình chính tắc của hypebol (H) là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ .

Hypebol có đỉnh (3; 0) ⇒ a = 3; tiêu điểm (5; 0) ⇒  c = 5.

⇒ b =  $\sqrt{c^2-a^2}$ =$\sqrt{5^2-3^2}$  = 4.

Thay a = 3 và b = 4 vào phương trình $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ , ta được:

$\frac{x^2}{3^2}-\frac{y^2}{4^2}=1$ ⇔ $\frac{x^2}{9}-\frac{y^2}{16}=1$ .

Vậy phương trình chính tắc của hypebol (H) là: $\frac{x^2}{9}-\frac{y^2}{16}=1$

b)  Gọi phương trình chính tắc của hypebol (H) là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Hypebol có độ dài trục thực 8, độ dài trục ảo 6 nên 2a = 8; 2b = 6 

⇒ a = 4; b = 3.

Thay a = 4 và b = 3 vào phương trình $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ , ta được:

$\frac{x^2}{4^2}-\frac{y^2}{3^2}=1$ ⇔ $\frac{x^2}{16}-\frac{y^2}{9}=1$ .

Vậy phương trình hypebol là:  $\frac{x^2}{16}-\frac{y^2}{9}=1$.

Bài tập 13 trang 74 Toán lớp 10 Tập 2: Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:

a) y² = 12x;                       

b) y² = x.

Lời giải:

a) Với parabol y² = 12x :                       

Phương trình parabol có dạng: y² = 2px ⇒ 2p = 12 ⇒ p = 6 ⇒ $\frac{p}{2}$  = 3.

Vậy tọa độ tiêu điểm là (3; 0) và phương trình đường chuẩn là  x + 3 = 0.

b) Với parabol y² = x:

Phương trình parabol có dạng: y² = 2px ⇒ 2p = 1 ⇒ p = $\frac{1}{2}$  ⇒ $\frac{p}{2}$  = $\frac{1}{4}$ .

Vậy tọa độ tiêu điểm là $\left(\frac{1}{4};0\right)$  và phương trình đường chuẩn là x + $\frac{1}{4}$  = 0.

Bài tập 14 trang 74 Toán lớp 10 Tập 2: Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau:

a) Tiêu điểm (4; 0);

b) Đường chuẩn có phương trình x = $-\frac{1}{6}$ ;

c) Đi qua điểm (1; 4);

d) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 8.

Lời giải:

a) Parabol (P) có tiêu điểm (4; 0) ⇒ $\frac{p}{2}$  = 4 ⇒ p = 8.

⇒ Phương trình parabol (P) là: y² = 2.8x = 16x.

Vậy phương trình parabol (P) là: y² = 16x.

b. Parabol (P) có đường chuẩn là  x = $-\frac{1}{6}$ ⇒ p = $\frac{1}{3}$

⇒ Phương trình parabol (P) là: y² = 2. $\frac{1}{3}$ x = $\frac{2}{3}$ x.

Vậy phương trình parabol (P) là: y² = $\frac{2}{3}$ x.

c)  Parabol (P) đi qua điểm (1; 4) nên thay tọa độ (1; 4) vào phương trình : y² = 2px, ta được: 4²  = 2p. 1 ⇒ p = 8.

⇒ Phương trình parabol (P) là: y² = 2.8x = 16x.

Vậy phương trình parabol (P) là: y² = 16x.

d) Parabol (P) tiêu điểm $F\left(\frac{p}{2};0\right)$ , phương trình đường chuẩn ∆ : x + $\frac{p}{2}$  = 0.

Vì parabol (P) có khoảng cách từ tiêu điểm đến đường chuẩn bằng 8 nên:

d(F, Δ) = 8 ⇔ $\frac{\left|\frac{p}{2}+\frac{p}{2}\right|}{\sqrt{1^2+0^2}}$  = 8 ⇔ p = 8.

⇒ Phương trình parabol (P) là: y² = 2.8x = 16x.

Vậy phương trình parabol (P) là: y² = 16x.

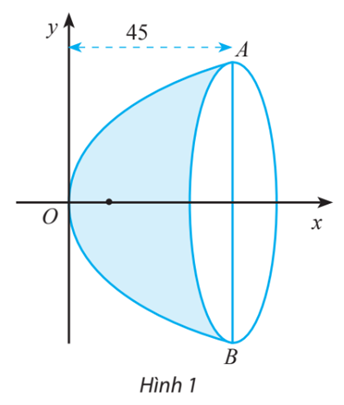
Bài tập 15 trang 74 Toán lớp 10 Tập 2:  Một gương lõm có mặt cắt hình parabol như Hình 1, có tiêu điểm cách đỉnh 5 cm. Cho biết bề sâu của gương là 45 cm, tính khoảng cách AB.

Lời giải:

Vì parabol (P) có tiêu điểm cách đỉnh 5 cm ⇒ Tiêu điểm có tọa độ (5; 0) ⇒ p = 10

⇒ Phương trình parabol (P): y² = 20x.

Ta có điểm A(45; y_A) ∈ (P) nên thay tọa độ A vào phương trình (P), ta được:

y_A² = 20. 45 ⇒ y_A = 30

⇒ AB = 2. 30 = 60 (cm).

Vậy khoảng cách AB là 60cm.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

Giải Toán 10 trang 73 Tập 2

Giải Toán 10 trang 74 Tập 2

Giải Toán 10 trang 75 Tập 2

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Bài tập cuối chương 10

Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra

Bài 2: Vẽ ba đường conic bằng phần mềm Geogebra