Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 75 Tập 2 Chân trời sáng tạo

    Với giải bài tập Toán lớp 10 trang 75 Tập 2 trong Bài tập cuối chương 9 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 75 Tập 2.

    1 1,033 24/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 75 Tập 2

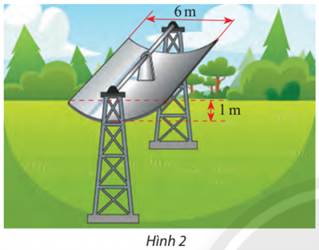
    Bài tập 16 trang 75 Toán lớp 10 Tập 2: Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (Hình 2). Nước sẽ chảy thông qua một dường ống nằm ở tiêu điểm của parabol.

    a) Viết phương trình chính tắc của parabol.

    b) Tính khoảng cách từ tâm đường ống đến đỉnh của parabol.

    Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 9 (ảnh 1)

    Lời giải:

    a) Chọn hệ tọa độ như hình vẽ:

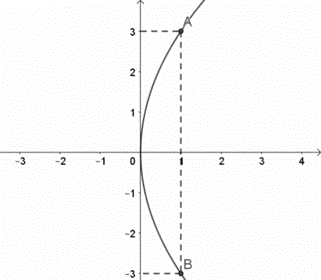
    Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 9 (ảnh 1)

    Phương trình parabol (P) có dạng: y2 = 2px.

    Ta có: A(1; 3) ∈ (P) nên thay tọa độ điểm A vào phương trình (P), ta được:

    32 = 2p. 1 ⇒ p = 92 .

    Vậy phương trình chính tắc của parabol (P) là: y2 = 9x.

    b) Vì đường ống nằm ở tiêu điểm của (P) nên khoảng cách từ tâm đường ống đến đỉnh của parabol bằng: p2  = 2,25 (m).

    Vậy khoảng cách từ tâm đường ống đến đỉnh của parabol khoảng 2,25 mét.

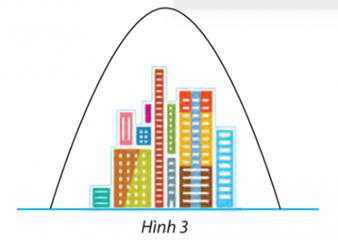
    Bài tập 17 trang 75 Toán lớp 10 Tập 2: Cổng chào của một thành phố có dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (Hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc vẽ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng.

    Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 9 (ảnh 1)

    Lời giải:

    Chọn hệ tọa độ như hình vẽ:

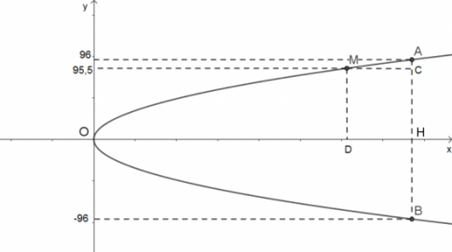
    Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 9 (ảnh 1)

    Gọi phương trình parabol là y2 = 2px.

    Gọi chiều cao của cổng là OH = h.

    Khoảng cách giữa hai chân cổng là AB = 192 ⇒ AH = 96 ⇒ Điểm A có tọa độ (h; 96).

    Ta có: AC = 0,5; DH = MC = 2 ⇒ Điểm M có tọa độ (h − 2; 95,5).

    Vì A và M thuộc parabol (P) nên ta có hệ phương trình:

    962=2ph95,52=2p(h−2) ⇒ 96295,52=hh−2  ⇒ h = 2.962962−95,52  ≈ 192,5 (m)

    Vậy chiều cao của cổng khoảng 192,5 m.

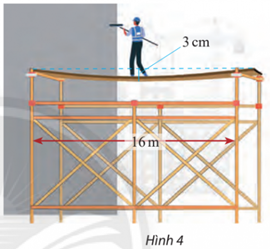
    Bài tập 18 trang 75 Toán lớp 10 Tập 2: Một người đứng ở giữa một tấm ván gỗ đặt trên một giàn giáo để sơn tường nhà. Biết rằng giàn giáo dài 16 m và độ võng tại tâm của ván gỗ (điểm ở giữa ván gỗ) là 3 cm (Hình 4). Cho biết đường cong của ván gỗ có hình parabol.

    a) Giả sử tấm ván gỗ trùng với đỉnh của parabol, tìm phương trình chính tắc của parabol.

    b) Điểm có độ võng 1 cm cách tâm ván gỗ bao xa?

    Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 9 (ảnh 1)

    Lời giải:

    a) Chọn hệ tọa độ như hình vẽ sau:

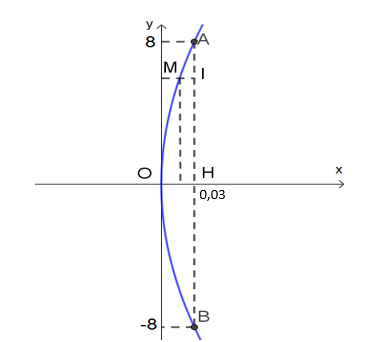
    Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 9 (ảnh 1)

    Gọi phương trình của parabol (P) có dạng: y2 = 2px.

    Ta có giàn giáo dài 16 m và độ võng tại tâm của ván gỗ (điểm ở giữa ván gỗ) là 3cm = 0,03m, nên AB = 16, OH = 0,03 ⇒ điểm A có tọa độ (0,03; 8).

    Vì A thuộc (P) nên thay tọa độ điểm A vào phương trình (P), ta được:

    82  = 2p. 0,03 ⇒ p = 822.0,03  = 32003 .

    ⇒ Phương trình chính tắc của parabol (P) là: y2 = 2. 32003 x = 64003 x.

    Vậy phương trình chính tắc của parabol (P) là: y2 = 64003 x.

    b) Tại điểm có độ võng 1 cm = 0,01 m. Khi đó MI = 0,01 ⇒ M(0,02; yM)

    Vì M ∈ (P) nên thay tọa độ điểm M vào phương trình (P), ta được: 

    yM2 = 64003 . 0,02 ⇒ yM =  863.

    ⇒  M0,02;863 ⇒ OM = OM→  = (0,02−0)2+863−02  ≈ 6,53.

    Vậy điểm M có độ võng 1 cm cách tâm ván gỗ khoảng 6,53 mét.

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

    Giải Toán 10 trang 73 Tập 2

    Giải Toán 10 trang 74 Tập 2

    Giải Toán 10 trang 75 Tập 2

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 1: Không gian mẫu và biến cố

    Bài 2: Xác suất của biến cố

    Bài tập cuối chương 10

    Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra

    Bài 2: Vẽ ba đường conic bằng phần mềm Geogebra

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,033 24/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: