Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 102 Tập 1 Chân trời sáng tạo

    Với giải bài tập Toán lớp 10 trang 102 Tập 1 trong Bài tập cuối chương 5 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 102 Tập 1.

    1 191 22/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 102 Tập 1

    Bài 1 trang 102 Toán lớp 10 Tập 1: Cho ba vectơ a→,   b→,   c→ đều khác vectơ 0→. Các khẳng định sau đúng hay sai?

    a) Nếu hai vectơ a→,   b→ cùng phương với c→ thì a→ và b→ cùng phương.

    b) Nếu hai vectơ a→,   b→ cùng ngược hướng với c→ thì a→ và b→ cùng hướng.

    Lời giải:

    a) Hai vectơ a→ và c→ cùng phương nên a→=k1.c→ (k1 ≠ 0).

    Hai vectơ b→ và c→ cùng phương nên b→=k2.c→ (k2 ≠ 0).

    Khi đó a→b→=k1.c→k2.c→=k1k2⇒a→=k1k2.b→.

    Do đó hai vectơ a→ và b→ cùng phương.

    Vậy khẳng định a đúng.

    b) Hai vectơ a→ và c→ ngược hướng nên a→=−k1.c→ (k1 > 0).

    Hai vectơ b→ và c→ ngược hướng nên b→=−k2.c→ (k2 > 0).

    Khi đó a→b→=−k1.c→−k2.c→=k1k2⇒a→=k1k2.b→ với k1k2>0.

    Do đó hai vectơ a→ và b→ cùng hướng.

    Vậy khẳng định b đúng.

    Bài 2 trang 102 Toán lớp 10 Tập 1: Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.

    a) Tính độ dài của các vectơ AC→,  BD→.

    b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng a102.

    Lời giải:

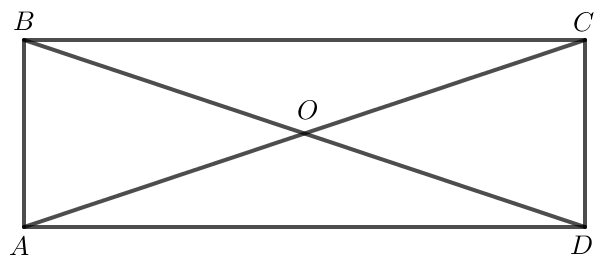
    Giải Toán 10 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

    a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại B:

    AC2 = AB2 + BC2

    ⇒ AC2 = a2 + (3a)2

    ⇒ AC2 = 10a2

    ⇒ AC = 10a (do AC là độ dài đoạn thẳng nên AC > 0)

    Do ABCD là hình chữ nhật nên AC = BD = 10a.

    Vậy AC→=BD→=10a.

    b) Ta thấy a102 = 12.10a.

    Do đó độ dài các vectơ đó bằng 12 độ dài của AC và BD.

    Vậy các cặp vectơ đối nhau và có độ dài bằng a102 là: OB→ và OD→; OA→ và OC→; BO→ và DO→; AO→ và CO→.

    Bài 3 trang 102 Toán lớp 10 Tập 1: Cho hình thoi ABCD có cạnh bằng a và có góc A bằng 60°. Tìm độ dài các vectơ sau: p→=AB→+AD→ ; u→=AB→−AD→ ; v→=2AB→−AC→.

    Lời giải:

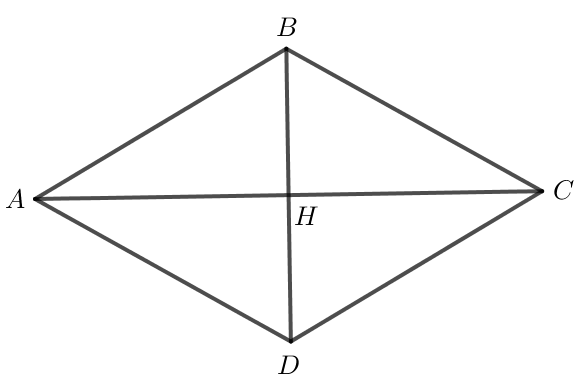
    Giải Toán 10 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

    +) Tính p→:

    Áp dụng quy tắc hình bình hành ta có AB→+AD→=AC→.

    Do đó p→=AB→+AD→=AC→.

    Hình thoi ABCD có hai đường chéo AC và BD nên AC là tia phân giác của BAD^.

    Do đó BAC^=30°.

    Tam giác ABC cân tại B nên BAC^=BCA^=30°.

    Khi đó ABC^=180°−2.30°=120°.

    Áp dụng định lí côsin vào tam giác ABC ta có:

    AC2 = AB2 + BC2 - 2.AB.BC.cos ABC^

    ⇒ AC2 = a2 + a2 - 2.a.a.cos 120o

    ⇒ AC2 = 2a2 + a2

    ⇒ AC2 = 3a2

    ⇒ AC = 3a (do AC là độ dài đoạn thẳng nên AC > 0)

    Do đó p→=3a.

    +) Tính u→:

    Ta có u→=AB→−AD→=DB→.

    Do đó u→=DB→.

    Tam giác ABD cân tại A có BAD^=60° nên tam giác ABD đều.

    Do đó BD = AB = a.

    Do đó u→=DB→ = a.

    +) Tính v→:

    Gọi H là giao điểm của AC và BD.

    H là giao điểm hai đường chéo của hình thoi ABCD nên AC→=2AH→.

    Do đó 2AB→−AC→=2AB→−2AH→=2AB→−AH→=2HB→.

    Khi đó 2AB→−AC→=2HB→=DB→=a.

    Do đó v→=a.

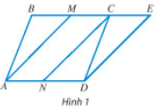
    Bài 4 trang 102 Toán lớp 10 Tập 1: Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho CE→=AN→ (Hình 1).

    Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC

    a) Tìm tổng của các vectơ NC→ và MC→; AM→ và CD→; AD→ và NC→.

    b) Tìm các vectơ hiệu: NC→−MC→;   AC→−BC→;  AB→−ME→.

    c) Chứng minh AM→+AN→=AB→+AD→. 

    Lời giải:

    M là trung điểm của BC nên BM = MC = 12BC.

    N là trung điểm của AD nên AN = ND = 12AD.

    Do ABCD là hình bình hành nên BC = AD.

    Do đó BM = MC = AN = ND.

    Do CE→=AN→ nên CE = AN.

    Do đó BM = MC = AN = ND = CE.

    Khi đó ta có AMCN, NCED là các hình bình hành.

    a) +) Tính NC→+MC→:

    Ta có MC→=CE→ nên NC→+MC→=NC→+CE→=NE→.

    +) Tính AM→+CD→:

    Ta có AM→=NC→ nên AM→+CD→=NC→+CD→=ND→.

    +) Tính AD→+NC→:

    Ta có NC→=AM→ nên AD→+NC→=AD→+AM→=AE→.

    b) +) Tính NC→−MC→:

    Ta có NC→−MC→=NM→.

    +) Tính AC→−BC→:

    Ta có AC→−BC→=AB→.

    +) Tính AB→−ME→:

    Ta có ME→=AD→ nên AB→−ME→=AB→−AD→=DB→.

    c) Ta có AM→+AN→=AC→ và AB→+AD→=AC→.

    Do đó AM→+AN→=AB→+AD→.

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải Toán 10 trang 102 Tập 1

    Giải Toán 10 trang 103 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 1: Số gần đúng và sai số

    Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

    Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

    Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

    Bài tập cuối chương 6

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 191 22/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: