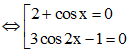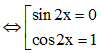Giải các phương trình sau: a) (2 + cos x)(3cos 2x – 1) = 0
Lời giải Bài 1.27 trang 24 SBT Toán 11 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.
Giải SBT Toán 11 Bài 4: Phương trình lượng giác cơ bản
Bài 1.27 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:
a) (2 + cos x)(3cos 2x – 1) = 0;
b) 2sin 2x – sin 4x = 0;
c) cos6 x – sin6 x = 0;
d) tan 2x cot x = 1.
Lời giải:
a) Ta có (2 + cos x)(3cos 2x – 1) = 0
+ Phương trình 2 + cos x = 0 vô nghiệm vì – 1 ≤ cos x ≤ 1.
+ Gọi α là góc thoả mãn cos α = . Ta có
3cos 2x – 1 = 0 ⇔ cos 2x = cos α ⇔ 2x = ± α + k2π (k ∈ ℤ) ⇔ x = + kπ (k ∈ ℤ).
Vậy nghiệm của phương trình đã cho là x = + kπ (k ∈ ℤ) với cos α = .
b) Ta có 2sin 2x – sin 4x = 0
⇔ 2sin 2x – 2sin 2x cos 2x = 0
⇔ 2sin 2x(1 – cos2x) = 0
Do sin2 2x + cos2 2x = 1 nên cos 2x = 1 kéo theo sin 2x = 0, do đó phương trình đã cho tương đương với
sin 2x = 0 ⇔ 2x = kπ (k ∈ ℤ) .
c) Ta có cos6 x – sin6 x = 0
⇔ cos6 x = sin6 x
⇔ (cos2 x)3 = (sin2 x)3
⇔ cos2 x = sin2 x
⇔ cos2 x – sin2 x = 0
⇔ cos 2x = 0
Từ đó ta được 2x = + kπ (k ∈ ℤ) hay .
d) Điều kiện sin x ≠ 0 và cos 2x ≠ 0.
Ta có tan 2x cot x = 1
⇔ tan 2x = tan x
⇔ 2x = x + kπ (k ∈ ℤ)
⇔ x = kπ (k ∈ ℤ).
Ta thấy x = kπ (k ∈ ℤ) không thoả mãn điều kiện sin x ≠ 0.
Vậy phương trình đã cho vô nghiệm.
Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:
Bài 1.25 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau: a) ;...
Bài 1.26 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau: a) sin(2x + 15°) + cos(2x – 15°) = 0;...
Bài 1.27 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau: a) (2 + cos x)(3cos 2x – 1) = 0;...
Bài 1.30 trang 25 SBT Toán 11 Tập 1: Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t...
Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức