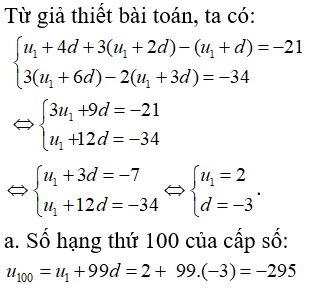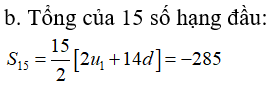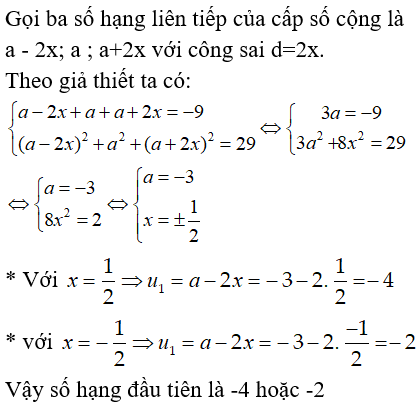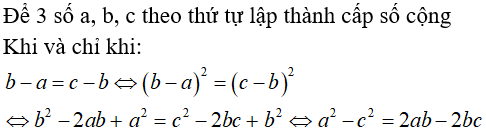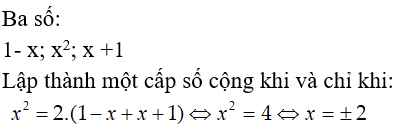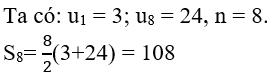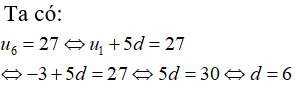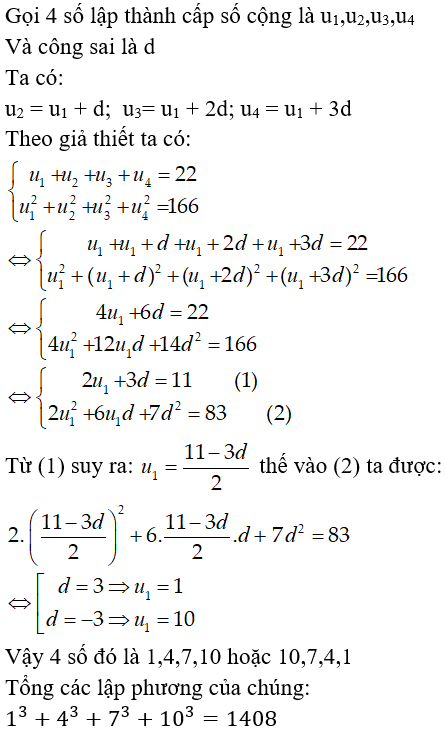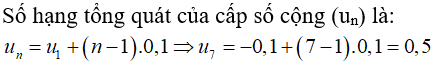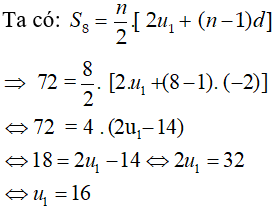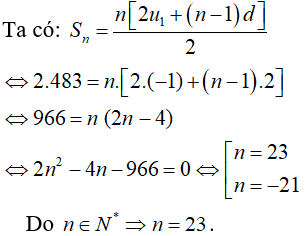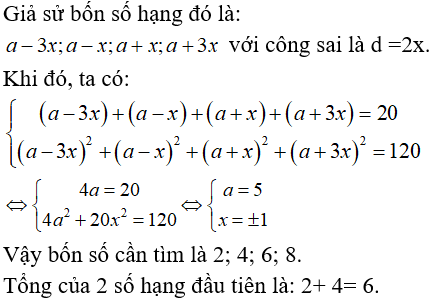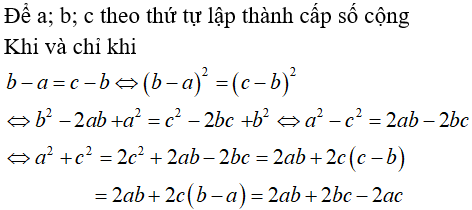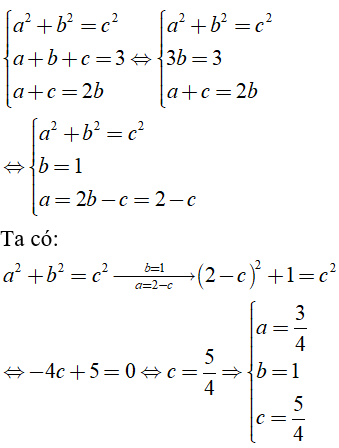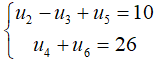Chuyên đề Dãy số (2022) - Toán 11

Chuyên đề Dãy số - Toán 11

A. Lý thuyết

I. Định nghĩa.

1. Định nghĩa dãy số.

Mỗi hàm số u xác định trên tập các số nguyên dương được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu:

$\begin{array}{l}u:{\mathbb{N}}^{*}\to ℝ\\ n\mapsto u\left(n\right)\end{array}$

Người ta thường viết dãy số dưới dạng khai triển: u₁, u₂, u₃,…,u_n,..,

Trong đó, u_n = u(n) hoặc viết tắt là (u_n), và gọi u₁ là số hạng đầu, u_n là số hạng thứ n và là số hạng tổng quát của dãy số.

- Ví dụ 1:

a) Dãy các số tự nhiên chẵn: 2; 4; 6; 8; …có số hạng đầu u₁ = 2, số hạng tổng quát là u_n = 2n.

b) Dãy các số tự nhiên chia hết cho 5 là 5; 10; 15; 20; … có số hạng đầu u₁ = 5, số hạng tổng quát là u_n = 5n.

2. Định nghĩa dãy số hữu hạn.

- Mỗi hàm số u xác định trên tập M = {1, 2, 3,.., m} với  được gọi là một dãy số hữu hạn.

- Dạng khai triển của nó là u₁, u₂, u₃,…, u_m, trong đó u₁ là số hạng đầu, u_m là số hạng cuối.

- Ví dụ 2.

a) 4, 7, 10, 13, 16, 19 là dãy số hữu hạn có u₁ = 4; u₆ = 19.

b) $1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6}$ là dãy số hữu hạn có u₁ = 4; u₆ = $\frac{1}{6}$.

II. Cách cho một dãy số.

1. Dãy số cho bằng công thức của số hạng tổng quát

- Ví dụ 3.

a) Cho dãy số (u_n) với u_n = n².   (1)

Từ công thức (1), ta có thể xác định được bất kì một số hạng nào của dãy số. Chẳng hạn, u₁₀ = 10² = 100.

Nếu viết dãy số này dưới dạng khai triển ta được:

1, 4, 9, 16, 25, 36,…, n²,….

b) Dãy số (u_n) với $u_n=\frac{{(-1)}^n}{n}$ có dạng khai triển là: $-1,\frac{1}{2},\frac{-1}{3},\frac{1}{4},\frac{-1}{5},$$\frac{1}{6},\mathrm{...},\frac{{(-1)}^n}{n},\mathrm{...}$

2. Dãy số cho bằng phương pháp mô tả

Ví dụ 4. Số là số thập phân vô hạn không tuần hoàn

Nếu lập dãy số (u_n) với u_n là giá trị gần đúng thiếu của số $\sqrt{2}$ với sai số tuyệt đối 10^-n thì:

u₁ = 1,4 ; u₂ = 1,41; u₃ = 1,414; u₄ = 1,4142,….

Đó là dãy số được cho bằng phương pháp mô tả, trong đó chỉ ra cách viết các số hạng liên tiếp của dãy.

3. Dãy số cho bằng phương pháp truy hồi

Cho một dãy số bằng phương pháp truy hồi, tức là:

a) Cho số hạng đầu (hay vài số hạng đầu).

b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.

- Ví dụ 5. Dãy số (u_n) được xác định như sau:

$\left\{\begin{array}{c}{u}_1=1;u_2=2\\ u_n=2u_{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}3u_{n-2}(n\ge 3)\end{array}\right.$

Dãy số như trên là dãy số cho bằng phương pháp truy hồi.

III. Biểu diễn hình học của dãy số.

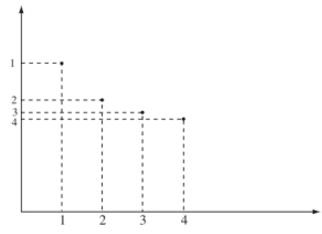
Vì dãy số là một hàm số trên nên ta có thể biểu diễn dãy số bằng đồ thị. Khi đó trong mặt phẳng tọa độ, dãy số được biểu diễn bằng các điểm có tọa độ (n ; u_n).

Ví dụ 6: Dãy số (u_n) với $u_n=\frac{n+1}{n}$ có biểu diễn hình học như sau:

IV. Dãy số tăng, dãy số giảm và dãy số bị chặn

1. Dãy số tăng, dãy số giảm.

- Định nghĩa 1:

Dãy số (u_n) được gọi là dãy số tăng nếu ta có u_{n +1} > u_n với mọi $n\in {\mathbb{N}}^{*}$.

Dãy số (u_n) được gọi là dãy số giảm nếu ta có u_{n +1} < u_n với mọi $n\in {\mathbb{N}}^{*}$.

- Ví dụ 7. Dãy số (u_n) với u_n = 2 – 2n là dãy số giảm.

Thật vậy, với mọi $n\in {\mathbb{N}}^{*}$ xét hiệu u_{n +1} – u_n. Ta có:

u_{n +1} – u_n = 2 – 2(n + 1) – (2 – 2n) = – 2  < 0

Do u_{n +1} – u_n < 0 nên u_{n +1} < u_n với mọi $n\in {\mathbb{N}}^{*}$

Vậy dãy số đã cho là dãy số giảm.

- Chú ý:

Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn dãy số (u_n) với u_n = (– 1)ⁿ tức là dãy: – 1, 1, – 1, 1, – 1, 1, – 1…không tăng cũng không giảm.

2. Dãy số bị chặn.

- Dãy số (u_n) được gọi là bị chặn trên nếu tồn tại một số M sao cho:

$u_n\le M,\forall n\in {\mathbb{N}}^{*}$

- Dãy số (u_n) được gọi là bị chặn dưới nếu tồn tại một số m sao cho:

$u_n\ge m,\forall n\in {\mathbb{N}}^{*}$

- Dãy số (u_n) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m; M sao cho:

$m\le u_n\le M,\forall n\in {\mathbb{N}}^{*}$

- Ví dụ 8. Dãy số (u_n) với $u_n=\frac{1}{n}$ bị chặn vì 0 < u_n ≤ 1.

B. Bài tập

I. Bài tập trắc nghiệm

Bài 1: Cho hai cấp số cộng (un): 4, 7, 10, 13, 16, ...và (vn):1, 6, 11, 16, 21, ...Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?

A.10

B. 20

C. 30

D. 40

Lời giải:

Ứng với 20 giá trị của t cho 20 giá trị của n và 20 giá trị của k.

Vậy có 20 số hạng chung của hai dãy

Chọn đáp án B

Bài 2: Cho cấp số cộng (un) thỏa mãn: .

a. Tính số hạng thứ 100 của cấp số ;

A. - 243

B. - 295

C. - 231

D. - 294

b. Tính tổng 15 số hạng đầu của cấp số ;

A. - 244

B. - 274

C. - 253

D. - 285

Lời giải:

Chọn đáp án B

Chọn đáp án D

Bài 3: Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên

A. -3 hoặc – 6

B. – 4 hoặc -2

C. -1 hoặc -5

D. -4 hoặc - 7

Lời giải:

Chọn đáp án B

Bài 4: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có góc nhỏ nhất bằng 25°. Tìm 2 góc còn lại?

A. 65° ; 90°.

B. 75° ; 80°.

C. 60° ; 95°.

D. 55°; 100°.

Lời giải:

Chọn đáp án C

Bài 5: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

A. a² + c² = 2ab + 2bc.

B. a² - c² = 2ab - 2bc.

C. a² + c² = 2ab - 2bc.

D. a² - c² = ab - bc.

Lời giải:

Chọn đáp án B

Bài 6: Tìm x để 3 số : 1 - x; x2 ; x + 1 theo thứ tự lập thành một cấp số cộng?

A. Không có giá trị nào của x.

B. x = ± 2 .

C. x = ± 1 .

D. x = 0

Lời giải:

Chọn đáp án B

Bài 7: Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng

a. un = 2n + 3

A. d = -2

B. d = 3

C. d = 5

D. d = 2

b. un = -3n + 1

A. d = -2

B. d = 3

C. d = -3

D. d = 1

c. un = n2 + 1

A. d = Ø

B. d = 3

C. d = -3

D. d = 1

d. un = 2/n

A. d = Ø

B. d = 1/2

C. d = -3

D. d = 1

Lời giải:

Bài 8: Cho cấp số cộng có 8 số hạng. Số hạng đầu bằng 3 số hạng cuối bằng 24. Tính tổng các số hạng này

A. 105

B. 27

C. 108

D. 111

Lời giải:

Chọn đáp án C

Bài 9: Cho một cấp số cộng có u1 = -3; u6 = 27. Tìm d ?

A. d = 5

B. d = 7

C. d = 6

D. d = 8

Lời giải:

Chọn đáp án C

Bài 10: Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :

A. 22

B. 166

C. 1752

D. 1408

Lời giải:

Chọn đáp án D

II. Bài tập tự luận có lời giải

Bài 1: Cho cấp số cộng (un) có: u1 = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:

Lời giải:

Bài 2: Cho cấp số cộng (un) thỏa: 

a. Xác định công thức tổng quát của cấp số

b. Tính S = u1 + u4 + u7 +...+ u2011.

Lời giải:

Bài 3: Cho dãy số (un) có d = –2; S8 = 72. Tính u1 ?

Lời giải:

Bài 4: Cho dãy số (un) có u1 = -1; d = 2; Sn = 483 Tính số các số hạng của cấp số cộng?

Lời giải:

Bài 5: Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tính tổng của hai số hạng đầu tiên?

Lời giải:

Bài 6: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

Lời giải:

Bài 7: Tìm x biết x² + 1, x - 2, 1 - 3x lập thành cấp số cộng ;

Lời giải:

Bài 8: Tìm m để phương trình x³ - 3x² - 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng.

Lời giải:

Bài 9: Phương trình x⁴ - 2(m + 1)x² + 2m + 1 = 0 (1) có bốn nghiệm phân biệt lập thành cấp số cộng.

Lời giải:

Bài 10: Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:

Lời giải:

Ba cạnh a, b, c ( a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa mãn yêu cầu thì:

III. Bài tập vận dụng

Bài 1: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế?

Bài 2 Cho các dãy số (u_n) sau :

Hỏi có bao nhiêu dãy số là cấp số cộng ?

Bài 3 Viết ba số xen giữa các số 2 và 22 để được cấp số cộng có 5 số hạng. Tính tổng của ba số viết xen giữa đó ?

Bài 4 Cho tứ giác ABCD biết 4 góc của tứ giác lập thành một cấp số cộng và góc A bằng 30°. Tìm công sai d ?

Bài 5 Cho cấp số cộng (u_n) thỏa mãn 

Bài 6 Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tính số hạng đầu và công sai của nó:

a) $u_n=5-2n$

b) $u_n=\frac{n}{2}-1$

c) $u_n=3^n$

d) $u_n=\frac{7-3n}{2}$

Bài 7 Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:

a) $\{\begin{array}{c}{u}_1-u_3+u_5=10\\ u_1+u_{6=17}\end{array}$,

b) $\{\begin{array}{c}{u}_7-u_3=8\\ u_2.u_7=75\end{array}$.

Bài 8 Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng $u_1,n,d,u_n,S_n$.

a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?

b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:

Bài 9 Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân $0,5m$. Cầu thang đi từ tầng một lên tầng $2$ gồm $21$ bậc, mỗi bậc cao $18cm$.

a) Hãy viết công thức để tìm độ cao của một bậc tuỳ ý so với mặt sân.

b) Tính độ cao của sàn tầng hai so với mặt sân.

Bài 10 Từ giờ đến giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?

Xem thêm các bài Chuyên đề Toán lớp 11 hay, chi tiết khác:

Chuyên đề Phương pháp quy nạp toán học

Chuyên đề Cấp số cộng

Chuyên đề Cấp số nhân

Chuyên đề Ôn tập chương 3

Chuyên đề Giới hạn của dãy số