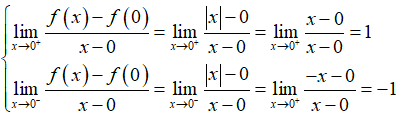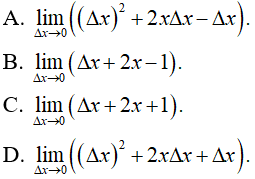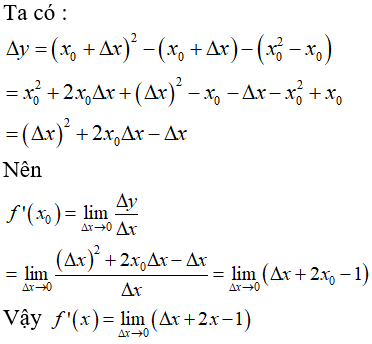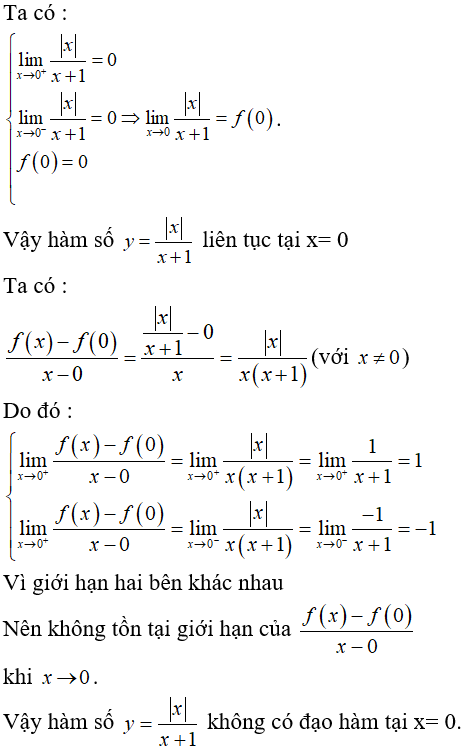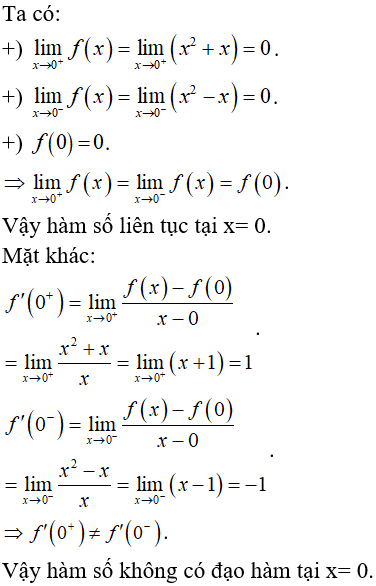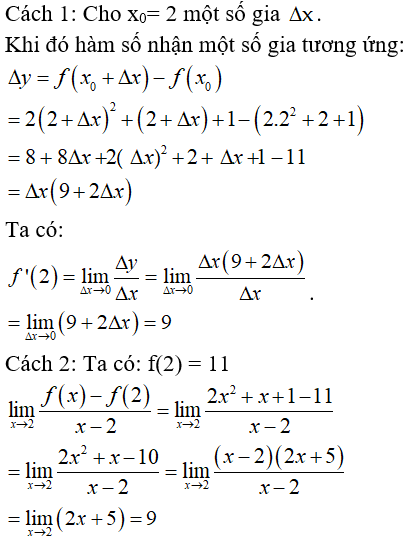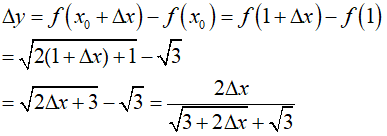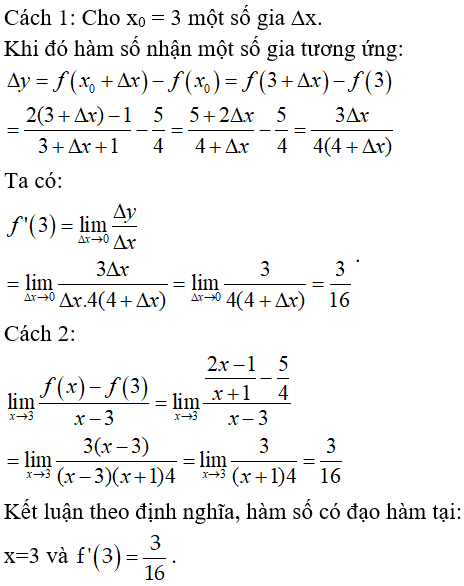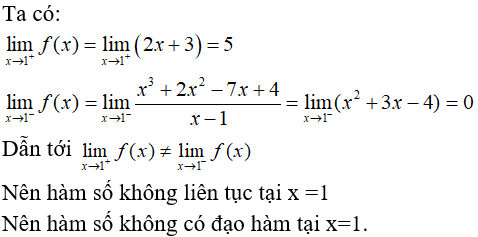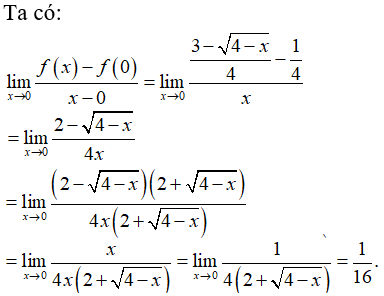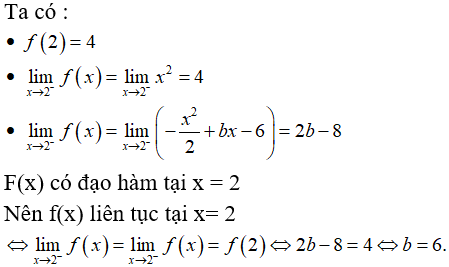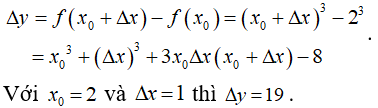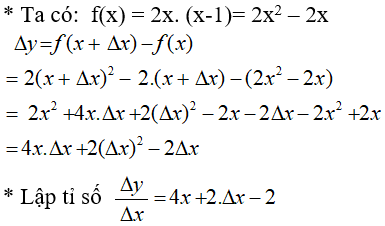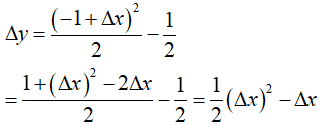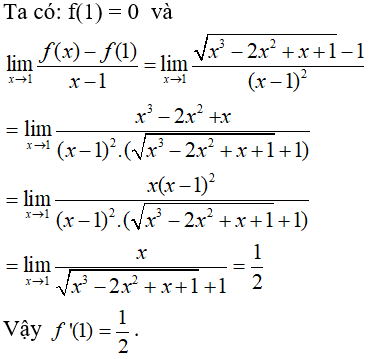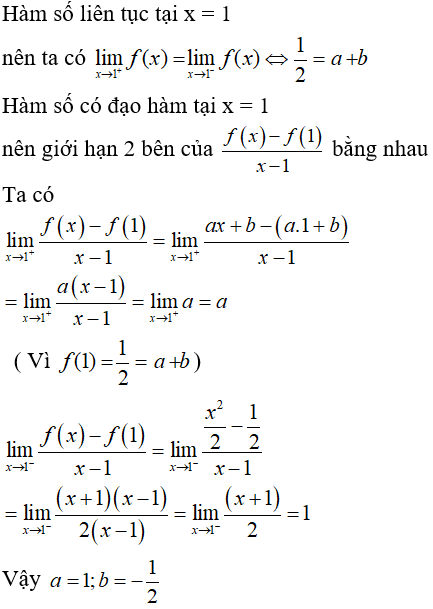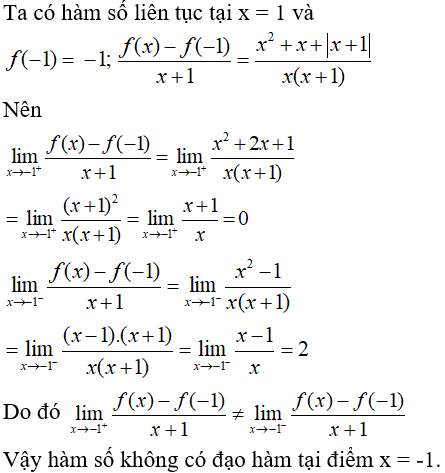Chuyên đề Định nghĩa và ý nghĩa của đạo hàm (2022) - Toán 11
Với Chuyên đề Định nghĩa và ý nghĩa của đạo hàm (2022) - Toán 11 mới nhất được biên soạn bám sát chương trình Toán 11 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Định nghĩa và ý nghĩa của đạo hàm - Toán 11
A. LÝ THUYẾT
I. Đạo hàm tại một điểm
1. Định nghĩa đạo hàm tại một điểm
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 thuộc (a; b). Nếu tồn tại giới hạn (hữu hạn): limx→x0f(x)−f(x0)x−x0 thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại điểm x0 và được kí hiệu là f'(x0). Vậy f'
* Chú ý:
Đại lượng ∆x = x- x0 được gọi là số gia của đối số tại x0.
Đại lượng ∆y= f(x) – f(x0)= f(x0 + ∆x) – f(x0) được gọi là số gia tương ứng của hàm số. Như vậy: .
2. Quy tắc tính đạo hàm bằng định nghĩa:
Để tính đạo hàm của hàm số y = f(x) tại điểm x0 bằng định nghĩa, ta có quy tắc sau đây:
+ Bước 1: Giả sử ∆x là số gia của đối số tại x0 tính:
∆y= f(x0 + ∆x) – f( x0) .
+ Bước 2: Lập tỉ số .
+ Bước 3: Tìm
Ví dụ 1. Cho hàm số , có là số gia của đối số tại x = 2. Khi đó bằng bao nhiêu.
Lời giải
Tập xác định của hàm số đã cho là: .
Giả sử ∆x là số gia của đối số tại x0 = 2. Ta có:
Khi đó:
Vậy f’(2) = 1.
3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số
Định lý 1. Nếu hàm số y= f( x) có đạo hàm tại x0 thì nó liên tục tại điểm đó.
Chú ý:
+ Nếu hàm số y= f(x) gián đoạn tại x0 thì hàm số không có đạo hàm tại điểm đó.
+ Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.
Ví dụ 2. Chẳng hạn hàm số liên tục tại x = 0 nhưng không có đạo hàm tại đó. Ta nhận xét rằng đồ thị của hàm số này là một đường liền, nhưng bị gãy tại điểm O(0;0) như hình vẽ sau:
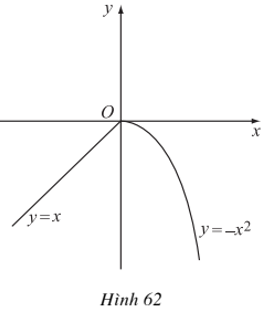
4. Ý nghĩa của đạo hàm
a) Ý nghĩa hình học của đạo hàm:
+) Định lí: Đạo hàm của hàm số y= f(x) tại điểm x = x0 là hệ số góc của tiếp tuyến M0T của đồ thị hàm số y= f( x) tại điểm M0(x0; f(x0)).
+) Định lí: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M0(x0; f(x0)) là:
y – y0= f’(x0) ( x- x0) trong đó y0= f(x0).
Ví dụ 3. Viết phương trình tiếp tuyến của đường cong y = x3 – 3x2 + 2 tại điểm có hoành độ x = 3.
Lời giải
Bằng định nghĩa ta tính được: y’(3) = 9.
Do đó hệ số góc của tiếp tuyến là 9.
Ta có: y(3) = 2.
Vậy phương trình tiếp tuyến của đường cong tại điểm có hoành độ x = 3 là:
y = 9(x – 3) + 2 = 9x – 27 + 2 = 9x – 25.
b) Ý nghĩa vật lý của đạo hàm:
+) Vận tốc tức thời:
Xét chuyển động thẳng xác định bởi phương trình: s= s(t); với s= s(t) là một hàm số có đạo hàm. Vận tốc tức thời tại thời điểm t0 là đạo hàm của hàm số s= s(t) tại t0: v(t0) = s’(t0).
+) Cường độ tức thời:
Nếu điện lượng Q truyền trong dây dẫn là một hàm số của thời gian: Q= Q(t) ( là hàm số có đạo hàm) thì cường độ tức thời của dòng điện tại thời điểm t0 là đạo hàm của hàm số Q= Q(t) tại t0: I(t0) = Q’(t0) .
Ví dụ 4. Một xe máy chuyển động theo phương trình : s(t)= t2 + 6t+ 10 trong đó t đơn vị là giây; s là quãng đường đi được đơn vị m. Tính vận tốc tức thời của xe tại thời điểm t= 3.
Lời giải
Phương trình vận tốc của xe là v( t)=s' ( t)=2t+6 ( m/s)
⇒ Vận tốc tức thời của xe tại thời điểm t= 3 là:
V(3)= 2.3+ 6 = 12 (m/s)
Chọn A.
II. Đạo hàm trên một khoảng
Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.
Khi đó ta gọi hàm số f’:
là đạo hàm của hàm số y = f(x) trên khoảng (a;b), kí hiệu là y’ hay f’(x).
Ví dụ 5. Hàm số y = x2 – 2x có đạo hàm y’ = 2x – 2 trên khoảng .
Hàm số có đạo hàm trên các khoảng và .
B. BÀI TẬP
I. Bài tập trắc nghiệm
Bài 1: Xét ba mệnh đề sau: (1) Nếu hàm số f(x) có đạo hàm tại điểm x = x0 thì f(x) liên tục tại điểm đó. (2) Nếu hàm số f(x) liên tục tại điểm x = x0 thì f(x) có đạo hàm tại điểm đó. (3) Nếu f(x) gián đoạn tại x = x0 thì chắc chắn f(x) không có đạo hàm tại điểm đó. Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Lời giải:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f(x) liên tục tại điểm x = x0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R.
Nhưng ta có
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.
Chọn đáp án A
Bài 2: Cho hàm số f(x) = x2 - x, đạo hàm của hàm số ứng với số gia của đối số x tại x0 là
Lời giải:
Chọn đáp án B
Bài 3: Xét hai câu sau: (1) Hàm số 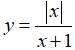
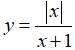
A. Chỉ có (2) đúng.
B. Chỉ có (1) đúng.
C. Cả hai đều đúng.
D. Cả hai đều sai.
Lời giải:
Chọn đáp án B
Bài 4: Cho hàm số f(x) = x2 + |x|. Xét hai câu sau: (1). Hàm số trên có đạo hàm tại x= 0 (2). Hàm số trên liên tục tại x= 0 Trong hai câu trên:
A. Chỉ (1) đúng.
B. Chỉ (2) đúng.
C. Cả hai đều đúng.
D. Cả hai đều sai.
Lời giải:
Chọn đáp án B
Bài 5: Tính đạo hàm của hàm số y = 2x2 + x + 1 tại điểm x = 2
A. 9
B. 4
C. 7
D. 6
Lời giải:
Kết luận theo định nghĩa, hàm số có đạo hàm tại x = 2 và f'(2) = 9.
Chọn đáp án A
Bài 6: Tính số gia của hàm số 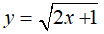
A.
B.
C.
D. Đáp án khác
Lời giải:
Cho x0 = 1 một số gia ∆x. Khi đó hàm số nhận một số gia tương ứng:
Chọn đáp án B
Bài 7: Tính đạo hàm của hàm số 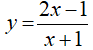
A. 1/6
B. 3/16
C. 2/9
D. 4/5
Lời giải:
Chọn đáp án B
Bài 8: Tính đạo hàm của hàm số 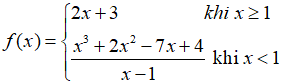
A. 0
B. 4
C. 5
D. Đáp án khác
Lời giải:
Chọn đáp án D
Bài 9: Cho hàm số 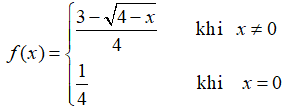
A. 1/4
B. 1/16
C. 1/32
D. Không tồn tại.
Lời giải:
Chọn đáp án B
Bài 10: Cho hàm số 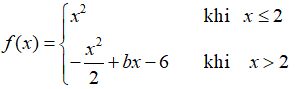
A. b = 3
B. b = -6
C. b = 1
D. b = 6
Lời giải:
Chọn đáp án D
II. Bài tập tự luận có giải
Bài 1: Cho hàm số y = f(x) có đạo hàm tại x0 là f'(x0) . Khẳng định nào sau đây sai?
Lời giải:
Bài 2: Số gia của hàm số f(x) = x3 ứng với x0 = 2 và Δx = 1 bằng bao nhiêu?
Lời giải:
Gọi ∆x là số gia của đối số và ∆y là số gia tương ứng của hàm số.
Ta có :
Bài 3: Tỉ số 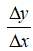
Lời giải:
Bài 4: Số gia của hàm số f(x) = x2/2 ứng với số gia Δx của đối số x tại x0 = -1 là
Lời giải:
Với số gia ∆x của đối số x tại x0 = -1 ,ta có:
Bài 5: Tính đạo hàm của hàm số 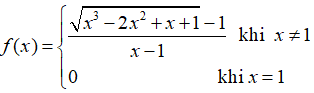
Lời giải:
Bài 6: Cho hàm số 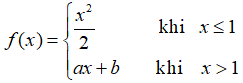
Lời giải:
Bài 7: Tính đạo hàm của hàm số 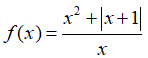
Lời giải:
Nhận xét: Hàm số y = f(x) có đạo hàm tại x = x0 thì phải liên tục tại điểm đó.
Bài 8: Tìm số gia của hàm số f(x) = x3, biết rằng:
Lời giải:
Số gia của hàm số được tính theo công thức:
Δy = f(x) – f(x0) = f(x0 + Δx) – f(x0)
a. Δy = f(1 + 1) – f(1) = f(2) – f(1) = 23 – 13 = 7
b. Δy = f(1 – 0,1) – f(1) = f(0,9) – f(1) = (0,9)3 – 13 = -0,271.
Bài 9

Lời giải:

Bài 10 Tính ( bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra:
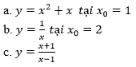
Lời giải:
y = x2 + x tại x0 = 1
*Giả sử Δx là số gia của đối số tại x0 = 1. Ta có:
∆Δy = f(x0+Δx)-f(x0) = f(1-Δx) = f(1)
= (1+Δx)2 +(1+Δx)-(12 +1)
= Δx(3+Δx)
* Δx/Δy = 3+x
* limΔx/Δy = lim(3-Δx) = 3(vớiΔx →0)
III. Bài tập vận dụng
Bài 1 Chứng minh rằng hàm số:
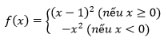
Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.
Bài 2 Viết phương trình tiếp tuyến đường cong y = x3
a. Tại điểm (-1; -1);
b. Tại điểm có hoành độ bằng 2;
c. Biết hệ số góc của tiếp tuyến bằng 3.
Bài 3 Viết phương trình tiếp tuyến của hypebol y = 1/x

Bài 4 Một vật rơi tự do theo phương trình s=1/2 gt2, trong đó g≈9,8m/s2 là gia tốc trọng trường.
a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến t+Δt, trong các trường hợp Δt = 0,1s; Δt = 0,05s; Δt = 0,001s.
b. Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.
Bài 5 Tìm số gia của hàm số , biết rằng :
a)
b)
Bài 6 Tính và của các hàm số sau theo và :
| a) ; | b) ; |
| c) ; | d) |
Bài 7 Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau tại các điểm đã chỉ ra:
a) tại ;
b) tại ;
c) tại .
Bài 8 Chứng minh rằng hàm số
không có đạo hàm tại điểm nhưng có đạo hàm tại điểm .
Bài 9 Viết phương trình tiếp tuyến của đường cong :
a) Tại điểm có tọa độ ;
b) Tại điểm có hoành độ bằng ;
c) Biết hệ số góc của tiếp tuyến bằng
Bài 10 Viết phương trình tiếp tuyến của đường hypebol :
a) Tại điểm
b) Tại điểm có hoành độ bằng ;
c) Biết rằng hệ số góc của tiếp tuyến bằng -.
Xem thêm các bài Chuyên đề Toán lớp 11 hay, chi tiết khác:
Chuyên đề Quy tắc tính đạo hàm
Xem thêm các chương trình khác:
- Giải sgk Hóa học 11 | Giải bài tập Hóa học 11 Học kì 1, Học kì 2 (Sách mới)
- Lý thuyết Hóa học 11(sách mới) | Kiến thức trọng tâm Hóa 11
- Giải sbt Hóa học 11 (sách mới) | Sách bài tập Hóa học 11
- Các dạng bài tập Hóa học lớp 11
- Giáo án Hóa học lớp 11 mới nhất
- Tóm tắt tác phẩm Ngữ văn 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 11 (hay nhất) | Để học tốt Ngữ Văn 11 (sách mới)
- Soạn văn 11 (ngắn nhất) | Để học tốt Ngữ văn 11 (sách mới)
- Tác giả tác phẩm Ngữ văn 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Văn mẫu 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 11 (thí điểm)
- Giải sgk Tiếng Anh 11 | Giải bài tập Tiếng anh 11 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 11 (sách mới) | Sách bài tập Tiếng Anh 11
- Giải sbt Tiếng Anh 11 (thí điểm)
- Giải sgk Lịch sử 11 | Giải bài tập Lịch sử 11 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch Sử 11(sách mới) | Kiến thức trọng tâm Lịch Sử 11
- Giải Tập bản đồ Lịch sử 11
- Giải sgk Vật Lí 11 | Giải bài tập Vật lí 11 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Vật Lí 11 (sách mới) | Sách bài tập Vật Lí 11
- Lý thuyết Vật Lí 11 (sách mới) | Kiến thức trọng tâm Vật Lí 11
- Các dạng bài tập Vật Lí lớp 11
- Giáo án Vật lí lớp 11 mới nhất
- Giải sgk Sinh học 11 | Giải bài tập Sinh học 11 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Sinh học 11 (sách mới) | Kiến thức trọng tâm Sinh 11
- Giải sgk Giáo dục công dân 11
- Lý thuyết Giáo dục công dân 11
- Lý thuyết Địa Lí 11 (sách mới) | Kiến thức trọng tâm Địa lí 11
- Giải Tập bản đồ Địa Lí 11
- Giải sgk Giáo dục quốc phòng - an ninh 11