Nội dung bài viết

    Xem thêm

    Chuyên đề Vectơ trong không gian. Quan hệ vuông góc trong không gian mới nhất - Toán 11

     Với Chuyên đề Toán 11 Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian mới nhất được biên soạn bám sát chương trình Toán lớp 11 giúp bạn học tốt môn Toán hơn.

    1 633 27/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Chuyên đề Toán 11 Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian

    Chuyên đề Vectơ trong không gian

    Xem chi tiết 

    Chuyên đề Hai đường thẳng vuông góc

    Xem chi tiết 

    Chuyên đề Đường thẳng vuông góc với mặt phẳng

    Xem chi tiết 

    Chuyên đề Hai mặt phẳng vuông góc

    Xem chi tiết 

    Chuyên đề Khoảng cách

    Xem chi tiết 

    Chuyên đề Ôn tập chương 3

    Xem chi tiết 

    Xem thêm các bài Giáo án Toán lớp 4 hay, chi tiết khác:

    Chương 3: Dãy số - Cấp số cộng và cấp số nhân

    Chương 4: Giới hạn

    Chương 5: Đạo hàm

    Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

    Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

    --------------------------------------------------------

    Chuyên đề Vectơ trong không gian - Toán 11

    A. Lý thuyết.

    I. Định nghĩa và các phép toán về vecto trong không gian.

    Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B ta có một vecto, được kí hiệu là →AB.

    1. Định nghĩa.

    - Vecto trong không gian là một đoạn thẳng có hướng. Kí hiệu →AB chỉ vecto có điểm đầu là A, điểm cuối là B. Vecto còn được kí hiệu là →a;  →b;  →x;  →y....

    - Các khái niệm liên quan đến vecto như giá của vecto, độ dài của vecto, sự cùng phương, cùng hướng của vecto, vecto – không, sự bằng nhau của hai vecto … được định nghĩa tương tự như trong mặt phẳng.

    2. Phép cộng và phép trừ vecto trong không gian

    - Phép cộng và phép trừ của hai vecto trong không gian được định nghĩa tương tự như phép cộng và phép trừ hai vecto trong mặt phẳng.

    - Phép cộng vecto trong không gian cũng có các tính chất như phép cộng vecto trong mặt phẳng. Khi thực hiện phép cộng vecto trong không gian ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vecto trong hình học phẳng.

    Ví dụ 1. Cho tứ diện ABCD. Chứng minh →DA +​  →BC =  →BA  +​  →DC

    Lời giải:

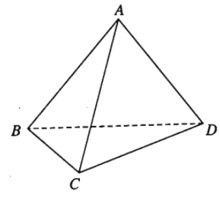
    Lý thuyết Vectơ trong không gian chi tiết – Toán lớp 11 (ảnh 1)

    Áp dụng quy tắc ba điểm ta có: →DA  = →DC + →CA

    Ta có: 

    →DA +​  →BC = →DC + →CA   +​  →BC=  →DC +​  (→BC +​  →CA)=  →DC  +​  →BA

    ( điều phải chứng minh).

    II. Điều kiện đồng phẳng của ba vecto.

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 633 27/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: