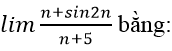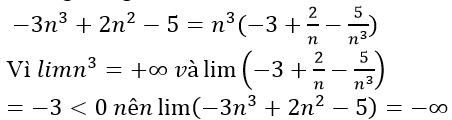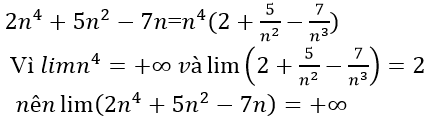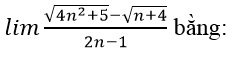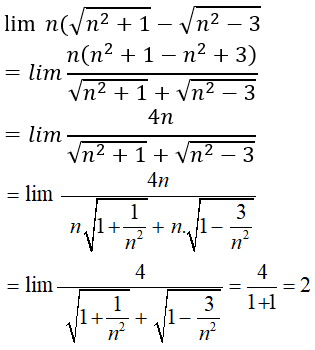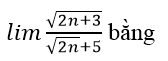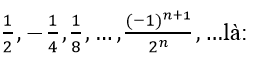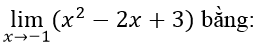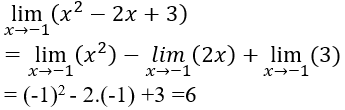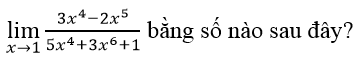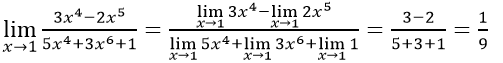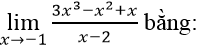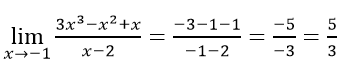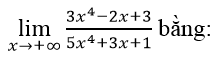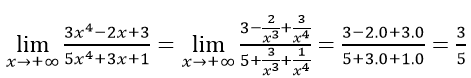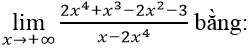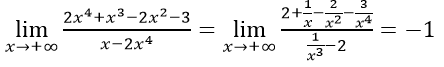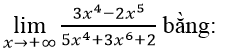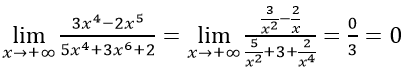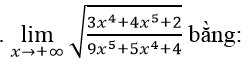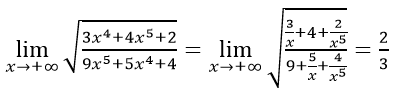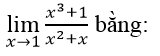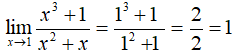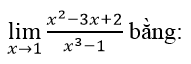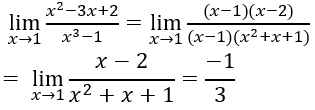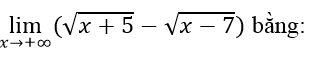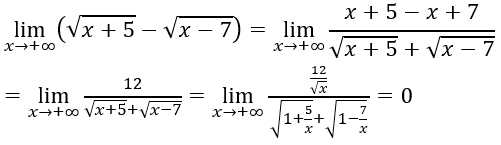Chuyên đề Ôn tập chương 4 (2022) - Toán 11

Chuyên đề Ôn tập chương 4 - Toán 11

A. LÝ THUYẾT

1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

+) Ta nói dãy số (u_n) có giới hạn là 0 khi n dần tới dương vô cực, nếu |u_n| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.

Kí hiệu: $\underset{\mathrm{n}\to +\infty }{\lim }{\mathrm{u}}_{\mathrm{n}}=0$ hay u_n → 0 khi n → +∞.

+) Ta nói dãy số (v_n) có giới hạn là a (hay v_n dần tới a) khi n → +∞ nếu $\underset{\mathrm{n}\to +\infty }{\lim }\left({\mathrm{v}}_{\mathrm{n}}-\mathrm{a}\right)=0$

Kí hiệu: $\underset{\mathrm{n}\to +\infty }{\lim }{\mathrm{v}}_{\mathrm{n}}=\mathrm{a}$ hay v_n → a khi n → +∞.

Một vài giới hạn đặc biệt

a) $\underset{\mathrm{n}\to +\infty }{\lim }\frac{1}{\mathrm{n}}=0,\underset{\mathrm{n}\to +\infty }{\lim }\frac{1}{{\mathrm{n}}^{\mathrm{k}}}=0$ với k nguyên dương;

b) $\underset{\mathrm{n}\to +\infty }{\lim }{\mathrm{q}}^{\mathrm{n}}$ nếu |q| < 1;

c) Nếu u_n = c (c là hằng số) thì $\underset{\mathrm{n}\to +\infty }{\lim }{\mathrm{u}}_{\mathrm{n}}=\underset{\mathrm{n}\to +\infty }{\lim }\mathrm{c}=\mathrm{c}$.

Chú ý: Từ nay về sau thay cho $\underset{\mathrm{n}\to +\infty }{\lim }{\mathrm{u}}_{\mathrm{n}}=\mathrm{a}$ ta viết tắt là lim u_n = a.

II. ĐỊNH LÝ VỀ GIỚI HẠN HỮU HẠN

+) Định lí 1

a) Nếu lim u_n = a và lim v_n = b thì

lim (u_n + v_n) = a + b

lim (u_n – v_n) = a – b

lim (u_n.v_n) = a.b

$\lim \frac{{\mathrm{u}}_{\mathrm{n}}}{{\mathrm{v}}_{\mathrm{n}}}=\frac{\mathrm{a}}{\mathrm{b}}$ (nếu $\mathrm{b}\ne 0$)

Nếu ${\mathrm{u}}_{\mathrm{n}}\ge 0$ với mọi n và limu_n­ = a thì:

$\lim \sqrt{{\mathrm{u}}_{\mathrm{n}}}=\sqrt{\mathrm{a}}$ và $\mathrm{a}\ge 0.$

III. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN

Cấp số nhân vô hạn (u_n) có công bội q, với |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn:

$\mathrm{S}={\mathrm{u}}_1+{\mathrm{u}}_2+{\mathrm{u}}_3+...+{\mathrm{u}}_{\mathrm{n}}+...$

$=\frac{{\mathrm{u}}_1}{1-\mathrm{q}}\left(\left|\mathrm{q}\right|<1\right)$

IV. GIỚI HẠN VÔ CỰC

1. Định nghĩa

- Ta nói dãy số (u_n) có giới hạn là +∞ khi n → +∞, nếu u_n có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Kí hiệu: lim u_n = +∞ hay u_n → +∞ khi n → +∞.

- Dãy số (u_n) có giới hạn là –∞ khi n → +∞, nếu lim (–u_n) = +∞.

Kí hiệu: lim u_n = –∞ hay u_n → –∞ khi n → +∞.

Nhận xét: u_n = +∞ ⇔ lim(–u_n) = –∞

2. Một vài giới hạn đặc biệt

Ta thừa nhận các kết quả sau

a) lim n^k = +∞ với k nguyên dương;

b) lim qⁿ = +∞ nếu q > 1.

3. Định lí 2

a) Nếu lim u_n = a và lim v_n = ±∞ thì $\lim \frac{{\mathrm{u}}_{\mathrm{n}}}{{\mathrm{v}}_{\mathrm{n}}}=0$

b) Nếu lim u_n = a > 0, lim v_n = 0 và v_n > 0, ∀ n > 0 thì $\lim \frac{{\mathrm{u}}_{\mathrm{n}}}{{\mathrm{v}}_{\mathrm{n}}}=+\infty$

c) Nếu lim u_n = +∞ và lim v_n = a > 0 thì ${\mathrm{limu}}_{\mathrm{n}}.{\mathrm{v}}_{\mathrm{n}}=+\infty$.

V. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM

1. Định nghĩa

Cho khoảng K chứa điểm x₀ và hàm số y = f(x) xác định trên K hoặc trên K \ {x₀}.

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n K \{x₀} và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to \infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$ hay f(x) → L khi x → x₀.

Nhận xét: $\underset{\mathrm{x}\to \infty }{\lim }\mathrm{x}={\mathrm{x}}_0,\underset{\mathrm{x}\to \infty }{\lim }\mathrm{c}=\mathrm{c}$ với c là hằng số

2. Định lí về giới hạn hữu hạn

Định lí 1

a) Giả sử $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$ và $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{g}\left(\mathrm{x}\right)=\mathrm{M}$. Khi đó:

$$\begin{gathered} \underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\left[\mathrm{f}\left(\mathrm{x}\right)+\mathrm{g}\left(\mathrm{x}\right)\right]=\mathrm{L}+\mathrm{M}; \\ \underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\left[\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right]=\mathrm{L}-\mathrm{M}; \\ \underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right).\mathrm{g}\left(\mathrm{x}\right)=\mathrm{L}.\mathrm{M}; \\ \underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}=\frac{\mathrm{L}}{\mathrm{M}}\left(\mathrm{M}\ne 0\right); \end{gathered}$$

b) Nếu $\mathrm{f}\left(\mathrm{x}\right)\ge 0$ và $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$ thì $\mathrm{L}\ge 0$ và $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\sqrt{\mathrm{f}\left(\mathrm{x}\right)}=\sqrt{\mathrm{L}}.$

(Dấu của f(x) được xét trên khoảng đang tìm giới hạn với $\mathrm{x}\ne {\mathrm{x}}_0$).

3. Giới hạn một bên

Định nghĩa 2

- Cho hàm số y = f(x) xác định trên (x₀; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to {\mathrm{x}}_0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$.

- Cho hàm số y = f(x) xác định trên (a; x₀).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, a < x_n < x₀ và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to {\mathrm{x}}_0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$.

Định lí 2

$\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}\iff \underset{\mathrm{x}\to {\mathrm{x}}_0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to {\mathrm{x}}_0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$

VI. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC

Định nghĩa 3

a) Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to +\infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$

b) Cho hàm số y = f(x) xác định trên (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (x_n) bất kì, x_n < a và x_n → –∞, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to -\infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$

Chú ý:

a) Với c, k là hằng số và k nguyên dương, ta luôn có:

$\underset{\mathrm{x}\to +\infty }{\lim }\mathrm{c}=\mathrm{c};\underset{\mathrm{x}\to -\infty }{\lim }\mathrm{c}=\mathrm{c};$$\underset{\mathrm{x}\to +\infty }{\lim }\frac{\mathrm{c}}{{\mathrm{x}}^{\mathrm{k}}}=0;\underset{\mathrm{x}\to -\infty }{\lim }\frac{\mathrm{c}}{{\mathrm{x}}^{\mathrm{k}}}=0.$

b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x₀ vẫn còn đúng khi x_n → +∞ hoặc x → –∞

VII. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ

1. Giới hạn vô cực

Định nghĩa 4

Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → –∞

Kí hiệu: $\underset{\mathrm{x}\to \infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=-\infty$

Nhận xét:

 $$\begin{gathered} \underset{\mathrm{x}\to +\infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=+\infty \\ \iff \underset{\mathrm{x}\to +\infty }{\lim }\left(-\mathrm{f}\left(\mathrm{x}\right)\right)=-\infty \end{gathered}$$

2. Một vài giới hạn đặc biệt

a) $\underset{\mathrm{x}\to +\infty }{\lim }{\mathrm{x}}^{\mathrm{k}}=+\infty$ với k nguyên dương.

b) Nếu k chẵn thì $\underset{\mathrm{x}\to -\infty }{\lim }{\mathrm{x}}^{\mathrm{k}}=+\infty$;

Nếu k lẻ thì $\underset{\mathrm{x}\to -\infty }{\lim }{\mathrm{x}}^{\mathrm{k}}=-\infty$.

3. Một vài quy tắc về giới hạn vô cực

a) Quy tắc tìm giới hạn của tích f(x).g(x)

b) Quy tắc tìm giới hạn của thương $\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}$

(Dấu của g(x) xét trên một khoảng K nào đó đang tính giới hạn, với $\mathrm{x}\ne {\mathrm{x}}_0$)

Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp:

$\mathrm{x}\to {\mathrm{x}}_0^{+},\mathrm{x}\to {\mathrm{x}}_0^{-};\mathrm{x}\to +\infty ;\mathrm{x}\to -\infty .$

B. Bài tập

I. Bài tập trắc nghiệm

Bài 1:

A. $\frac{2}{5}$   

B. $\frac{1}{5}$    

C. 0    

D. 1

Lời giải:

Chia cả tử thức mẫu thức cho n , ta có:

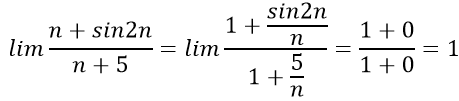
Chọn đáp án D

Bài 2: lim⁡(-3n³+2n²-5) bằng:

A. -3    

B. 0    

C. -∞    

D. +∞

Lời giải:

Ta có:

Chọn đáp án C

Bài 3: Lim(2n⁴+5n²-7n) bằng

A. -∞    

B. 0    

C. 2    

D. +∞

Lời giải:

Ta có:

Chọn đáp án D

Bài 4: Dãy số nào sau đây có giưới hạn là +∞?

A. un = 9n²-2n⁵    

B. un = n⁴-4n⁵

C. un = 4n²-3n    

D. un = n³-5n⁴

Lời giải:

Chỉ có dãy un = 4n²-3n có giới hạn là +∞, các dãy còn lại đều có giới hạn là -∞. Đáp án C

Thật vậy, ta có:

Chọn đáp án C

Bài 5: Nếu limun = L,un+9>0 ∀n thì lim√(un+9) bằng số nào sau đây?

A. L+9    

B. L+3    

C. √(L+9)    

D. √L+3

Lời giải:

Vì limun = L nên lim⁡(un + 9) = L + 9 do đó lim√(un + 9)=√(L + 9)

Chọn đáp án C

Bài 6:

A. 0    

B. 1    

C. 2    

D. +∞

Lời giải:

- Cách 1: Chia tử thức và mẫu thức cho n:

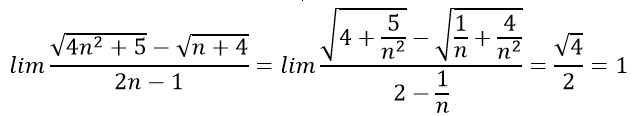
Đáp án là B

- Cách 2: Thực chất có thể coi bậc cao nhất của tử thức và mẫu thức là 1, do đó chỉ cần để ý hệ số bậc 1 của tử thức là √4, của mẫu thức là 2, từ đó tính được kết quả bằng 1.

Chọn đáp án B

Bài 7: lim⁡n(√(n²+1)-√(n²-3)) bằng:

A. +∞    

B. 4    

C. 2    

D. -1

Lời giải:

Chọn đáp án C

Bài 8:

A. $\frac{5}{7}$     

B. $\frac{5}{2}$  

C. 1      

D.+∞

Lời giải:

Chia cả tử và mẫu của phân thức cho √n, ta được:

Chọn đáp án C

Bài 9: Tổng của cấp số nhân vô hạn :

A. 1      

B. $\frac{1}{3}$      

C. $-\frac{1}{3}$      

D. $\frac{-2}{3}$

Lời giải:

Chọn đáp án B

Bài 10: Cho số thập phân vô hạn tuần hoàn a = 2,151515... (chu kỳ 15), a được biểu diễn dưới dạng phân số tối giản, trong đó m, n là các số nguyên dương. Tìm tổng m + n.

A. 104

B. 312

C. 38

D . 114

Lời giải:

Chọn đáp án A

II. Bài tập tự luận có lời giải

Bài 1:

Lời giải:

Bài 2:

Lời giải:

Bài 3:

Lời giải:

Bài 4:

Lời giải:

Chia cả tử và mẫu của phân thức cho x4 ta có

Bài 5:

Lời giải:

Bài 6:

Lời giải:

Bài 7:

Lời giải:

Bài 8:

Lời giải:

Bài 9:

Lời giải:

Bài 10:

Lời giải:

III. Bài tập vận dụng

Bài 1 Chứng minh rằng phương trình:

a. 2x³ – 6x + 1 = 0 có ít nhất hai nghiệm.

b. cos x = x có nghiệm

Bài 2 Cho hàm số $f(x)=\{\begin{array}{cc}3x+2;& x<-1\\ x^2-1& x\ge -1\end{array}$

a) Vẽ đồ thị của hàm số $y=f(x)$. Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.

b) Khẳng định nhận xét trên bằng một chứng minh.

Bài 3 a. Xét tính liên tục của hàm số $y=g(x)$ tại $x_0=2$, biết 

$g(x)=\{\begin{array}{cc}\frac{x^3-8}{x-2};& x\ne 2\\ 5;& x=2\end{array}$.

b. Trong biểu thức xác định $g(x)$ ở trên, cần thay số $5$ bởi số nào để hàm số liên tục tại $x_0=2$.

Bài 4 Cho hàm số $f(x)=\frac{x+1}{x^2+x-6}$ và $g(x)=tanx+sinx$.

Bài 5 Ý kiến sau đúng hay sai ?

"Nếu hàm số $y=f(x)$ liên tục tại điểm $x_0$ còn hàm số $y=g(x)$ không liên tục tại $x_0$ thì 
$y=f(x)+g(x)$ là một hàm số không liên tục tại $x_0$" 

Bài 6 Chứng minh rằng phương trình:

a) $2x^3-6x+1=0$ có ít nhất hai nghiệm;

b) $cosx=x$ có nghiệm.

Bài 7 Cho hàm số 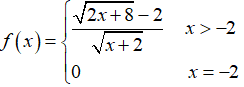. Tìm khẳng định đúng trong các khẳng định sau:

Bài 8 Cho hàm số 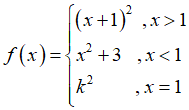. Tìm k để f(x) gián đoạn tại x= 1

Bài 9 Cho hàm số 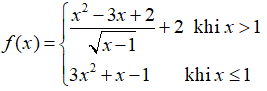. Khẳng định nào sau đây đúng nhất

Bài 10 Chọn giá trị f(0) để các hàm số 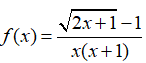 liên tục tại điểm x= 0.

Xem thêm các bài Chuyên đề Toán lớp 11 hay, chi tiết khác:

Chuyên đề Giới hạn của dãy số

Chuyên đề Giới hạn của hàm số

Chuyên đề Hàm số liên tục

Chuyên đề Định nghĩa và ý nghĩa của đạo hàm

Chuyên đề Quy tắc tính đạo hàm