Nội dung bài viết

    Xem thêm

    Chứng minh rằng các trung điểm của bốn cạnh của một hình

    Với giải bài 75 trang 106 sgk Toán lớp 8 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

    1 530 30/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Bài 11: Hình thoi

    Video Giải Bài 75 trang 106 Toán 8 Tập 1

    Bài 75 trang 106 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.

    *Lời giải

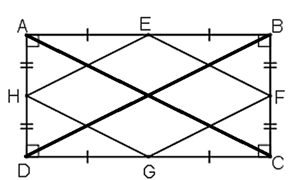
    Tài liệu VietJack

    +) Xét tam giác ABD có:

    E là trung điểm của AB

    H là trung điểm của AD

    ⇒ EH là đường trung bình của tam giác ADB

    ⇒EH=BD2(1)

    +) Xét tam giác ABC có:

    E là trung điểm của AB

    F là trung điểm của BC

    ⇒ EF là đường trung bình của tam giác ABC

    ⇒EF=AC2(2)

    +) Xét tam giác BCD có:

    F là trung điểm của BC

    G là trung điểm của DC

    ⇒ FG là đường trung bình của tam giác BCD

    ⇒FG=BD2(3)

    +) Xét tam giác CDA có:

    H là trung điểm của AD

    G là trung điểm của DC

    ⇒ HG là đường trung bình của tam giác CDA

    ⇒HG=AC2(4)

    Ta lại có ABCD là hình chữ nhật nên AC = BD (5)

    Từ (1), (2), (3), (4) và (5) suy ra EF = FG = GH= HE

    ⇒Tứ giác EFGH là hình thoi.

    *Phương pháp giải

    - Nhận thấy rất nhiều trung điểm: ta sẽ dùng tính chất đường trùng bình ở đây để suy ra các cặp cạnh bằng nhau

    - Vận dụng khái niệm và dấu hiện nhận biết hình thoi: ví dụ: Hình thoi là hình có các cạnh bằng nhau.

    *Lý thuyết cần nắm và dạng bài toán về hình chữ nhật, hình thoi:

    a) Hình thoi là tứ giác có bốn cạnh bằng nhau.

    Hình thoi là gì ? Định nghĩa, Tính chất về Hình thoi chi tiết

    Tính chất

    - Các cạnh đối song song

    - Các góc đối bằng nhau

    - Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường

    - Hai đường chéo là các đường phân giác của các góc ở đỉnh.

    Dấu hiệu nhận biết hình thoi

    - Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

    - Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

    - Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

    Các dạng bài tập và phương pháp giải

    Dạng 1. Chứng minh tứ giác là hình thoi

    Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình thoi

    Dạng 2. Vận dụng tính chất của hình thoi để chứng minh các tính chất hình học

    Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình thoi

    Dạng 3. Tìm điều kiện để tứ giác là hình thoi

    Phương pháp giải: Vận dụng định nghĩa, các tính chất và dấu hiệu nhận biết của hình thoi

    b) Hình chữ nhật là tứ giác có bốn góc vuông.

    Lý thuyết Hình chữ nhật – Toán lớp 8 Kết nối tri thức (ảnh 1)

    Chú ý: Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông và tứ giác đó là hình chữ nhật.

    Tính chất

    Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

    Nhận xét: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

    Dấu hiệu nhận biết

    - Hình bình hành có một góc vuông là hình chữ nhật

    - Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật

    Áp dụng vào tam giác vuông:

    a) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

    b) Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.

    Các dạng toán và ví dụ minh họa

    Dạng 1: Chứng minh tứ giác là hình chữ nhật

    Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình chữ nhật.

    a) Tứ giác có ba góc vuông là hình chữ nhật.

    b) Hình thang cân có một góc vuông là hình chữ nhật.

    c) Hình bình hành có một góc vuông là hình chữ nhật.

    d) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

    Xem thêm các bài viết liên quan hay, chi tiết:

    Lý thuyết Hình thoi – Toán lớp 8 Cánh diều

    Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

    Câu hỏi 1 trang 104 Toán 8 Tập 1: Chứng minh rằng tứ giác ABCD trên Hình 100...

    Câu hỏi 2 trang 104 Toán 8 Tập 1: Cho hình thoi ABCD, hai đường chéo cắt nhau tại O...

    Câu hỏi 3 trang 105 Toán 8 Tập 1: Hãy chứng minh dấu hiệu nhận biết 3...

    Bài 73 trang 105 Toán 8 Tập 1: Tìm các hình thoi trên hình 102...

    Bài 74 trang 106 Toán 8 Tập 1: Hai đường chéo của một hình thoi bằng 8cm và 10cm...

    Bài 76 trang 106 Toán Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi...

    Bài 77 trang 106 Toán 8 Tập 1: Chứng minh rằng: a) Giao điểm hai đường chéo...

    Bài 78 trang 106 Toán Tập 1: Đố. Hình 103 biểu diễn một phần của cửa xếp...

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 530 30/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: