Nội dung bài viết

    Xem thêm

    Bài 6 trang 118 Toán 7 Tập 2 | Cánh diều Giải Toán lớp 7

    Lời giải Bài 6 trang 118 Toán 7 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 499 01/03/2023
    Trang trước
    Trang sau  

    Giải Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác

    Bài 6 trang 118 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:

    a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;

    b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

    Lời giải:

    a)

    GT

    ∆ABC đều,

    G là trọng tâm,

    H là trực tâm,

    I là giao điểm của ba đường phân giác,

    O là giao điểm của ba đường trung trực.

    KL

    Bốn điểm G, H, I, O trùng nhau.

    Chứng minh (Hình vẽ dưới đây):

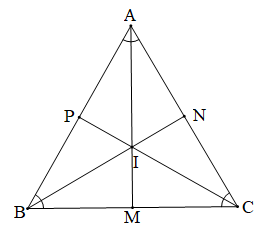
    Giải Toán 7 Bài 13 (Cánh diều): Tính chất ba đường cao của tam giác (ảnh 1) 

    Kéo dài AI cắt BC tại M, kéo dài BI cắt AC tại N, kéo dài CP cắt AB tại P.

    Khi đó AM là đường phân giác của ^BAC nên ^BAM=^CAM;

    Do tam giác ABC đều nên AB = BC = CA.

    Xét ∆ABM và ∆ACM có:

    AB = AC (chứng minh trên),

    ^BAM=^CAM (chứng minh trên),

    AM là cạnh chung

    Do đó ∆ABM = ∆ACM  (c.g.c).

    Suy ra:

    • ^AMB=^AMC (hai góc tương ứng);

    • BM = CM (hai cạnh tương ứng).

    Vì BM = CM nên M là trung điểm của BC.

    Ta có ^AMB=^AMC, mà ^AMB+^AMC=180° nên AMB^=AMC^=180°2=90°.

    Khi đó AM ⊥ BC tại trung điểm M của BC nên AM là đường trung trực của đoạn thẳng BC cũng đồng thời là đường cao và đường trung tuyến kẻ từ A của ∆ABC.

    Chứng minh tương tự ta cũng có:

    +) BN là đường trung trực của đoạn thẳng AC, đồng thời là đường cao và đường trung tuyến kẻ từ B của ∆ABC.

    +) CP là đường trung trực của đoạn thẳng AB, đồng thời là đường cao và đường trung tuyến kẻ từ C của ∆ABC.

    Mà AM, BN, CP cắt nhau tại I nên G, H, I, O trùng nhau.

    b)

    GT

    ∆ABC,

    H là trực tâm,

    I là giao điểm của ba đường phân giác,

    I ≡ H

    KL

    ∆ABC đều

    Chứng minh (Hình vẽ dưới đây):

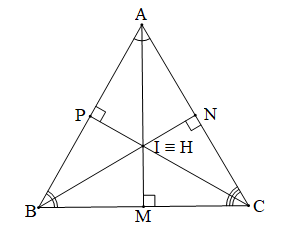
    Giải Toán 7 Bài 13 (Cánh diều): Tính chất ba đường cao của tam giác (ảnh 1) 

    Vì I là giao điểm ba đường phân giác, H là trực tâm của tam giác ABC (giả thiết) nên:

    + AI là đường phân giác và AH là đường cao kẻ từ A của ∆ABC.

    Mà I ≡ H (giả thiết) nên đường phân giác AI trùng với đường cao AH.

    + Tương tự đường phân giác BI trùng đường cao BH;

    + Đường phân giác CI trùng đường cao CH.

    Gọi M, N, P lần lượt là chân đường cao (hay cũng chính là đường phân giác) kẻ từ A, B, C đến BC, CA, AB.

    Xét ∆ABM (vuông tại M) và ∆ACM (vuông tại M) có:

    BAM^=CAM^ (do AM là tia phân giác của BAC^),

    AM là cạnh chung

    Do đó ∆ABM = ∆ACM (cạnh góc vuông – góc nhọn kề).

    Suy ra AB = AC (hai cạnh tương ứng). (1)

    Xét ∆ABN (vuông tại N) và ∆CBN (vuông tại N) có:

    BN là cạnh chung,

    ABN^=CBN^ (do BN là tia phân giác của ABC^),

    Do đó ∆ABN = ∆CBN (cạnh góc vuông – góc nhọn kề).

    Suy ra AB = BC (hai cạnh tương ứng). (2)

    Từ (1) và (2) suy ra AB = BC = CA do đó tam giác ABC là tam giác đều.

    Vậy tam giác ABC đều.

    Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Cánh diều hay, chi tiết khác:

    Câu hỏi khởi động trang 116 Toán 7 Tập 2: Cho tam giác ABC. Gọi M, N, P lần lượt là hình chiếu của A, B, C trên các đường thẳng BC, CA, AB...

    Hoạt động 1 trang 116 Toán 7: Cho tam giác ABC (Hình 133). Bằng cách sử dụng ê ke, vẽ hình chiếu M của điểm A trên đường thẳng BC...

    Luyện tập 1 trang 117 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C...

    Hoạt động 2 trang 117 Toán 7 Tập 2: Quan sát ba đường cao AM, BN, CP của tam giác ABC (Hình 137), cho biết ba đường cao...

    Luyện tập 2 trang 117 Toán 7 Tập 2: Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC...

    Luyện tập 3 trang 118 Toán 7 Tập 2: Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều...

    Bài 1 trang 118 Toán 7 Tập 2: Cho tam giác ABC có H là trực tâm, H không trùng với đỉnh nào của tam giác. Nêu một tính chất của cặp đường thẳng...

    Bài 2 trang 118 Toán 7 Tập 2: Cho tam giác ABC. Vẽ trực tâm H của tam giác ABC và nhận xét vị trí của nó trong các trường hợp sau...

    Bài 3 trang 118 Toán 7 Tập 2: Cho tam giác nhọn ABC và điểm D nằm trong tam giác. Chứng minh rằng nếu DA vuông góc với BC...

    Bài 4 trang 118 Toán 7 Tập 2: Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, HCA^=25°. Tính BAC^ và HBA^...

    Bài 5 trang 118 Toán 7 Tập 2: Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD...

    Bài 6 trang 118 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác...

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài tập cuối chương 7

    Chủ đề 3: Dung tích phổi

    Bài 1: Tập hợp Q các số hữu tỉ

    Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

    Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 499 01/03/2023
    Trang trước
    Trang sau  

    Xem thêm các chương trình khác: