Nội dung bài viết

    Xem thêm

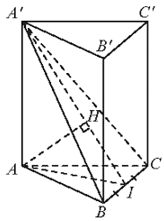
    Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a. Biết d(A;(A'BC'))=(a căn 57)/12

    Lời giải Bài 7 trang 68 SBT Toán 11 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 682 15/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 4: Khoảng cách trong không gian

    Bài 7 trang 68 SBT Toán 11 Tập 2: Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a. Biết d(A(A'BC'))=a5712 . Tính VABC.A'B'C' .

    Lời giải:

    Cho hình lăng trụ đều ABC A'B'C' có cạnh đáy bằng a. Biết

    Gọi I là trung điểm của BC và H là hình chiếu của A trên A'I.

    Ta có: BC ⊥ AI và BC ⊥ AA' ⇒ BC ⊥ (A'AI) ⇒ (A'BC) ⊥ (A'AI).

    Mặt khác (AB'C) ∩ (A'AI) = A'I và AH ⊥ A'I.

    Nên d(A,(A'BC))=AH=a5712

    ∆ABC đều cạnh a ⇒AI=a32 và SABC=a234

    Xét tam giác A'AI vuông tại A, ta có:

    1A'A2=1AH2−1AI2=14457a2−43a2=6857a2⇒AA'=a57217.

    Do đó VABC.A'B'C'=SABC.AA'=a234.a57217=a3171817

    Vậy VABC.A'B'C'=a3171817.

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều canh a, cạnh bên SA...

    Bài 2 trang 68 SBT Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a...

    Bài 3 trang 68 SBT Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' cạnh a.....

    Bài 4 trang 68 SBT Toán 11 Tập 2: Cho hình tứ diện đều ABCD có cạnh bằng 11 ....

    Bài 5 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có tam giác vuông cân tại B...

    Bài 6 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD)...

    Bài 7 trang 68 SBT Toán 11 Tập 2: Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a....

    Bài 8 trang 68 SBT Toán 11 Tập 2: Một hình hộp chữ nhật ABCD.A'B'C'D' có ba kích thước là 2 cm, 3 cm và 6 cm....

    Bài 9 trang 68 SBT Toán 11 Tập 2: Cho hình chóp cụt tam giác đều ABC.A'B'C' có đường cao HH'=2a ....

    Bài 10 trang 68 SBT Toán 11 Tập 2: Tính thể tích một cái sọt đựng đồ có dạng hình chóp cụt tứ giác đều,...

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

    Bài tập cuối chương 8

    Bài 1: Biến cố giao và quy tắc nhân xác suất

    Bài 2: Biến cố hợp và quy tắc cộng xác suất

    Bài tập cuối chương 9

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 682 15/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: