Bài tập tuần Toán lớp 8 Tuần 12 có đáp án chi tiết

Bài tập cuối tuần Toán lớp 8 Tuần 12 chọn lọc, có đáp án và lời giải chi tiết gồm các bài tập từ cơ bản đến nâng cao bám sát nội dung học Tuần 12 Toán lớp 8 giúp học sinh ôn tập để biết cách làm bài tập Toán 8.

1 1,729 28/10/2021

Tải về

Trang trước

Trang sau

Bài tập tuần Toán lớp 8 Tuần 12 có đáp án

Bài 1: Dùng tính chất cơ bản của phân thức, hãy tìm các đa thức trong mỗi đẳng thức sau:

a) $\frac{64 x^{3} + 1}{16 x^{2} - 1} = \frac{A}{4 x - 1}$

b) $\frac{5 x - 2}{B} = \frac{10 x^{2} - 29 x + 10}{10 x^{2} + 27 x - 5}$

c) $\frac{C}{3 x^{2} - 7 x + 4} = \frac{3 - 2 x}{3 x - 4}$

d) $\frac{2 x - y - 1}{4 x - 2 y} = \frac{4 x^{2} - 2 x - y^{2} - y}{D}$

Bài 2: Rút gọn các phân thức

a) $\frac{35 (x^{2} - y^{2}) {(x + y)}^{2}}{77 {(y - x)}^{2} {(x + y)}^{3}}$

b) $\frac{4 x^{2} y^{2} + 1 - 4 x y}{8 x^{3} y^{3} - 1 - 6 x y (2 x y - 1)}$

c) $\frac{x^{2} - x y - x z + y z}{x^{2} + x y - x z - y z}$

d) $\frac{a^{2} + b^{2} - c^{2} + 2 a b}{a^{2} - b^{2} + c^{2} + 2 a c}$

e) $\frac{(x^{2} + 3 x + 2) (x^{2} - 25)}{x^{2} + 7 x + 10}$

f) $\frac{x^{6} - y^{6}}{x^{4} - y^{4} - x^{3} y + x y^{3}}$

Bài 3: Chứng minh các phân thức sau không phụ thuộc vào biếnx

a) $\frac{- 2 y^{2} - 5 y + 2 x y + 5 x}{y^{3} + x - y - x y^{2}}$

b) $\frac{x^{2} y^{2} + 1 + (x^{2} - y) (1 - y)}{x^{2} y^{2} + 1 + (x^{2} + y) (1 + y)}$

Bài 4: Cho đoạn thẳng AG và điểm D nằm giữa hai điểm A và G. Trên cùng nửa mặt phẳng bờ AG vẽ các hình vuông $A B C D, D E F G .$ Gọi M,N lần lượt là trung điểm của $A G, E C .$ Gọi I;K lần lượt là tâm đối xứng của các hình vuông $A B C D, D E F G$

a) Chứng minh: $A E = C G$ và $A E ⊥ C G$ tại H.

b) Chứng minh $I M K N$ là hình vuông.

c) Chứng minh $B, H, F$ thẳng hàng

d) Gọi T là giao điểm của BF và EG. Chứng minh rằng độ dài TM không đổi khi D di động trên đoạn AG cố định.

PHẦN HƯỚNG DẪN GIẢI

Bài 1:

a) Ta có:

$\frac{64 x^{3} + 1}{16 x^{2} - 1} = \frac{{(4 x)}^{3} + 1^{3}}{(4 x - 1) (4 x + 1)} = \frac{(4 x + 1) (16 x^{2} - 4 x + 1)}{(4 x - 1) (4 x + 1)} = \frac{(16 x^{2} - 4 x + 1)}{(4 x - 1)} = \frac{A}{(4 x - 1)}$

Vậy $A = (16 x^{2} - 4 x + 1)$

b) Ta có:

$(- 10 x^{2} + 27 x - 5) (5 x - 2) = - 50 x^{3} + 135 x^{2} - 25 x + 20 x^{2} - 54 x + 10 = - 50 x^{3} + 155 x^{2} - 79 x + 10 = - 5 x (10 x^{2} - 29 x + 10) = B . (10 x^{2} - 29 x + 10)$

Vậy $B = - 5 x$

c) Ta có:

$(3 x^{2} - 7 x + 4) (3 - 2 x) = 9 x^{2} - 21 x + 12 - 6 x^{3} + 14 x^{2} - 8 x = - 6 x^{3} + 23 x^{2} - 29 x + 12 = (3 x - 4) (- 2 x^{2} + 5 x - 3) = (3 x - 4) . C$

Vậy $C = - 2 x^{2} + 5 x - 3$

d) Ta có:

$\frac{2 x - y - 1}{2 (2 x - y)} = \frac{[(2 x - y) (2 x + y) - (2 x + y)]}{D} \frac{2 x - y - 1}{2 (2 x - y)} = \frac{(2 x + y) (2 x - y - 1)}{D} D = 2 (4 x^{2} - y^{2})$

Bài 2:

$\frac{35 (x^{2} - y^{2}) {(x + y)}^{2}}{77 {(y - x)}^{2} {(x + y)}^{3}} = \frac{5.7 (x - y) {(x + y)}^{3}}{7.11 {(y - x)}^{2} {(x + y)}^{3}} = \frac{- 5 (y - x)}{11 {(y - x)}^{2}} = \frac{- 5}{11 (y - x)}$

$\frac{4 x^{2} y^{2} + 1 - 4 x y}{8 x^{3} y^{3} - 1 - 6 x y (2 x y - 1)} = \frac{{(2 x y - 1)}^{2}}{(2 x y - 1) (4 x^{2} y^{2} + 2 x y + 1) - 6 x y (2 x y - 1)} = \frac{{(2 x y - 1)}^{2}}{(2 x y - 1) (4 x^{2} y^{2} - 4 x y + 1)} = \frac{1}{2 x y - 1}$

$\frac{x^{2} - x y - x z + y z}{x^{2} + x y - x z - y z} = \frac{x (x - y) - z (x - y)}{x (x + y) - z (x + y)} = \frac{(x - z) (x - y)}{(x - z) (x + y)} = \frac{x - y}{x + y}$

$\frac{a^{2} + b^{2} - c^{2} + 2 a b}{a^{2} - b^{2} + c^{2} + 2 a c} = \frac{{(a + b)}^{2} - c^{2}}{{(a + c)}^{2} - b^{2}} = \frac{(a + b + c) (a + b - c)}{(a + b + c) (a - b + c)} = \frac{a + b - c}{a - b + c}$

Bài 3:

$\frac{- 2 y^{2} - 5 y + 2 x y + 5 x}{y^{3} + x - y - x y^{2}} = \frac{2 y (x - y) + 5 (x - y)}{- y^{2} (x - y) + (x - y)} = \frac{(x - y) (2 y + 5)}{(x - y) (1 - y^{2})} = \frac{2 y + 5}{1 - y^{2}}$

Vậy phân thức đã cho không phụ thuộc vào biến x.

$\frac{x^{2} y^{2} + 1 + (x^{2} - y) (1 - y)}{x^{2} y^{2} + 1 + (x^{2} + y) (1 + y)} = \frac{x^{2} y^{2} + 1 + x^{2} - x^{2} y - y + y^{2}}{x^{2} y^{2} + 1 + x^{2} + x^{2} y + y + y^{2}} = \frac{x^{2} (y^{2} + 1) + (y^{2} + 1) - y (x^{2} + 1)}{x^{2} (y^{2} + 1) + (y^{2} + 1) + y (x^{2} + 1)} = \frac{(y^{2} + 1) (x^{2} + 1) - y (x^{2} + 1)}{(y^{2} + 1) (x^{2} + 1) + y (x^{2} + 1)} = \frac{(x^{2} + 1) (y^{2} - y + 1)}{(x^{2} + 1) (y^{2} + y + 1)} = \frac{y^{2} - y + 1}{y^{2} + y + 1}$

Vậy phân thức đã cho không phụ thuộc vào biến x

Bài 4:

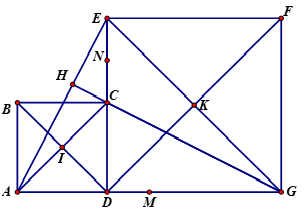
Ta có tứ giác $A B C D, D E F G$ là các hình vuông (gt)

$\Rightarrow \{\begin{cases} \begin{array}{l} A B = B C = C D = A D; \\ \hat{A} = \hat{B} = \hat{C} = \hat{D} \end{array} \\ \begin{array}{l} D E = E F = F G = D G; \\ \hat{D} = \hat{E} = \hat{F} = \hat{G} \end{array} \end{cases}$

Xét $Δ A D E$ và $Δ C D G$ có:

$\begin{array}{l} \begin{array}{l} A D = C D (cmt) \\ \hat{A D E} = \hat{C D G} = 90 ° \end{array}\} \\ \Rightarrow Δ A D E = Δ C D G (c . g . c) \end{array}$

$E D = D G$ (cmt)

$\Rightarrow A E = C G$ (Hai cạnh tương ứng) và $\hat{A E D} = \hat{C G D}$ (Hai góc tương ứng) hay $\hat{H E C} = \hat{C G D}$

Ta có: $\hat{H C E} = \hat{D C G}$ ( Hai góc đối đỉnh)

Mà $\hat{C G D} + \hat{D C G} = 90 °$ (Hai góc phụ nhau)

$\Rightarrow \hat{H C E} + \hat{H E C} = 90 °$

Xét $Δ H E C$ có: $\hat{H C E} + \hat{H E C} = 90 °$ (cmt) $\Rightarrow \hat{E H C} = 90 °$ hay $A E ⊥ C G = {H}$

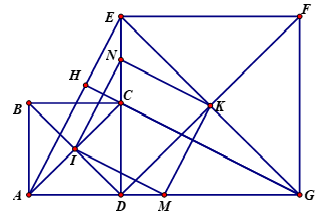
Tài liệu VietJack

Xét $Δ A E C$ có: I là trung điểm của $A C, N$ là trung điểm của EC

IN là đường trung bình của $Δ A E C$

$\Rightarrow I N // A E; I N = \frac{A E}{2}$

Xét $△ A E G$ có: K là trung điểm của $E G, M$ là trung điểm của AG.

KM là đường trung bình của $Δ A E G$ (ĐN)

$\Rightarrow K M // A E; K M = \frac{A E}{2}$

Xét tứ giác $M I N K$ có:

$I N = K M (= \frac{A E}{2})\}$

$\Rightarrow$ Tứ giác $M I N K$ là hình bình hành (DHNB)

$I N // K M (// A E)$

Tương tự ta cũng chứng minh được IM là đường trung bình của $Δ A C G$

$\Rightarrow I M // C G; I M = \frac{C G}{2}$ mà $K M = \frac{A E}{2}$ và $A E = C G$ (cmt)

$\Rightarrow I M = K M$ mà tứ giác $M I N K$ là hình bình hành

Do đó tứ giác $M I N K$ là hình thoi.

Ta có $I M // C G \Rightarrow \hat{I M A} = \hat{A G C}$ (Hai góc đồng vị)

$K M // A E$ (cmt) $\Rightarrow \hat{K M G} = \hat{E A D}$ (Hai góc đồng vị)

Mà $\hat{D C G} = \hat{E A D} (Δ A D E = Δ C D G)$

Nên $\hat{D C G} = \hat{K M G}$

Mà $\hat{A G C} + \hat{D C G} = 90 °$

$\Rightarrow \hat{I M A} + \hat{K M G} = 90 ° \Rightarrow \hat{I M K} = 90 °$

Mà tứ giác $M I N K$ là hình thoi (cmt)

Vậy tứ giác $M I N K$ là hình vuông (đpcm)

C2. Sau khi chứng minh $M I N K$ là hình thoi ta có $I M // C G, C G ⊥ A E$ suy ra $I M ⊥ A E$ mà $A E // I N$ suy ra $I M ⊥ I N$ hay $\hat{N I M} = 90 °$

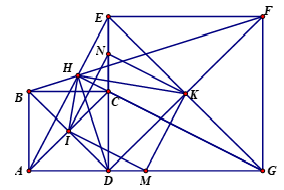
Tài liệu VietJack

Nối $I H, H K$

Ta có $A E ⊥ C G = {H}$ (cmt)

$\Rightarrow \hat{E H G} = \hat{A H C} = 90 °$

Xét $Δ E H G$ có: $\hat{E H G} = 90 °$ và K là trung điểm của EG (Tứ giác DÈG là hình vuông)

Do đó HK là đường trung tuyến ứng với cạnh huyền EG.

$\Rightarrow H K = \frac{E G}{2}$ (tính chất) mà $E G = D F$ ( Tứ giác $D E F G$ là hình vuông)

$\Rightarrow H K = \frac{D F}{2}$

Xét $Δ D H F$ có: $H K = \frac{D F}{2}$ (cmt) $\Rightarrow Δ D H F$ vuông tại $D \Rightarrow \hat{D H F} = 90 °$

Tương tự ta cũng chứng minh được: $I H = \frac{A C}{2}$ mà $A C = B D \Rightarrow I H = \frac{B D}{2}$

$\Rightarrow Δ B H D$ vuông tại H (tính chất) $\Rightarrow \hat{B H D} = 90 °$

Do đó:

$\hat{B H D} + \hat{D H F} = 90 ° + 90 ° = 180 °$

Vậy $B, H, F$ thẳng hàng.

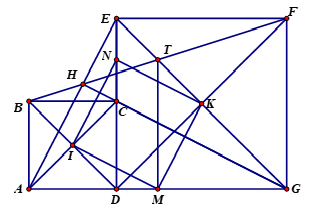
Tài liệu VietJack

Ta có tứ giác $A B C D, D E F G$ là hình vuông (gt) $\Rightarrow \hat{D E G} = \hat{B D E} = 45 °$

Mà hai góc này ở vị trí so le trong $\Rightarrow E G // B D$

Xét: $Δ B D F$ có K là trung điểm của DF mà $E G // B D$ (cmt) hay $T K // B D$

T là trung điểm của BF.

Ta có:

$\hat{B A D} = \hat{F G D} = 90 ° \Rightarrow A B ⊥ A G; F G ⊥ A G \Rightarrow A B // F G$

Tứ giác $A B F G$ là hình thang

Ta có: T là trung điểm của BF (cmt), M là trung điểm của AG (gt)

TM là đường trung bình của hình thang ABFG

$\Rightarrow T M = \frac{A B + F G}{2} = \frac{A D + D G}{2} = \frac{A G}{2}$

Mà AG không đổi nên độ dài TM không đổi khi D di động trên đoạn AG cố định.

1 1,729 28/10/2021

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3