Nội dung bài viết

    Xem thêm

    Bài tập tuần Toán lớp 8 Tuần 3 có đáp án chi tiết

    Bài tập cuối tuần Toán lớp 8 Tuần 3 chọn lọc, có đáp án và lời giải chi tiết gồm các bài tập từ cơ bản đến nâng cao bám sát nội dung học Tuần 3 Toán lớp 8 giúp học sinh ôn tập để biết cách làm bài tập Toán 8.

    1 3,558 26/10/2021
    Tải về
    Trang trước
    Trang sau  

    Bài tập tuần Toán lớp 8 Tuần 3 có đáp án

    Bài 1: Viết các biểu thức sau dưới dạng một tích các đa thức:

    a) 16x2−9

    b) 9a2−25b4

    c) 81−y4

    d) (2x+y)2−1

    e) (x+y+z)2−(x−y−z)2

    Bài 2: Dùng hằng đẳng thức để khai triển và thu gọn:

    a) (2x2+13)3

    b) (2x2y−3xy)3

    c) (−3xy4+12x2y2)3

    d) (−13ab2−2a3b)3

    e) (x+1)3−(x−1)3−6(x−1)(x+1)

    f)

    x(x−1).(x+1)−(x+1).(x2−x+1)

    g)

    (x−1)3−(x+2)(x2−2x+4)+3(x−4)(x+4)

    h)

    3x2(x+1)(x−1)+(x2−1)3−(x2−1)(x4+x2+1)

    k)

    (x4−3x2+9)(x2+3)+(3−x2)3−9x2(x2−3)

    l) (4x+6y).(4x2−6xy+9y2)−54y3

    Bài 3: Tứ giác ABCD có AB//CD, AB < CD, AD = BC. Chứng minh ABCD là hình thang cân.

    Bài 4: Cho ΔABC có AB < AC, AH là đường cao. Gọi M,N,K lần lượt là trung điểm của  AB,AC,BC

    a) Chứng minh MNKH là hình thang cân.

    b) Trên tia AH và AK lần lượt lấy điểm E và D sao cho H là trung điểm của AE và K là trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân.

    PHẦN HƯỚNG DẪN GIẢI

    Bài 1      

    a)

    16x2−9=(4x)2−32(4x+3)(4x−3)

    b)

    9a2−25b4=(3a)2−(5b2)2=(3a+5b2)(3a+5b2)

    c)

    81−y4=92−(y2)2=(9+y2)(9−y2)

    d)

    (2x+y)2−1=(2x+y)2−12=(2x+y+1)(2x+y−1)

    e)

    (x+y+z)2−(x−y−z)2=(x+y+z+x−y−z)(x+y+z−x+y+z)=2x.(2y+2z)=4x.(y+z)

    Bài 2:

    a)

    (2x2+13)3=(2x2)3+3.(2x2)2.13+3.2x2.(13)2+(13)3=8x6+4x4+23x2+127

    b) (2x2y−3xy)3

    =(2x2y)3−3.(2x2y)2.3xy+3.2x2y.(3xy)2−(3xy)3=8x6y3−36x5y3+54x4y3−27x3y3

    c)  

    (−3xy4+12x2y2)3=(12x2y2−3xy4)3

    =(12x2y2)3−3.(12x2y2)2.3xy4+3.12x2y2.(3xy4)2−(3xy4)3=18x6y6−94x5y8+272x4y10−27x3y12

    d)  

    (−13ab2−2a3b)3=−(13ab2+2a3b)3

    =−[(13ab2)3+3.(13ab2)2.2a3b+3.13ab2.(2a3b)2+(2a3b)3]=−(127a3b6+23a5b5+4a7b4+8a9b3)=−127a3b6−23a5b5−4a7b4−8a9b3

    e)

    (x+1)3−(x−1)3−6(x−1)(x+1)=x3+3x2+3x+1−(x3−3x2+3x−1)−6(x2−1)=x3+3x2+3x+1−x3+3x2−3x+1−6x2+6=6x2+2−6x2+6=8

    f)

    x(x−1).(x+1)−(x+1).(x2−x+1)=x(x2−1)−(x3+1)=x3−x−x3−1=−x−1 

    g)

    (x−1)3−(x+2)(x2−2x+4)+3(x−4)(x+4)=x3−3x2+3x−1−(x3+8)+3(x2−16)=x3−3x2+3x−1−x3−8+3x2−48=3x−57=3(x−19)

    h)

    3x2(x+1)(x−1)+(x2−1)3−(x2−1)(x4+x2+1)=3x2(x2−1)+(x2)3−3(x2)2+3x2−1−(x3−1)=3x4−3x2+x6−3x4+3x2−1−x3+1=x6−x3

    k)

    (x4−3x2+9)(x2+3)+(3−x2)3−9x2(x2−3)=(x2)3+27+27−3.9.x2+3.3.(x2)2+( 

    l)

    4x+6y.4x2−6xy+9y2−54y3=2.2x+3y.4x2−6xy+9y2−54y3=2.2x3+3y3−54y3=16x3+54y3−54y3=16x3

    Bài 3: 

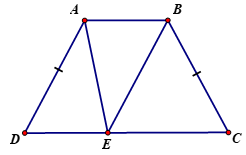
    Tài liệu VietJack

    Từ B kẻ BE//ADE∈BC

    Vì AB < CD nên điểm E nằm giữa C và D.

    Tứ giác ABED là hình thang có

    AB//CD( giả thiết) và BE//AD (cách dựng) nên AD = BE

    Mà AD = BC (giả thiết)⇒BE = BC⇒ΔBEC cân tại B (dấu hiệu nhận biết)

    ⇒BEC^=C^

    Mà  BE//AD nên D^=BEC^ (đồng vị)

    ⇒D^=C^ mà tứ giác ABCD là hình thang (dấu hiệu nhận biết)

    Vậy tứ giác ABCD là hình thang cân

    Bài 4:

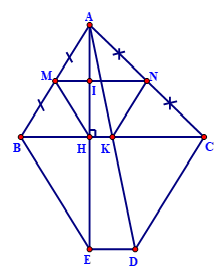
    Tài liệu VietJack

    a) Chứng minh MNKH là hình thang cân.

    Do MA = MB (gt), NA = NC (gt), KB = KC (gt)

    MN,NK là các đường trung bình của ΔABC

    ⇒MN // BCNK // AB(tính chất đường TB)

    ⇒MN // HKANM^=MNK^

    Do MN//BC hay MI//BH mà  MA = MB

    IA = IH (với I là giao của MN và AH)

    Lại có :

    AH⊥BC⇒AH⊥MN

    Suy ra MN là đường trung trực của AH

    ⇒AM=MH⇒ΔMAH

    cân tại  M

    MN là phân giác của AMH^ (tính chất tam giác cân)

    ⇒AMN^=NMH^

    Mà ANM^=MNK^ (cmt)

    ⇒NMH^=MNK^

    Xét tứ giác MNKH có: MN//HK và NMH^=MNK^

    ⇒MNKH là hình thang cân.

    b) Trên tia AH và AK lần lượt lấy điểm E và D sao cho H là trung điểm của AE và K là  trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân.

    Do AH = HE (gt), AK = KD (gt) HK là đường trung bình của tam giác AED

    ⇒HK//ED hay BC//ED (tính chất đường trung bình)

    Lại có NA = NC (gt), KA= KD (gt) Suy ra Nk là đường trung bình của tam giác ACD

    ⇒NK//CD⇒ABH^=BCD^(1)  (so le trong)

    Dễ thấy tam giác ABE cân tại B vì BH vừa là đường cao vừa là trung tuyến

    BH  là phân giác của ABE^⇒ABH^=HBE^ (2)

    Từ (1), (2) ⇒HBE^=BCD^ hay ⇒CBE^=BCD^

    Xét tứ giác BCDE có BC//ED và CBE^=BCD^⇒ tứ giác BCDE là hình thang cân.

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 3,558 26/10/2021
    Tải về
    Trang trước
    Trang sau  

    Xem thêm các chương trình khác: