Nội dung bài viết

    Xem thêm

    Bài tập tuần Toán lớp 8 Tuần 4 có đáp án chi tiết

    Bài tập cuối tuần Toán lớp 8 Tuần 4 chọn lọc, có đáp án và lời giải chi tiết gồm các bài tập từ cơ bản đến nâng cao bám sát nội dung học Tuần 4 Toán lớp 8 giúp học sinh ôn tập để biết cách làm bài tập Toán 8.

    1 4,465 28/10/2021
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Bài tập tuần Toán lớp 8 Tuần 4 có đáp án

    Bài 1: Biến đổi các biểu thức sau thành tích các đa thức:

    a) x3+8

    b) 27−8y3

    c) y6+1

    d) 64x3−18y3

    e) 125x6−27y9

    f) −x6125−y364

    Bài 2: Điền hàng tử thích hợp vào chỗ có dấu * để có hằng đẳng thức:

    a) x2+4x+*=*+*2

    b) 9x2−*+4=*−*2

    c) x2+x+*=*+*2

    d) *−2a+4=*−*2

    e) 4y2−*=*−3x*+*

    f) *−14=3y−**+*

    g) 8x3+*=*+2a4x2−*+*

    h) *−27x3=4x−*9y2+*+*

    Bài 3: Tìm  biết:

    a) x2−2x+1=25

    b) 5x+12−5x−35x+3=30

    c)

    x−1x2+x+1−xx+2x−2=5

    d)

    x−23−x−3x2+3x+9+6x+12=15

    Bài 4: Cho ΔABC và đường thẳng d qua A không cắt đoạn thẳng BC. Vẽ  BD⊥d,CE⊥d, D,E∈d. Gọi I là trung điểm của BC. Chứng minh ID = IE.

    Bài 5: Cho hình thang ABCD có AB song song với CD ( AB < CD) và M là trung điểm của AD . Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E,F.  Chứng minh rằng N,E,F lần lượt là trung điểm của  BC,BD,AC.

    PHẦN HƯỚNG DẪN GIẢI

    Bài 1:     

    a)

    x3+8=x3+23=x+2x2−2x+4

    b)

    27−8y3=33−2y3=3−2y9+6y+4y2

    c)

    y6+1=y23+1=y2+1y4−y2+1

    d)

    64x3−18y3=4x3−12y3=4x−12y16x2+2xy+14y2

    e)

    125x6−27y9=5x23−3y33=5x2−3y35x22+5x2.3y3+3y32=5x2−3y325x4+15x2y3+9y6

    f)

    −x6125−y364=−x6125+y364=−x253+y43=−x25+y4x252−x25.y4+y42=−x25+y4x425−x2y20+y216

    Bài 2:

    a)

    x2+4x+*=*+*2⇔x2+2.x.2+22=x+22

    b)

    9x2−*+4=*−*2⇔3x2−2.3x.2+22=9x2−12x+22=3x−22

    c)

    x2+x+*=*+*2⇔x2+2.x.12+122=x+122

    d)

    *−2a+4=*−*2⇔a22−2.a2.2+22=a2−22

    e)

    4y2−*=*−3x*+*⇔2y2−3x2=2y−3x2y+3x  

    f)

    *−14=3y−**+*=3y2−122=3y+123y−12

    g)

    8x3+*=*+2a4x2−*+*⇔2x3+2a3=2x+2a4x2−2x.2a+4a2

    h)

    *−27x3=4x−*9y2+*+*⇔4x3−3y3=4x−3y16x2+12xy+9y2

    Bài 3: 

    a)

    x2−2x+1=25x−12=±52x−1=±5

    x−1=5 hoặc x−1=−5

    x=6 hoặc x=-4

    Kết luận: Vậy x=6 hoặc x=-4 là giá trị cần tìm.

    b)

    5x+12−5x−35x+3=3025x2+10x+1−25x2+9=3010x=30−1010x=20   x=2

    Kết luận: Vậy x=2 là giá trị cần tìm.

    c)

    x−1x2+x+1−xx+2x−2=5x3−1−xx2−4=5x3−1−x3+4x=54x=6   x=32

    Kết luận: vậy x=32 là giá trị cần tìm

    d)

    x−23−x−3x2+3x+9+6x+12=15x3−6x2+12x−8−x3+27+6x2+2x+1=15−6x2+12x+19+6x2+12x+6=1524x=15−2524x=−10   x=−512

    Kết luận: vậy x= 512 là giá trị cần tìm

    Bài 4: Chứng minh ID = IE.

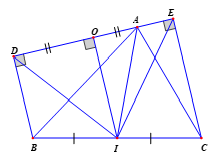
    Tài liệu VietJack

    Ta có: BD // CE  (vì cùng vuông góc với d) nên tứ giác BDEC là hình thang.

    Gọi O là trung điểm của ED

    Khi đó,  OIlà đường trung bình của hình thang BDEC

    ⇒OI//BD//CE;OI=BD+CE2

    Vì  BD⊥d;  CE⊥d nên OI⊥d

    ΔIDE có IO vừa là đường cao, vừa là đường trung tuyến nên ΔIDE cân tại I hay  ID=IE

    Bài 5: 

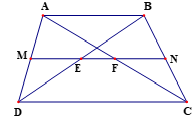
    Tài liệu VietJack

    a) Chứng minh rằng N, E, F  lần lượt là trung điểm của BC, BD, AC

    - Xét hình thang ABCD có:

    M là trung điểm AD(gt)

    N∈BC,MN//AB,MN//CD  (gt)

    N là trung điểm của BC (định lý đường trung bình của hình thang)

    - Xét ΔABD có:

    M là trung điểm AD  (gt),E∈BD

    ME//AB (vì MN//AB,E∈MN)

    E là trung điểm của BD ( định lý đường trung bình của tam giác)

    - Xét ΔACD có:

    M là trung điểm AD  (gt),F∈AC

    MF//CD (vì MN//CD,F∈MN)

    F là trung điểm của AC (định lý đường trung bình của tam giác)

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 4,465 28/10/2021
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: