Nội dung bài viết

    Xem thêm

    Bài tập tuần Toán lớp 8 Tuần 10 có đáp án chi tiết

    Bài tập cuối tuần Toán lớp 8 Tuần 10 chọn lọc, có đáp án và lời giải chi tiết gồm các bài tập từ cơ bản đến nâng cao bám sát nội dung học Tuần 10 Toán lớp 8 giúp học sinh ôn tập để biết cách làm bài tập Toán 8.

    1 2,149 28/10/2021
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Bài tập tuần Toán lớp 8 Tuần 10 có đáp án

    Bài 1: Tìm x:

    a)

    12x4−6x3−9x2:−3x2−2−3x2+3x=−3x+1

    b)

    6x3−x2−26x+21:2x−3−3x−2x+2=−8

    Bài 2: Cho fx=x4−9x3+21x2+x+a;  g(x)=x2−x−2;hx=x3+bx2+cx−5;k(x)=x2+x+1 . Tìm a,  b,  c,  d để

    a) f(x)⋮g(x),∀x

    b) h(x)⋮k(x),∀x.

    Bài 3: Phân tích thành nhân tử:

    a) 9x2−30xy+25y2

    b) 27a9−125b6

    c) 8x3−64y6

    d) x9−64x3

    e) 4x8−4x2y6

    f) x(xa−xb)2+125(b−a)2

    g) (b−a)(a+3b)+(a−b)(a+b)+(b−a)2

    h) (2−x)2+(x−2)(x+3)−4x2−1

    i)(a−b)2(2a−3b)−(b−a)2(3a−5b)+(a+b)2(a−2b)

    j) x4−4x2+5−25

    Bài 4:  Cho tứ giác ABCD có AB⊥CD. Gọi M, N, P, Q lần lượt là trung điểm của BC,BD,AD,AC. Chứng minh rằng :

    a) Tứ giác MNPQ là hình chữ nhật.

    b) Biết BC // AD, BC=4cm, AD=16cm. Tính MP.

    Bài 5:  Cho hình chữ nhật ABCD. Tia phân giác góc  A^ cắt tia phân giác góc D^  tại M, tia phân giác góc B^ cắt tia phân giác góc C^ tại N. Gọi  E,F lần lượt là giao điểm của  DM,CN với AB. Chứng minh rằng:

    a)  AM=DM=BN=CN=ME=NF.

    b) Tứ giác DMNC là hình thang cân.

    c)  AF=BE.

    d) AC, BD, MN đồng quy

    Bài 6:   Cho ABC = 90° có AB<AC. Gọi M là trung điểm của BC.  Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E. Vẽ đường cao AH của ΔABC.

    a) Chứng minh ADME là hình chữ nhật.

    b) Chứng minh CMDE là hình bình hành.

    c) Chứng minh MHDE là hình thang cân.

    d) Qua A kẻ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.

    PHẦN HƯỚNG DẪN GIẢI

    Bài 1:  

    a)

    12x4−6x3−9x2:−3x2−2−3x2+3x=−3x+1⇔−4x2+2x+3−4−9x2=−3x+1⇔5x2+5x=0⇔5x(x+1)=0⇔x=0x=−1

    b)

    6x3−x2−26x+21:2x−3−3x−2x+2=−8⇔6x3−9x2+8x2−12x+−14x+21:2x−3−3x2−4=−8⇔3x22x−3+4x2x−3−72x−3:2x−3−3x2−4=−8⇔3x2+4x−7−3x2−4=−8⇔4x+5=−8⇔x=−134

    Bài 2:

    a) Thực hiện phép chia fx cho gx :

    −x4−9x3+21x2+x+a           x4−   x3−  2x2                               ¯x2−x−2x2−8x+15                  −−8x3+23x2+x+a−8x3+8x2+16x       ¯                              −15x2−15x+a15x2−15x−30¯                                                        a+30

    Thương x2−8x+15 , phép chia có dư a+30 .

    Để fx⋮gx, ∀x

    ⇔a+30=0⇔a=−30

    b) Thực hiện phép chia hx cho  kx:

    −x3+bx2+cx−5                        x3+x2   +x                                   ¯x2+x+1x+b+1−b−1x2+c−1x         −5b−1x2+b−1x+b−1¯                            c−bx−b−4

    Thương x+b+1 , phép chia có dư c−bx−b−4.

    Để hx⋮kx,∀x

    ⇔c−b=0−b−4=0⇔c=b=−4

    Bài 3:

    a)

    9x2−30xy+25y2=3x−5y2

    b)

    27a9−125b6=3a33−5b23=3a3−5b29a6+15a3b2+25b4

    c)

    8x3−64y6=(2x)3−4y23=2x−4y24x2+8xy2+16y4

    d)

    x9−64x3=x33−4x3=x3−4xx6+4x4+16x2

    e)

    4x8−4x2y6=4x2x6−y6=4x2x2−y2x4+x2y2+y4=4x2(x−y)(x+y)x4+x2y2+y4

    f)

    xxa−xb2+125b−a2=x−xb−a2+125b−a2=x3b−a2+125b−a2=b−a2x3+125=b−ab−ax+5x2−5x+25

    g)

    b−aa+3b+a−ba+b+b−a2=b−aa+3b−b−aa+b+b−a2=b−aa+3b−a−b+b−a=b−a3b−a

    h)

    2−x2+x−2x+3−4x2−1=2−x2−2−xx+3−4x2−1=2−x2−x−x−3−4x2−1=−2−x2x+1−2x+12x−1=−2x+12−x+2x−1=−2x+1x+1

    i)

    a−b22a−3b−b−a23a−5b+a+b2a−2b=a−b22a−3b−3a+5b+a+b2(a−2b)=a−b22b−a−a+b22b−a=2b−aa−b2−a+b2=2b−a−2b2a=−4ab2b−a

    j)

    x4−4x2+5−25=x4−25−4x2+5=x2+5x2−5−4=x2+5x2−9=x2+5x−3x+3

    Bài 4:

    Lời giải:

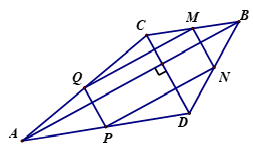
    Tài liệu VietJack

    a) Trong tam giác ACD, PQ là đường trung bình, suy ra  PQ // CD.

    Tương tự, MN // CD, MQ // AB, NP // AB.

    Từ đó ta có MN // PQ và  NP // MQ

    Suy ra MNPQ là hình bình hành.

    Mặt khác, AB⊥CD⇒MN⊥MQ.

    Vậy MNPQ là hình chữ nhật.

    b) Ta có MP=NQ. Theo giả thiết thì BCAD là hình thang với hai đáy BC,AD và QN là đường trung bình nên :

    MP=NQ=12BC+AD=10cm.

    Bài 5:

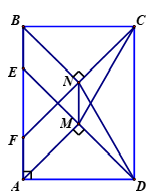
    Tài liệu VietJack

    a) Dễ thấy các tam giác ADM, BCN, AME, BNF là các tam giác vuông cân với các đỉnh lần lượt là  M,N

    do đó AM=DM=EM và BN=CN=FN.

    Mặt khác, vì AD=BC nên ΔAMD=ΔCNB.

    ⇒AM=BN

    Vậy:

    AM=DM=EM=BN=CN=FN.

    b) Tam giác ADE vuông tại A có :

    ADE=45°⇒AED^=45°.

    Lại có ABN^=45°, do đó BN // EM.

    Theo trên BN=EM, do vậy BNME là hình bình hành, suy ra  MN//BE//CD.

    Mặt khác CN=DM. Vậy CDMN là hình thang cân.

    c) Chứng minh tương tự như trên, ta có AFNM cũng là hình bình hành.

    Từ đó suy ra AF=BE=MN.

    d) Theo chứng minh trên ta có BN // MD và BN=MD, do đó BNDM là hình bình hành, suy ra BD và MN cắt nhau tại trung điểm mỗi đoạn. Mặt khác  BD và AC cũng cắt nhau tại trung điểm mỗi đoạn.

    Vậy AC, BD, MN đồng quy tại trung điểm mỗi đoạn.

    Bài 6:

    a) Tứ giác ADME có:

    A^=D^=E^=90° nên ADME là hình chữ nhật.

    b) MD⊥AB, AC⊥AB, suy ra MD // AC.

    Vì M là trung điểm của BC nên MD là đường trung bình của ΔABC.

    Tương tự, ME cũng là đường trung bình của ΔABC. Từ đó ta có A,E lần lượt là trung điểm của AB, AC.

    Suy ra MD//CE và DE//MC. Vậy CMDE là hình chữ nhật.

    c) Theo trên thì DE//HM   (1).

    Xét tam giác ABH vuông tại H, có HD là trung tuyến nên HD=12AB.

    Mặt khác, trong tam giác ABC,ME là đường trung bình nên ME=12AB.

    Suy ra HD=ME  (2).

    Từ (1) và (2) suy ra MHDE là hình thang cân.

    d) Xét hai tam giác ADK và DBH, có:

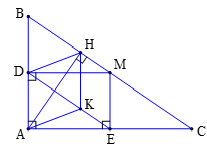
    Tài liệu VietJack

    DE//BC⇒ADK^=DBH^ (Hai góc đồng vị).

    AD=DB (vì D là trung điểm của AB)

    DH//AK⇒DAK^=BDH^(Hai góc đồng vị).

    Suy ra:

    ΔADK=ΔDBH⇒AK=DH

    Lại có AK // DH, do đó ADHK là hình bình hành, suy ra HK // DA. 

    Vì DA⊥AC nên HK⊥AC.

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,149 28/10/2021
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: