Nội dung bài viết

    Xem thêm

    Bài tập tuần Toán lớp 8 Tuần 22 có đáp án chi tiết

    Bài tập cuối tuần Toán lớp 8 Tuần 22 chọn lọc, có đáp án và lời giải chi tiết gồm các bài tập từ cơ bản đến nâng cao bám sát nội dung học Tuần 22 Toán lớp 8 giúp học sinh ôn tập để biết cách làm bài tập Toán 8.

    1 1,977 30/10/2021
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Bài tập tuần Toán lớp 8 Tuần 22 có đáp án

    Bài 1: Giải các phương trình sau

    a) 4x−1−5x−2=−3

    b) 3x−1x−2=x−12−x

    c)

    x+4x2−3x+2+x+1x2−4x+3=2x+5x2−4x+3

    d) 2x2−4−1xx−2+x−4xx+2=0

    e)

    4xx2+4x+3−1=61x+3−12x+2

    f)

    34x−5+1550−2x2=76x+30

    g)

    1x−1+2x2−5x3−1=4x2+x+1

    h)

    12x+16x−2−9x−53x+1=108x−36x2−949x2−1

    i) x+1x=x2+1x2

    j) 1x+2=1x+2x2+2

    Bài 2: Cho ΔABC có AB=6 cm,AC=9 cm,BC=10 cm, đường phân giác trong AD, đường phân giác ngoài AE.

    a) Tính  DB,DC,EB.

    b) Đường phân giác CF của ΔABC cắt AD ở I. Tính tỉ số diện tích ΔDIF và diện tích ΔABC.

    Bài 3: Cho tam giác ABC cân ở A, phân giác trong BD,BC=10 cm,AB=15 cm. Tính AD,DC.

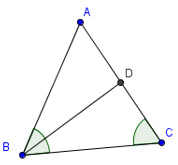
    Bài 4: Cho tam giác ABC có 3 phân giác trong AM,BN,CP cắt nhau tại I. Chứng minh

    a) APAP⋅BMBC⋅CNCA=1

    b) MIMA+NINB+PIPC=1

    PHẦN HƯỚNG DẪN GIẢI

    a) 4x−1−5x−2=−3

    Điêu kiện:

    x−1≠0x−2≠0⇔x≠1x≠2

    Mẫu chung: x−1x−2

    Phương trình (1) trở thành:

    4x−2x−1x−2−5x−1x−2x−1=−3x−1x−2x−1x−2⇒4x−2−5x−1=−3x−1x−2⇔4x−8−5x+5=−3x2−3x+2⇔−x−3=−3x2+9x−6⇔3x2−10x+3=0⇔3x2−9x−x+3=0⇔3xx−3−x−3=0⇔x−33x−1=0⇔x−3=03x−1=0

     ⇔x=3   tmx=13  (L) (nhận)

    Vậy  S=13;3

    b) 3x−1x−2=x−12−x

    Điều kiện: x−2≠0⇔x≠2

    Mẫu chung: x−2

    Phương trình (2) trở thành:

    3xx−2x−2−1x−2=−x−1x−2⇒3xx−2−1=−x−1⇔3x2−6x−1+x−1=0⇔3x2−5x−2=0⇔3x2−6x+x−2=0⇔3xx−2+x−2=0⇔x−23x+1=0⇔x−2=03x+1=0⇔x=2  Lx=−13  tm

    Vậy S=−13

    c)  

    x+4x2−3x+2+x+1x2−4x+3=2x+5x2−4x+3⇔x+4x−1x−2+x+1x−1x−3=2x+5x−1x−3(3)

    Điều kiện :

    x−1≠0x−2≠0x−3≠0⇔x≠1x≠2x≠3

    Phương trình (3) trở thành

    x+4x−3x−1x−2x−3+x+1x−2x−1x−3x−2=2x+5x−2x−1x−3x−2⇒x+4x−3+x+1x−2=2x+5x−2⇔x2+x−12+x2−x−2=2x2+x−10⇔−x=4

    ⇔−x=4 (nhận)

    Vậy S=−4

    d)

    2x2−4−1xx−2+x−4xx+2=0⇔2x−2x+2−1xx−2+x−4xx+2=0(4)

    Điều kiện: x≠0x+2≠0x−2≠0

    ⇔x≠0x≠−2x≠2

    Mẫu chung: xx+2x−2 

    Phương trình (4) trở thành:

    2xx−2x+2x−1x+2xx−2x+2+x−4x−2xx+2x−2=0⇒2x−x+2+x−4x−2=0⇔2x−x−2+x2−6x+8=0⇔x2−5x+6=0⇔x2−2x−3x+6=0⇔x(x−2)−3(x−2)=0⇔(x−2)(x−3)=0⇔x−2=0x−3=0⇔x=2x=3

    Vậy  S=3

    e)

    4xx2+4x+3−1=61x+3−12x+2⇔4x(x+1)(x+3)−1=61x+3−12(x+1)(5)

    Điều kiện: x+1≠0x+3≠0

    ⇔x≠−1x≠−3

    Mẫu chung: 2x+1x+3

    Phương trình (5) trở thành:

    4.2x2x+1x+3−2x+1x+32x+1x+3=61x+1.2x+3x+1.2−1x+32x+1x+3⇒4.2x−2x+1x+3=62x+1−(x+3⇔8x−2x2+4x+3=62x+2−x−3⇔8x−2x2−8x−6=6x−1⇔−2x2−6x=0⇔−2xx+3=0⇔x=0x+3=0⇔x=0(t/m)x=−3(L)

     Vậy S=0

    f)

    34x−5+1550−2x2=76x+30⇔34x−5−152x2−25=76(x+5)⇔34(x−5)−152x−5x+5=76x+5(6)

    Điều kiện:  x+5≠0x−5≠0

    ⇔x≠−5x≠5

    Mẫu chung: 12x+5x−5

    Phương trình (6) trở thành

    3.3x+54.3x+5x−5−15.62x−5x+5=7.2x−56x+5.2x−5⇒9x+5−15.6=14x−5⇔9x+45−90=14x−70⇔−5x=−25

    ⇔x=5 (loại)

    Vậy  S={∅}

    g)  

    1x−1+2x2−5x3−1=4x2+x+1⇔1x−1+2x2−5x−1x2+x+1=4x2+x+1  (7)

    Điều kiện: x−1≠0⇔x≠1

    vì x2+x+1>0∀x

    Mẫu chung:  x−1x2+x+1

    Phương trình (7) trở thành

    1x2+x+1x−1x2+x+1+2x2−5x−1x2+x+1=4x−1x2+x+1x−1⇒x2+x+1+2x2−5=4x−4⇔3x2−3x=0⇔3x(x−1)=0⇔x=0x−1=0⇔x=0  tmx=1   L

    Vậy S={0}

    h)

    12x+16x−2−9x−53x+1=108x−36x2−949x2−1⇔12x+123x−1−9x−53x+1=108x−36x2−943x−13x+1   8

    Điều kiện:  3x−1≠03x+1≠0

    ⇔x≠13x≠−13

    Mẫu chung:  43x+13x−1

    Phương trình (8) trở thành:

    212x+13x+12.23x+13x−1−49x−53x−143x+13x−1=108x−36x2−943x−13x+1⇒212x+13x+1−49x−53x−1)=108x−36x2−9⇔236x2+15x+1−427x2−24x+5−108x+36x2+9=0⇔72x2+30x+2−108x2+96x−20−108x+36x2+9=0⇔18x−9=0

    ⇔x=918⇔x=12 (nhận)

    Vậy  S=12

    i)

    x+1x=x2+1x2⇔x+1x=x+1x2−2x.1x⇔x+1x2−x+1x−2=0

    Điều kiện:  x≠0

    Đặt x+1x=t, phương trình (9) trở thành

    t2−t−2=0⇔t2+t−2t−2=0⇔tt+1−2t+1=0⇔t−2t+1=0⇔t−2=0t+1=0⇔t=2t=−1

    Với t=2, ta có :

    x+1x=2⇒x2+1=2x⇔x2−2x+1=0

    ⇔x−12=0

    ⇔x−1=0⇔x=1 (nhận)

    Với t=−1, ta có :

    x+1x=−1⇒x2+1=−x⇔x2+x+1=0

    ⇔x+122+34=0 (vô nghiệm)

    vì x+122+34>0∀x

    Vậy  S=1

    j) 

    1x+2=1x+2x2+2⇔1x+2−1x+2x2+2=0

    Điều kiện: x≠0 

    ⇔1x+2−1x+2x2+2=0⇔1x+21−x2−2=0⇔1x+2−x2−1=0⇔−1x+2x2+1=0⇔1x+2=0

    Vì x2+1>0∀x⇒1+2x=0

    ⇔x=−12

    Vậy  S=−12

    Bài 2:

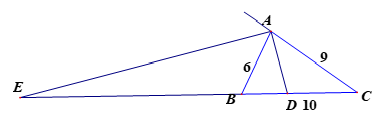
    Tài liệu VietJack

    Ta có:

    BDCD=ABAC=69=23

    (do AD là phân giác trong của ΔABC)

    ⇒BD=23⋅DC

    Mà BD+DC=BC=10 (do D nằm giữa B và C)

    ⇒23DC+DC=10⇒53DC=10⇒DC=6 cm⇒BD=4 cm

    Ta có: CE=BE+BC=BE+10 (do B nằm giữa E và C)

    Và BECE=ABAC=23 (do AE là phân giác ngoài của ΔABC)

    ⇒BEBE+10=23⇒3BE=2BE+10⇒BE=20 cm

    Vậy BD=4 cm,DC=6 cm,BE=20 cm

    Bài 3:

    Tài liệu VietJack

    DA+DCDC=BA+BCBC⇒ACDC=15+1010⇒DC=10.AC25=10.1525=6( cm)

    Ta có:

    DA+DC=AC⇒AD=AC−DC=15−6=9( cm)

    Bài 4:

    a) Ta có AM là phân giác của góc A

    Theo tính chất đường phân giác trong tam giác, ta có

    MBMC=ABAC

    Tương tự đối với các đường phân giác BN,CP ta có:

    NCNA=BCBA;PAPB=CACB

    Do đó:

    MBMC⋅NCNA⋅PAPB=ABAC⋅BCBA⋅CACB=1

    Vậy APAP⋅BMBC⋅CNCA=1

    b) Gọi a,b,c lần lượt là độ dài của các cạnh BC,CA,AB.

    Trong ΔABM thì BI là phân giác ứng với cạnh AM nên

     MIIA=BMBA=BMc⇒MIMI+IA=BMBM+c⇒MIMA=BMBM+c (1)

    Trong ΔACM thì CI là phân giác ứng với cạnh AM nên

    MIIA=CMCA=CMb⇒MIMI+IA=CMCM+b⇒MIMA=CMCM+b

    Mà CM = BC - BN = a - BM.

    Nên  MIMA=a−BMa−BM+b (2)

    So sánh (1) và (2) ta có:

    MIMA=BMBM+c=a−BMa−BM+b=BM+a−BMBM+c+a−BM+b⇒MIMA=aa+b+c

    Chứng minh tương tự ta có:

    NIBN=ba+b+c

    PICP=ca+b+c

    Suy ra:

    MIMA+NIBN+PICP=aa+b+c+ba+b+c+ca+b+c=a+b+ca+b+c=1

    Vậy MIMA+NINB+PIPC=1

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,977 30/10/2021
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: