TOP 31 câu hỏi Trắc nghiệm Bài tập cuối chương 4 có lời giải - Toán lớp 6 Kết nối tri thức

Trắc nghiệm Toán 6 Bài tập cuối chương 4

A. Lý thuyết

1. Hình tam giác đều

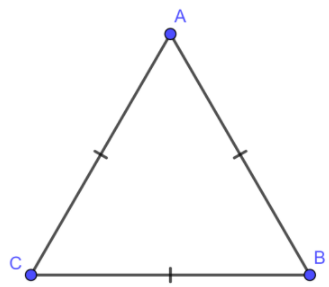
Trong tam giác đều:

- Ba cạnh bằng nhau.

- Ba góc bằng nhau và bằng 60⁰C.

2. Hình vuông

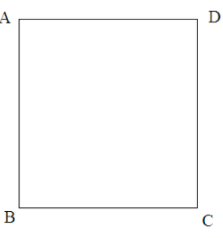
Trong hình vuông:

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng 90⁰.

- Hai đường chéo bằng nhau.

3. Hình lục giác đều

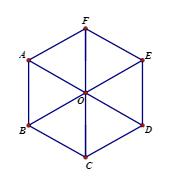
Hình lục giác đều có:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau, mỗi góc bằng 120⁰.

- Ba đường chéo chính bằng nhau.

4. Hình chữ nhật

Trong hình chữ nhật có:

- Bốn góc bằng nhau và bằng 90⁰C.

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

5. Hình thoi

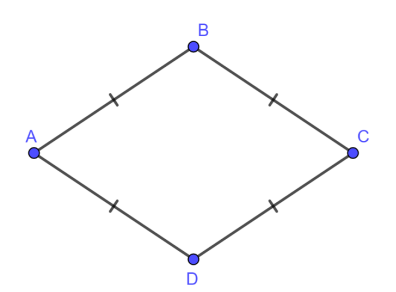
Trong hình thoi :

- Bốn cạnh bằng nhau.

- Hai đường chéo vuông góc với nhau.

- Các cặp góc đối bằng nhau.

6. Hình bình hành

 

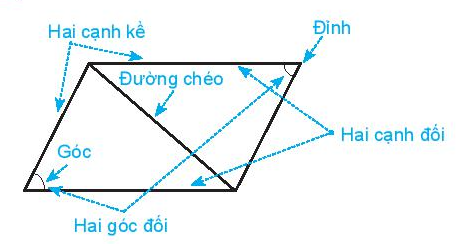
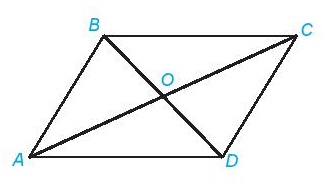
Trong hình bình hành:

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

- Các cặp cạnh đối song song.

- Các cặp góc đối bằng nhau.

7. Hình thang cân

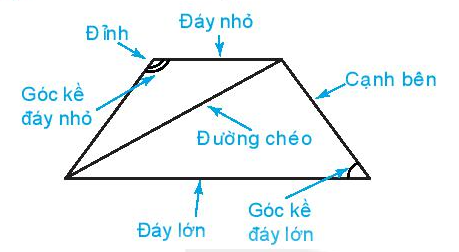
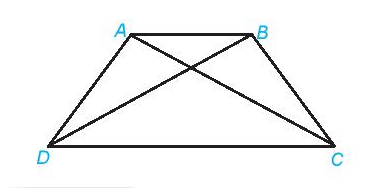
Trong hình thang cân:

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau.

- Hai cạnh đáy song song với nhau.

- Hai góc kề một đáy bằng nhau.

8. Công thức tính chu vi, diện tích hình vuông, hình chữ nhật và hình thang

Hình vuông cạnh a:

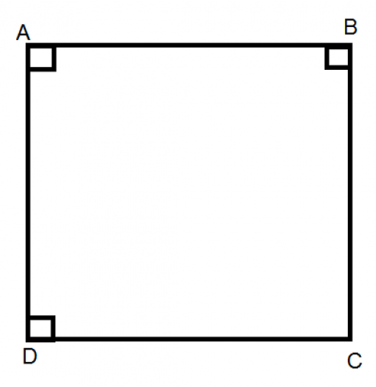
Chu vi: C = 4a.

Diện tích: S = a².

Hình chữ nhật có chiều dài là a, chiều rộng là b:

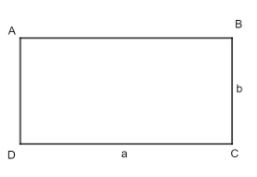
Chu vi: C = 2(a + b).

Diện tích: S = a.b.

Hình thang có độ dài hai cạnh đáy là a, b chiều cao h:

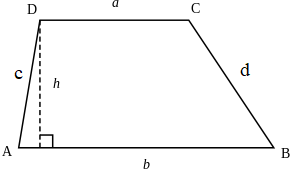
Chu vi: C = a + b + c + d.

Diện tích: S = (a + b).h:2.

9. Chu vi, diện tích hình bình hành, hình thoi.

Hình bình hành:

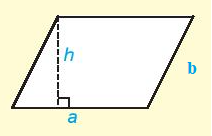
Chu vi: C = 2(a + b).

Diện tích: S = a.h.

Hình thoi:

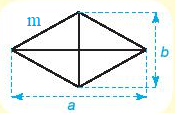
Chu vi: C = 4.m.

Diện tích: $S=\frac{1}{2}ab$.

B. Bài tập

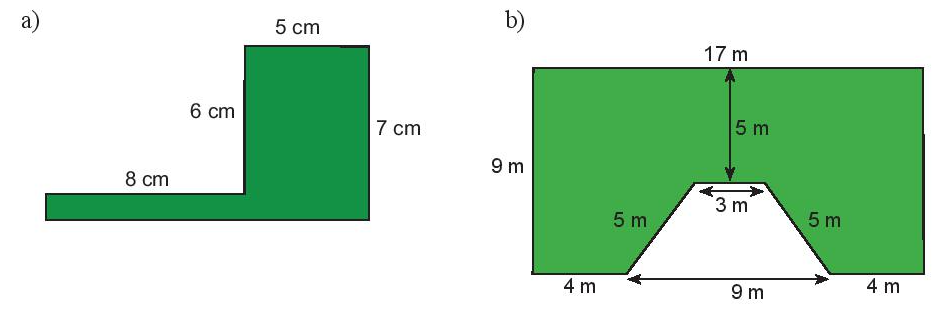
Bài 1. Tính diện tích và chu vi các hình được tô màu sau:

Lời giải

a)

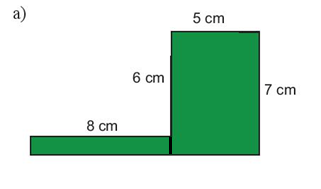
Chu vi của hình đã cho là: 8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).

Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:

Diện tích hình chữ nhật to là: $5.7=35\left(c{m}^2\right)$

Diện tích hình chữ nhật nhỏ là: $8.\left(7-6\right)=8\left(c{m}^2\right)$

Diện tích hình ban đầu là: $35+8=43\left(c{m}^2\right)$

Vậy diện tích hình được tô màu là   và chu vi hình được tô màu là 40 cm.

b)

 

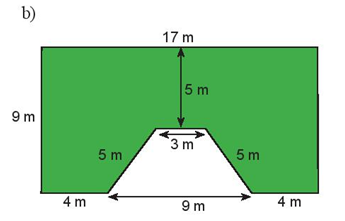
Chu vi hình được tô màu là: 9 + 4 + 5 + 3 + 5 + 4 + 9 + 17 = 56 (m).

Diện tích hình chữ nhật là: $9.17=153\left(m^2\right)$.

Diện tích hình thang cân là: $\left(9+3\right).\left(9-5\right):2=24\left(m^2\right)$.

Diện tích phần được tô màu bằng diện tích hình chữ nhật trừ đi diện tích hình thang cân màu trắng. Khi đó diện tích phần tô màu là: $\left(9+3\right).\left(9-5\right):2=24\left(m^2\right)$.

Vậy chu vi hình được tô màu là 56m, diện tích phần tô màu là $129m^2$.

Bài 2. Một mảnh vườn có hình dạng như hình vẽ bên. Để tính diện tích mảnh vườn, người ta chia nó thành hình thang cân ABCD và hình bình hành ADEF có kích thước như sau: BC = 30 m; AD = 42 m, BM = 22 m, EN = 28 m. Hãy tính diện tích mảnh vườn này.

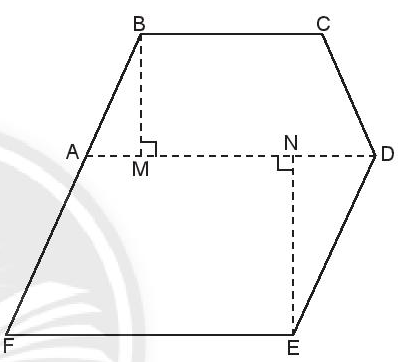
Lời giải

Diện tích hình thang cân ABCD là: $\left(30+42\right).22:2=792\left(m^2\right)$ .

Diện tích hình bình hành ADEF là: $42.28=1176\left(m^2\right).$

Diện tích mảnh vườn là: $792+1176=1968\left(m^2\right)$.

Vậy diện tích mảnh vườn là $1968m^2.$

Bài 3. Một khu vườn hình chữ nhật có chiều dài 25 m, chiều rộng 15 m. Ở giữa khu vườn người ta xây một bồn hoa hình thoi có độ dài hai đường chéo là 5 m và 3 m. Tính diện tích phần còn lại của khu vườn.

Lời giải

Diện tích khu vườn hình chữ nhật là: $25.15=375\left(m^2\right).$

Diện tích bồn hoa hình thoi là: $5.3:2=7,5\left(m^2\right).$

Diện tích phần còn lại của mảnh vườn là: $375–7,5=367,5\left(m^2\right).$

Vậy diện tích phần còn lại là $367,5m^2$.

I. Nhận biết

Câu 1. Hãy đếm xem trong hình bên có bao nhiêu hình vuông, bao nhiêu hình chữ nhật?

A. Có 4 hình vuông và 2 hình chữ nhật

B. Có 4 hình vuông và 4 hình chữ nhật

C. Có 5 hình vuông và 2 hình chữ nhật

D. Có 5 hình vuông và 4 hình chữ nhật

Hiển thị đáp án  

Đáp án: D

Giải thích:

Có 5 hình vuông bao gồm 4 hình vuông nhỏ và 1 hình vuông to.

Có 4 hình chữ nhật:

 

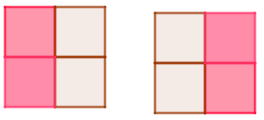
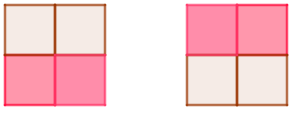
Câu 2. Hình đưới đây gồm các hình nào?

A. Hình tam giác đều, hình thoi, hình thang cân

B. Hình tam giác đều, hình bình hành, hình thang cân

C. Hình tam giác đều, hình bình hành, hình thang cân, hình lục giác đều

D. Hình tam giác đều, hình thoi, hình thang cân, hình lục giác đều

Hiển thị đáp án  

Đáp án: D

Giải thích:

Hình đã cho gồm các hình: Hình tam giác đều, hình thoi, hình thang cân và hình lục giác đều được xác định như sau:

- Hình tam giác đều

- Hình thoi

 

- Hình thang cân

- Hình lục giác đều

 

Câu 3. Cho hình vẽ sau:

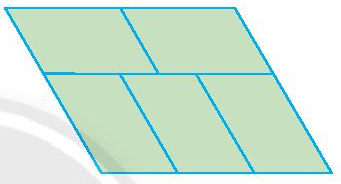
Phát biểu nào dưới đây là đúng?

A. Hình vẽ trên có 5 hình bình hành

B. Hình vẽ trên có 6 hình bình hành

C. Hình vẽ trên có 9 hình bình hành

D. Hình vẽ trên có 10 hình bình hành.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Hình vẽ trên có tất cả 10 hình bình hành.

Câu 4. Hình lục giác đều có tất cả các góc bằng nhau và bằng:

A. 60⁰

B. 90⁰

C. 120⁰

D. 180⁰

Hiển thị đáp án  

Đáp án: C

Giải thích:

Hình lục giác đều là hình có tất cả các góc bằng nhau và bằng 120⁰.

Câu 5. Cho hình vẽ:

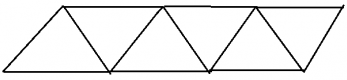
Hình vẽ trên được tạo thành từ bao nhiêu tam giác đều?

A. 5

B. 6

C. 7

D. 8

Hiển thị đáp án  

Đáp án: B

Giải thích:

Hình vẽ trên được ghép từ 6 hình tam giác đều.

Câu 6. Hãy đếm xem hình dưới đây có bao nhiêu hình thang cân, bao nhiêu hình lục giác đều.

A. 6 hình thang cân và 1 lục giác đều.

B. 5 hình thang cân và 1 lục giác đều.

C. 6 hình thang cân và 2 lục giác đều.

D. 5 hình thang cân và 2 lục giác đều.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Hình vẽ trên có tất cả 6 hình thang cân và 2 hình lục giác đều.

Câu 7.Trong giờ thảo luận nhóm, ba bạn Hùng, bạn Kiên, Minh phát biểu như sau:

- Bạn Hùng nói: “Hình thoi chỉ có tâm đối xứng và không có trục đối xứng”.

- Bạn Kiên nói: “Hình chữ nhật không có tâm đối xứng và chỉ có trục đối xứng”.

- Bạn Minh phát biểu: “Hình vuông có cả tâm đối xứng và trục đối xứng”.

Theo em, bạn nào phát biểu đúng?

A. Bạn Minh

B. Bạn Kiên

C. Bạn Hùng

D. Cả ba bạn đều đúng.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Hình thoi là hình có tâm đối xứng là giao điểm của hai đường chéo và hai trục đối xứng là hai đường chéo. Do đó phát biểu của bạn Hùng là SAI.

Hình chữ nhật có tâm đối xứng là giao điểm của hai đường chéo và có hai trục đối xứng nối trung điểm của hai cạnh đối diện. Do đó phát biểu của bạn Kiên SAI.

Hình vuông có tâm đối xứng là giao điểm của hai đường chéo và có bốn trục đối xứng bao gồm hai đường chéo và hai đường nối trung điểm của hai cạnh đối diện. Do đó phát biểu của bạn Minh ĐÚNG.

Vậy phát biểu của bạn Minh là đúng.

II. Thông hiểu

Câu 1. Hình thoi có độ dài hai đường chéo lần lượt là 50 m và 60 m thì diện tích là:

A. 300 $m^2$.                                     

B. 3 000 $m^2$.

C. 1 500 $m^2$.                                   

D. 150 $m^2$.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Diện tích hình thoi đã cho là:$50.60:2=1500m^2$

Câu 2. Cho hình bình hành ABCD có diện tích bằng 28 cm² và CD = 7cm. Vẽ AH vuông góc với CD và CK vuông góc với AB (Hình 42). Tính diện tích hình chữ nhật AHCK, biết BK = 2cm.

A. 20 cm²

B. 10 cm²

C. 14 cm²

D. 35 cm²

Hiển thị đáp án  

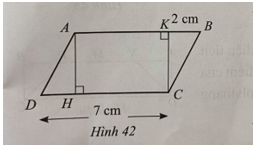
Đáp án: A

Giải thích:

Độ dài đường cao AH là: 28:7 = 4 (cm).

Độ dài cạnh AK bằng độ dài cạnh AB trừ đi độ dài cạnh BK và bằng: 7 – 2 = 5 (cm).

Diện tích hình chữ nhật AHCK là: 4.5 = 20 (cm²).

Vậy diện tích hình chữ nhật AHCK là 20 cm².

Câu 3. Hình thang cân có độ dài cạnh đáy và chiều cao lần lượt là 40 m, 30 m, 25 m, có diện tích là:

A. 1 750 $m^2$

B. 175 $m^2$

C. 875 $m^2$

D. 8 750 $m^2$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Diện tích hình thang cân là: $\left(40+30\right).25:2=875m^2$

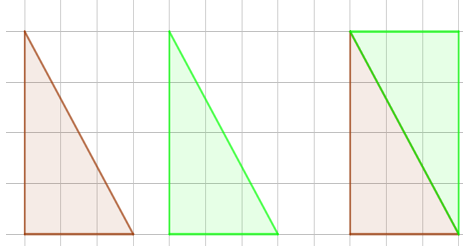
Câu 4. Từ hai tam giác vuông giống nhau ghép chúng lại có thể tạo thành:

A. Một hình chữ nhật.

B. Một hình bình hành.

C. Cả A và B đều sai

D. Cả A và B đều đúng

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ghép hai tam giác vuông thành hình chữ nhật như sau:

Ghép hai tam giác vuông thành hình bình hành như sau:

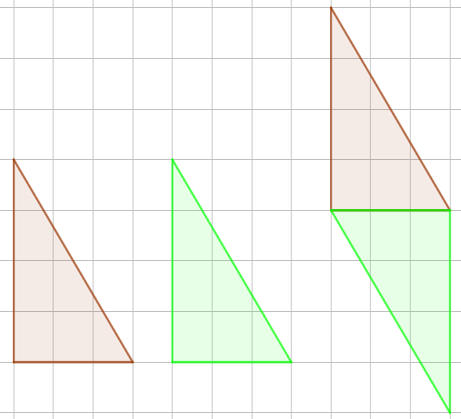
Vậy từ hai tam giác vuông bằng nhau ta có thể tạo được hình chữ nhật và hình bình hành.

Câu 5. Hình bình hành có chiều dài một cạnh và chiều cao tương ứng lần lượt là 70 dm và 50 dm có diện tích là:

A. 35 $m^2$

B. 3 500 $m^2$

C. 17,5 $m^2$

D. 350 $m^2$

Hiển thị đáp án  

Đáp án: A

Giải thích:

Diện tích hình bình hành là:$70.50=3500\left(d{m}^2\right)$

Đổi$3500d{m}^2=35m^2$

Câu 6. Một hình chữ nhật gồm 7 hình vuông. Trong đó A là hình vuông lớn nhất và B là hình vuông nhỏ nhất (Hình 44). Hình vuông A có diện tích gấp bao nhiêu lần diện tích hình vuông B.

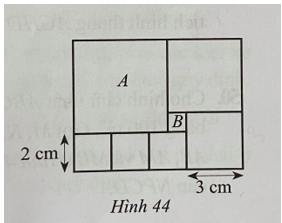
A. 5 lần

B. 2 lần

C. 25 lần

D. 4 lần

Hiển thị đáp án  

Đáp án: C

Giải thích:

Độ dài cạnh của hình vuông B là: 3 – 2 = 1 (cm).

Diện tích hình vuông B là: 1.1 = 1 (cm²).

Độ dài cạnh của hình vuông A là: 2.3 – 1 = 5 (cm).

Diện tích hình vuông A là: 5.5 = 25 (cm²).

Do đó diện tích hình vuông A gấp số lần diện tích hình vuông B là: 25:1 = 25 (lần).

Vậy diện tích hình vuông A gấp 25 lần diện tích hình vuông B. 

III. Vận dụng

Câu 1. Bác An muốn lát gạch một cái sân dạng hình chữ nhật có chiều dài và chiều rộng lần lượt là 12m và 9m. Tiền gạch là 130 000 đồng/m² và tiền công lát (tính cả vật liệu khác) là 70 000 đồng/m². Bác An phải trả tất cả bao nhiêu tiền?

A. 14 040 000 đồng

B. 7 560 000 đồng

C. 21 600 000 đồng

D. 19 600 000 đồng

Hiển thị đáp án  

Đáp án: C

Giải thích:

Cách 1:

Diện tích của sân hình chữ nhật là: 12.9 = 108 (m²).

Tiền gạch bác An phải trả là: 108. 130 000 = 14 040 000 (đồng).

Tiền công thợ bác An phải trả là: 108.70 000 = 7 560 000 (đồng).

Tổng số tiền bác An phải trả là: 14 040 000 + 7 560 000 = 21 600 000 (đồng).

Vậy số tiền bác An phải trả là: 21 600 000 đồng.

Cách 2:

Diện tích của sân hình chữ nhật là: 12.9 = 108 (m²).

Tổng số tiền bác An phải trả là:

108. 130 000 + 108.70 000

= 108.(130 000 + 70 000)

=108. 200 000 = 21 600 000 (đồng).

Vậy số tiền bác An phải trả là: 21 600 000 đồng.

Câu 2. Tính diện tích Hình 43 gồm một hình bình hành ABCD và một hình chữ nhật BCNM, biết BCNM có chu vi bằng 18cm và chiều dài gấp hai lần chiều rộng.

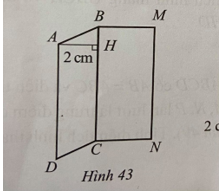
A. 9 cm²

B. 30 cm²

C. 18 cm²

D. 12 cm²

Hiển thị đáp án  

Đáp án: B

Giải thích:

Chiều rộng của hình chữ nhật BCNM là: (18:2):3 = 3 (cm).

Chiều dài của hình chữ nhật BCNM là: 2.3 = 6 (cm).

Diện tích hình chữ nhật BCNM là: 3.6 = 18 (cm²).

Diện tích hình bình hành ABCD với cạnh BC = 6cm và chiều cao tương ứng AH = 2cm là: 6.2 = 12 (cm²).

Diện tích Hình 43 bằng tổng diện tích hình bình hành ABCD là 12 cm² và diện tích hình chữ nhật BCNM là 18 cm² bằng: 12 + 18 = 30 (cm²).

Vậy diện tích hình 43 là 30 cm².

Câu 3. Cho các hình vuông ABCD, AHIJ, AEGF và H là trung điểm của đoạn BE (Hình 45). Độ dài các cạnh của các hình vuông nói trên theo đơn vị xăng – ti – met đều là các số tự nhiên. Tính diện tích hình vuông ABCD, biết rằng diện tích phần tô đậm là 19 cm².

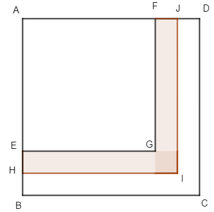
A. 19 cm²

B. 38 cm²

C. 121 cm²

D. 44 cm

Hiển thị đáp án  

Đáp án: C

Giải thích:

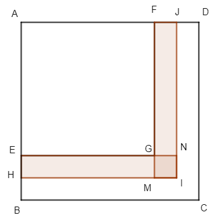
Đặt EG = a (cm), EH = b (cm).

Khi đó diện tích hình chữ nhật EGMH bằng hình chữ nhật GFJN bằng: a.b (cm²).

Diện tích hình vuông GNIM là: b.b = b² (cm²).

Diện tích phần tô đậm bằng tổng diện tích hình chữ nhật EGMH, diện tích hình chữ nhật GFJN và diện tích hình vuông GNIM bằng: ab + ab + b² = 2ab + b² = 19 (cm²).

Vì 2ab là số tự nhiên chẵn nên b² là số tự nhiên lẻ.

Hơn nữa b² < 19 nên b² = 1 hoặc b² = 9 suy ra b = 1 hoặc b = 3.

Với b = 1 thì a = 9 cm, khi đó AB = 9 + 1.2 = 11 cm.

Diện tích hình vuông ABCD là: 11.11 = 121 cm².

Với b = 3 thì 6a = 10, khi đó không có số tự nhiên a nào thỏa mãn nên loại.

Vậy diện tích hình vuông ABCD là 121 cm².

Câu 4. Cho hình thoi ABCD và hình bình hành EGCH (Hình 46). 

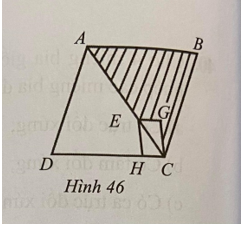
Phát biểu nào dưới đây là đúng?

A. Diện tích tứ giác AEHD bé hơn hai lần diện tích phần gạch chéo.

B. Diện tích tứ giác AEHD lớn hơn hai lần diện tích phần gạch chéo.

C. Diện tích tứ giác AEHD bé hơn diện tích phần gạch chéo 3 đơn vị diện tích.

D. Diện tích tứ giác AEHD bằng diện tích phần gạch chéo.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Trong hình thoi ABCD, ta có: diện tích tam giác ABC bằng diện tích tam giác ADC.

Trong hình bình hành AEHD, ta có: diện tích tam giác EGC bằng diện tích tam giác EHC.

Diện tích phần gạch chéo bằng diện tích tam giác ABC trừ diện tích tam giác EGC.

Diện tích tứ giác AEHD bằng diện tích tam giác ADC trừ diện tích tam giác EHC.

Do đó diện tích phần gạch chéo bằng diện tích tứ giác AEHD.

Câu 5. Hai đường chéo của hình thoi có độ dài là 160cm và 120 cm (Hình 47). Tính chiều cao của hình thoi, biết tỉ số giữa chiều cao và độ dài cạnh hình thoi là 24:25.

A. 16 cm

B. 36 cm

C. 72 cm

D. 96 cm

Hiển thị đáp án  

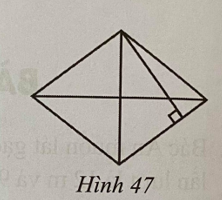
Đáp án: D

Giải thích:

Diện tích hình thoi là: 160.120:2 = 9 600 (cm²).

Vì tỉ số giữa chiều cao và độ dài cạnh hình thoi là 24:25 nên có thể coi chiều cao hình thoi là 24a và cạnh hình thoi là 25a.

Khi đó ta có diện tích hình thoi là: 25a.24a = 9 600 $\Rightarrow$a² = 16 $\Rightarrow$a = 4 cm.

Chiều cao của hình thoi là: 24.4 = 96 (cm).

Vậy chiều cao của hình thoi là 96cm. 

Câu 6. Cho hình chữ nhật ABCD. Gọi E, H, G lần lượt là trung điểm của AB, CD, EB (Hình 48). Tính tỉ số diện tích của diện tích hình thang GBCH và diện tích hình thang AGHD.

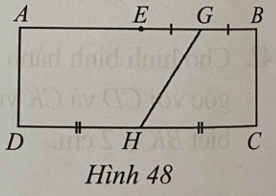
A. 3:4

B. 3:5

C. 1:4

D. 2:5

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có hình thang GBCH và hình thang AGHD có cùng chiều cao. Do đó tỉ số diện tích của diện tích hình thang GBCH và diện tích hình thang AGHD bằng tỉ số tổng độ dài hai đáy của hình thang GBCH và tổng độ dài hai đáy của hình thang AGHD.

Đặt GB = GE = a suy ra CH = 2a, AB = 4a, AG = 3a.

Tổng độ dài hai đáy hình thang GBCH là: 2a + a = 3a.

Tổng độ dài hai đáy hình thang AGHD là: 2a + 3a = 5a.

Suy ra tỉ số tổng độ dài hai đáy của hình thang GBCH và tổng độ dài hai đáy của hình thang AGHD là 3:5.

Vậy tỉ số diện tích của diện tích hình thang GBCH và diện tích hình thang AGHD là 3:5. 

Câu 7. Cho hình chữ nhật ABCD có AB = 4BC và diện tích bằng 100 m². Gọi M, N, P lần lượt trung điểm của AB, AM và MB (Hình 49). Tính diện tích của hình thang cân NPCD.

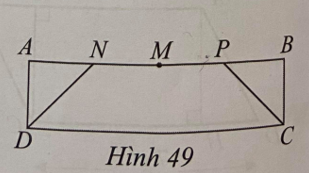
A. 100 m²

B. 150 m²

C. 75 m²

D. 25 m²

Hiển thị đáp án  

Đáp án: C

Giải thích:

Đặt BC = a (m) suy ra AB = 4a (m)

Diện tích hình chữ nhật ABCD là: a.4a = 4a² (m²).

Mà diện tích hình chữ nhật ABCD bằng 100m² nên 4a² =100 $\Rightarrow$a² = 25 $\Rightarrow$a = 5 m.

Suy ra BC = 5 m, AB = 20 m.

Khi đó NP = AB:2 = 20:2 = 10 m.

Ta có hình thang cân NPCD có chiều cao là BC = 5 m.

Diện tích hình thang cân NPCD là: (20 + 10).5:2 = 75 m².

Vậy diện tích hình thang cân NPCD là 75 m². 

Câu 8. Để làm một con diều, bạn Nam lấy một tờ giấy hình chữ nhật có chiều dài 60 cm, chiều rộng 40 cm để cắt thành một hình thoi như hình bên dưới. Hãy tính diện tích của con diều.

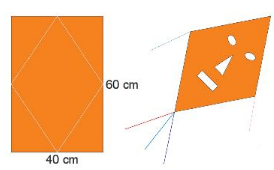
A. 12 cm²

B. 120 cm²

C. 1 200 cm²

D. 12 000 cm²

Hiển thị đáp án  

Đáp án: C

Giải thích:

Chiều dài và chiều rộng của hình chữ nhật chính là độ dài của hai đường chéo của hình thoi nên diện tích của con diều hình thoi là:

$60.40:2=1200\left(c{m}^2\right)$

Vậy diện tích con diều là $1200c{m}^2$