TOP 32 câu hỏi Trắc nghiệm ôn tập chương 3 có lời giải - Toán lớp 6 Kết nối tri thức

Trắc nghiệm Toán 6 Bài: ôn tập chương 3

A. Lý thuyết

I. Tập hợp các số nguyên

1. Làm quen với số nguyên âm

- Các số tự nhiên (khác 0) 1; 2; 3; 4; … còn được gọi là các số nguyên dương.

- Các số - 1; -2; -3; … gọi là các số nguyên âm.

- Tập hợp $\mathbb{Z}$ gồm các số nguyên âm, số 0 và số nguyên dương gọi là tập hợp số nguyên.

$\mathbb{Z}=\left\{\mathrm{...};-3;-2;-1;0;1;2;3;\mathrm{...}\right\}$.

Chú ý:

Số 0 không là số nguyên âm, cũng không phải là số nguyên dương.

Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn số 6 còn được viết là +6 (đọc là “dương sáu”).

2. Thứ tự trong tập số nguyên

Trục số:

Ta biểu diễn các số 0; 1; 2; 3; 4; 5 … và các số nguyên âm -1; -2; -3; 4; 5… như sau:

+ Chiều từ trái sang phải là chiều dương, chiều ngược lại là chiều âm.

+ Điểm biểu diễn số nguyên a được gọi là điểm a.

+ Cho hai số nguyên a và b. Trên trục số, nếu điểm a nằm trước điểm b thì số a nhỏ hơn số b, kí hiệu a < b.

So sánh hai nguyên:

Mọi số nguyên âm đều nhỏ hơn 0, do đó nhỏ hơn mọi số nguyên dương.

Nếu a, b là hai số nguyên dương và a > b thì – a < - b.

II. Phép cộng và phép trừ số nguyên

1. Cộng hai số nguyên cùng dấu

Quy tắc cộng hai số nguyên âm

Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “-“ trước kết quả.

2. Cộng hai số nguyên khác dấu

Hai số đối nhau:

Hai số nguyên a và b được gọi là đối nhau nếu a và b nằm khác phía với điểm 0 và có cùng khoảng cách đến gốc 0.

Chú ý:

Ta quy ước số đối của 0 là chính nó.

Tổng của hai số đối nhau luôn bằng 0.

Quy tắc cộng hai số nguyên khác dấu:

+ Hai số nguyên đối nhau thì có tổng bằng 0.

+ Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phân số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.

3. Tính chất của phép cộng

Phép cộng số nguyên có tính chất sau:

+ Giao hoán: a + b = b + a;

+ Kết hợp: (a + b) + c = a + (b + c).

4. Trừ hai số nguyên

Quy tắc trừ hai số nguyên

Muốn trừ số nguyên a cho số nguyên b, ta cộng số nguyên a với số đối của số nguyên b:

a – b = a + (-b).

III. Quy tắc dấu ngoặc

Bỏ dấu ngoặc trong trường hợp đơn giản

Các số âm (hay dương) trong một dãy tính thường được viết trong dấu ngoặc. Nhờ quy tắc cộng hay trừ số nguyên, ta có thể viết dãy tính dưới dạng không có dấu ngoặc.

Vì phép trừ chuyển được về phép cộng nên các dãy tính như trên cũng được gọi là một tổng.

Quy tắc dấu ngoặc:

Khi bỏ dấu ngoặc có dấu “+” đằng trước, ta giữ nguyên dấu của các số hạng trong ngoặc;

Khi bỏ dấu ngoặc có dấu “-” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “+” đổi thành “-” và dấu “-” đổi thành dấu “+”.

IV. Phép nhân số nguyên

1. Nhân hai số nguyên khác dấu

Quy tắc nhân hai số nguyên khác dấu

Muốn nhân hai số nguyên khác dấu, ta nhân phần số tự nhiên của hai số đó với nhau rồi đặt dấu “-” trước kết quả nhận được.

Nếu $m,n\in {\mathbb{N}}^{*}$ thì m.(-n) = (-n).m = - (m.n).

2. Nhân hai số nguyên cùng dấu

Quy tắc nhân hai số nguyên âm

Muốn nhân hai số nguyên âm, ta nhân phần số tự nhiên của hai số đó với nhau.

Nếu $m,n\in {\mathbb{N}}^{*}$  thì (-m).(-n) = (-n).(-m) = m.n.

3. Tính chất của phép nhân

Phép nhân các số nguyên có các tính chất:

Giao hoán: a.b = b.a;

Kết hợp: (a.b).c = a.(b.c);

Phân phối của phép nhân đối với phép cộng: a.(b + c) = a.b + a.c.

V. Phép chia hết. Ước và bội của một số nguyên

1. Phép chia hết

Cho $a,b\in \mathbb{Z}$ với $b\ne 0$. Nếu có số nguyên q sao cho  a = b.q thì ta có phép chia hết a:b = q (trong đó ta cũng gọi a là số bị chia, b là số chia và q là thương). Khi đó ta nói a chia hết cho b, kí hiệu a $⋮$ b.

2. Ước và bội

Khi a $⋮$ b $\left(a,b\in \mathbb{Z},b\ne 0\right)$, ta còn gọi a là một bội của b và b là một ước của a.

Nhận xét:

Nếu a là một bội của b thì –a cũng là một bội của b.

Nếu b là một ước của a thì – b cũng là một ước của a.

B. Bài tập

Bài 1. Dùng số âm để diễn tả các thông tin sau:

a) Ở nơi lạnh nhất thế giới, nhiệt độ có thể xuống đến 60⁰C dưới 0⁰C.

b) Do dịch bệnh, một công ty trong một tháng đã bị lỗ 2 triệu đồng.

Lời giải

a) Ở nơi lạnh nhất thế giới, nhiệt độ có thể xuống đến - 60⁰C.

b) Do dịch bệnh, một công ty một tháng có – 2 triệu đồng.

Bài 2. Tính một cách hợp lí:

a) 15.(-236) + 15.235;

b) 237.(-28) + 28.137;

c) 38.(27 – 44) – 27.(38 – 44).

Lời giải

a) 15.(-236) + 15.235

= 15.[(-236) + 235]

= 15.(-1)

= -15.

b) 237.(-28) + 28.137

= (-237).28 + 28.137

= 28.[(-237) + 137]

= 28.(-100)

= -2 800.

c) 38.(27 – 44) – 27.(38 – 44).

= 38.27 – 38.44 – 27.38 + 27.44

= 38.27 – 27.38 – 38.44 + 27.44

= 0 + 44.(-38 + 27)

= 0 + 44.(-11)

= - 484.

Bài 3. Có hay không hai số nguyên a và b mà hiệu a – b :

a) Lớn hơn cả a và b?

b) Lớn hơn a nhưng nhỏ hơn b?

Lời giải

a) Có trường hợp a – b > a hoặc a – b > b

Ví dụ: a = 10 và b = - 15

Ta có a – b = 10 – (-15) = 10 + 15 = 25.

Khi đó 25 > 15 và 25 > - 15.

b) Có trường hợp hiệu a – b lớn hơn a nhưng nhỏ hơn b:

Ví dụ: a = - 3, b = -1, a – b = -3 – (-1) = -2 .

Vì -3 < -2 < -1 hay a < a – b < b.

I. Nhận biết

Câu 1. Chọn phát biểu đúng trong số các câu sau:

(A) Tập hợp số nguyên được kí hiệu là N.

(B) +2 không phải là một số tự nhiên.

(C) 4 không phải là một số nguyên.

(D) – 5 là một số nguyên.

Hiển thị đáp án  

Đáp án: D

Giải thích:

(A) Tập hợp số nguyên được kí hiệu là Z. Nên A sai.

(B) + 2 là một số tự nhiên nên B sai.

(C) 4 là một số nguyên nên C sai.

(D) – 5 là một số nguyên âm nên – 5 là một số nguyên nên D đúng.

Câu 2. Trong các phát biểu sau đây, phát biểu nào sai?

(A) 3 > - 4.                                     

(B) – 5 > - 9.

(C) – 1 < 0.                                     

(D) – 9 > -8.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Vì trên trục số điểm – 9 nằm bên trái -8 nên  -9 < -8. Do đó D sai.

Câu 3. Tính các thương sau: (- 14):(- 7).

A. – 2

B. 2

C. 4

D. -4

Hiển thị đáp án  

Đáp án: B

Giải thích:

(- 14):(- 7) = 14 : 7 = 2.

II. Thông hiểu

Câu 1. Kết quả của phép tính: 25 – (9 – 10) + (28 – 4) là:

A. 50.

B. 2.

C. – 2

D. 48.

Hiển thị đáp án  

Đáp án: A

Giải thích:

25 – (9 – 10) + (28 – 4)

= 25 – (- 1) + 24

= 25 + 1 + 24

= 26 + 24

= 50.

Câu 2. Kết quả của phép tính: (- 4) . (+21) . (- 25) . (- 2) là:

A. 420

B. 4 200

C. – 4 200

D. - 420.

Hiển thị đáp án  

Đáp án: C

Giải thích:

(- 4) . (+21) . (- 25) . (- 2)

= [(-4) . (-25)] . [(+21) . (-2)] (tính chất giao hoán và kết hợp)

= 100 . (-42)

= - 4 200.

Câu 3. Tính: (- 45) – (27 – 8).

A. 64

B. -26

C. -64

D. 26

Hiển thị đáp án  

Đáp án: C

Giải thích:

(- 45) – (27 – 8) = (-45) – 19 = (-45) + (-19) = -64.

Câu 4. Tìm số nguyên x, thỏa mãn: $x^2=81.$

A. x = 9

B. x = -9

C. x = 9 hoặc x = -9

D. x = 3

Hiển thị đáp án  

Đáp án: C

Giải thích:

x^222222223232 = 81

x² = 9² hoặc x² = (-9)²

x = 9 hoặc x = - 9.

Vậy x = 9 hoặc x = - 9.

Câu 5. Cho biết năm sinh của một số nhà toán học.

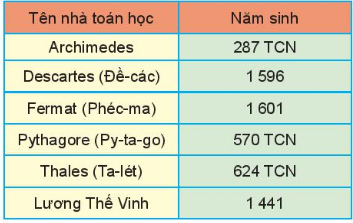
Em hãy sắp xếp các nhà toán học theo thứ tự giảm dần của năm sinh.

A. Fermat; Descartes; Lương thế Vinh; Archimedes; Pythagore; Thales

B. Fermat; Descartes; Lương thế Vinh; Pythagore; Thales; Archimedes

C. Fermat; Descartes; Lương thế Vinh; Thales; Pythagore; Archimedes

D. Fermat; Lương thế Vinh; Descartes; Thales; Pythagore; Archimedes

Hiển thị đáp án  

Đáp án: A

Giải thích:

Archimedes có năm sinh 287 TCN nghĩa là năm thứ -287;

Pythagore có năm sinh 570 TCN nghĩa là năm thứ - 570;

Thales có năm sinh 624 TCN nghĩa là năm thứ - 624;

Ta có: 1 601 > 1 596 > 1 441 > - 287 > - 570 > - 624.

Các nhà bác học theo thứ tự năm sinh giảm dần: Fermat; Descartes; Lương thế Vinh; Archimedes; Pythagore; Thales.

Câu 6. Nhận xét nào sau đây đúng về kết quả của phép tính: (2 021 – 39) + [(-21) + (-61)];

A. Kết quả là một số nguyên âm

B. Kết quả là một số nguyên dương lớn hơn 2 000

C. Kết quả là một số nguyên dương nhỏ hơn 2 000

D. Kết quả bằng 0 

Hiển thị đáp án  

Đáp án: A

Giải thích:

(2 021 – 39) + [(-21) + (-61)]

= 2 021 + (-39) + (-21) + (-61)

= [2 021 + (-21)] + [(-39) + (-61)]

= 2 000 + (-100)

= 2 000 – 100

= 1 900 < 2 000

Câu 7. Một máy bay đang bay ở độ cao 5 000 m trên mực nước biển, tình cờ thẳng ngay bên dưới máy bay có một chiếc tàu ngầm đang lặn ở độ sâu 1 200 m dưới mực nước biển. Tính khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm.

A. 4 800 m

B. – 720 m

C. 7 200 m

D. 6 200 m

Hiển thị đáp án  

Đáp án: D

Giải thích:

Độ cao của tàu ngầm là: -1200 m.

Khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm là:

5 000 – (-1 200) = 5 000 + 1 200 = 6 200 (m)

Vậy khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm là 6 200 m.

Chọn D

Câu 8. Hình vẽ dưới đây biểu diễn một người đi từ O đến A rồi quay về B. 

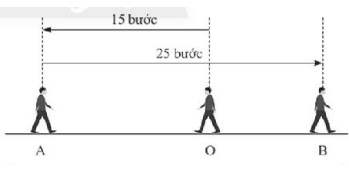
Hỏi nếu người đó đi thẳng từ O đến B thì hết bao nhiêu bước?

A. 30 bước

B. 20 bước

C. 15 bước

D. 10 bước

Hiển thị đáp án  

Đáp án: D

Giải thích:

Người đó đi từ O đến B hết số bước chân là: 25 -15 = 10 ( bước).

Câu 9. Tìm số nguyên x, biết: (-300):20 + 5.(3x – 1) = 25

A. x = 1

B. x = 3

C. x = -1

D. x = -3

Hiển thị đáp án  

Đáp án: B

Giải thích:

(-300):20 + 5.(3x – 1) = 25

(-15) + 5.(3x – 1) = 25

5.(3x – 1) = 25 – (-15)

5.(3x – 1) = 40

3x – 1 = 8

3x = 9

x = 3.

Vậy x = 3.

III. Vận dụng

Câu 1. Một công ty có 3 cửa hàng A, B, C. Kết quả kinh doanh sau một năm của từng cửa hàng như sau: 

Cửa hàng A: lãi 225 triệu đồng. 

Cửa hàng B: lỗ 280 triệu đồng. 

Cửa hàng C: lãi 655 triệu đồng. 

Hỏi bình quân mỗi tháng công ty lãi hay lỗ bao nhiêu tiền từ ba cửa hàng đó?

A. 386,7 triệu

B. 630 triệu

C. 600 triệu

D. 50 triệu

Hiển thị đáp án  

Đáp án: D

Giải thích:

Cửa hàng A lãi 225 triệu đồng được biểu diễn: 225 (triệu đồng).

Cửa hàng B lỗ 280 triệu đồng được biểu diễn: - 280 (triệu đồng).

Cửa hàng C lãi 655 triệu đồng được biểu diễn: 655 (triệu đồng).

Tổng kết quả kinh doanh trong 12 tháng của ba cửa hàng A, B, C là:

225 + (-280) + 655 = 600 (triệu đồng).

Mỗi tháng doanh thu của công ty là: 600:12 = 50 (triệu đồng).

Vậy bình quân mỗi tháng công ty lãi 50 triệu đồng từ ba cửa hàng A, B, C.

Câu 2. Tính một cách hợp lí: (-16).125.[(-3).2²].5³ – 2.10⁶

A. 10⁴

B. 10⁵

C. 10⁶

D. 10⁷

Hiển thị đáp án  

Đáp án: A

Giải thích:

-16).125.[(-3).2²].5³ – 2.10⁶

= (-16).125.(-3).4.125 – 2.10⁶

= (-2).8.125.(-3).4.125 – 2.10⁶

= (-2).4.125.8.125.(-3) – 2.10⁶

= (-1 000).1 000.(-3) – 2.10⁶

= 3.10⁶ – 2.10⁶

= 10⁶.(3 – 2)

= 10⁶.

Câu 3. Tìm số nguyên x, biết: (5.13)^x = 25.(5³ + 4.11)² : (3⁴ – 3⁵:3³ + 97) (x0)

A. Không có giá trị nguyên của x

B. x = 1

C. x = 5

D. x = 2

Hiển thị đáp án  

Đáp án: D

Giải thích:

b) (5.13)^x = 25.(5³ + 4.11)² : (3⁴ – 3⁵:3³ + 97) (x0)

65^x = 25.(125 + 44)² : (81 – 3² + 97)

65^x = 25.169² : (81 – 9 + 97)

65^x = 25.169² : 169

65^x = 25.169

65^x = 5².13²

65^x = (5.13)²

65^x = (65)²

x = 2 (thỏa mãn điều kiện)

Vậy x = 2.

Câu 4. Tính một cách hợp lí: (134 – 34).(-28) + 72.[(-55) – 45].

A. 10 000

B. 1 000

C. – 10 000

D. – 100 000

Hiển thị đáp án  

Đáp án: C

Giải thích:

(134 – 34).(-28) + 72.[(-55) – 45]

= 100.(-28) + 72.(-100)

= 100(-28) + (-72).100

= 100.[(-28) + (-72)]

= 100.(-100)

= - 10 000.

Câu 5. Có bao nhiêu giá trị nguyên của x, thỏa mãn: (x + 1).(x – 4) < 0.

A.Vô số

B. 3

C. 0

D. 4

Hiển thị đáp án  

Đáp án: D

Giải thích:

(x + 1).(x – 4) < 0.

Ta có x + 1 > x – 4

Mà x + 1 và x – 4 trái dấu

Nên x + 1 > 0 và x – 4 < 0

Suy ra x > - 1 và x < 4

Hay – 1 < x < 4.

Do x là số nguyên nên x {0; 1; 2; 3}.

Vậy x {0; 1; 2; 3}.

Câu 6. Tìm khoảng giá trị thích hợp của chữ số a, sao cho: $\overline{a40}:10<23;$

A. 0 < a < 1

B. a > 1

C. 0 < a < 2

D. a < 0

Hiển thị đáp án  

Đáp án: C

Giải thích:

Nhân cả hai vế với 10, ta được:

$\overline{a40}<23.10=230.$

Do đó a chỉ có thể bằng 1.

Vậy a = 1.

Suy ra 0 < a < 2.

Câu 7. Tính A – B, biết rằng A là tích của các số nguyên âm chẵn có một chữ số và B là tổng của các số nguyên dương lẻ có hai chữ số.

A. – 2 091

B. 384

C. 2 475

D. - 1 909

Hiển thị đáp án  

Đáp án: A

Giải thích:

Các số nguyên âm chẵn có một chữ số là: - 2; - 4; - 6; - 8.

Khi đó A = (-2).(-4).(-6).(-8)

= 384.

Các số nguyên lẻ có hai chữ số là: 11; 13; 15; …; 99.

B = 11 + 13 + 15 + … + 97 + 99

= (11 + 99) + (13 + 97) + …+ (53 + 57) + 55

= 110 + 110 + … + 110 + 55 (22 số 110)

= 110.22 + 55

= 2 420 + 55

= 2 475.

Suy ra A – B = 384 – 2 475 = - 2091.

Vậy A – B = - 2 091.

Câu 8. Tìm số tự nhiên n nhỏ nhất sao cho n vừa là tổng của 5 số tự nhiên liên tiếp, vừa là tổng của 7 số tự nhiên liên tiếp.

A. n = 5

B. n = 7

C. n = 70

D. n = 35

Hiển thị đáp án  

Đáp án: D

Giải thích:

Ta có n = a + (a + 1) + (a + 2) + (a + 3) + (a + 4) với a là số tự nhiên

Khi đó n = 5a + 10 = 5.(a + 2) chia hết cho 5.

Ta lại có n = b + (b + 1) + (b + 2) + (b + 3) + (b + 4) + (b + 5) + (b + 6) với b là số tự nhiên.

Khi đó n = 7b + 21 = 7.(b + 3) chia hết cho 7.

Do đó n vừa chia hết cho 5 vừa chia hết cho 7 nên n là bội chung của 5 và 7.

Mà n là nhỏ nhất nên n là BCNN(5; 7).

Ta có 5 = 5, 7 = 7.

BCNN(5, 7) = 5.7 = 35.

Vậy n = 35.

Câu 9. Tìm số nguyên x, biết: 2x – 1 là bội của x – 3

A. x = 2

B. x thuộc {-1; 2}

C. x thuộc {-1; 0; 2; 3}

D. x thuộc {0; 2; 3}

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có 2x – 1 là bội của x – 3 nên 2x – 1 chia hết cho x – 3.

Ta lại có 2x – 1 = 2x – 6 + 5 = 2(x – 1) + 5.

Vì 2(x – 1) chia hết cho x – 1 nên 5 phải chia hết cho x – 1 hay x – 1 thuộc Ư(5) = {1; -1; 2; -2}.

Suy ra x thuộc {2; 0; 3; -1}.

Vậy x {2; 0; 3; -1}.

Câu 10. Tìm số nguyên x, sao cho: A = x² + 2 021 đạt giá trị nhỏ nhất.

A. x = 2 021

B. Không tồn tại giá trị x nguyên thỏa mãn A đạt GTNN

C. Có vô số giá trị nguyên của x thỏa mãn A đạt GTNN

D. x = 0

Hiển thị đáp án  

Đáp án: D

Giải thích:

Vì $x^2\ge 0$ với moi giá trị nguyên của x nên $x^2+2021\ge 2021$.

Dấu “=” xảy ra khi x² = 0 hay x = 0.

Vậy A đạt giá trị nhỏ nhất 2 021 tại x = 0.