TOP 28 câu hỏi Trắc nghiệm Bài 10: Số nguyên tố (có đáp án 2022) - Toán lớp 6 Kết nối tri thức
Bộ 28 câu hỏi trắc nghiệm Toán lớp 6 Bài 10: Số nguyên tố có đáp án đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 6 Bài 10.
Trắc nghiệm Toán 6 Bài 10: Số nguyên tố
A. Lý thuyết
1. Số nguyên tố và hợp số
- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
- Hợp số là số tự nhiên lơn hơn 1, có nhiều hơn hai ước.
Ví dụ 1. Trong các số đã cho dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao?
190; 11; 132; 23; 43; 17; 21.
Lời giải
Ta thấy 190 có các ước là 1, 2, 5, 190 nhiều hơn hai ước nên 190 là hợp số;
11 chỉ có ước là 1 và 11 nên 11 là số nguyên tố;
132 có các ước là 1; 2; 132 nhiều hơn hai ước nên 132 là hợp số;
23 chỉ có ước là 1 và 23 nên 23 là số nguyên tố;
43 chỉ có ước là 1 và 43 nên 43 là số nguyên tố;
17 chỉ có ước là 1 và 17 nên 17 là số nguyên tố;
21 có các ước là 1; 3; 7; 21 nhiều hơn hai ước nên 21 là hợp số.
2. Phân tích một số ra thừa số nguyên tố
Mọi số đều có thể phân tích ra tích của các thừa số nguyên tố
Cách phân tích một số ra thừa số nguyên tố:
+) Phương pháp phân tích bằng sơ đồ cây
Ví dụ 2. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cây:
Lời giải
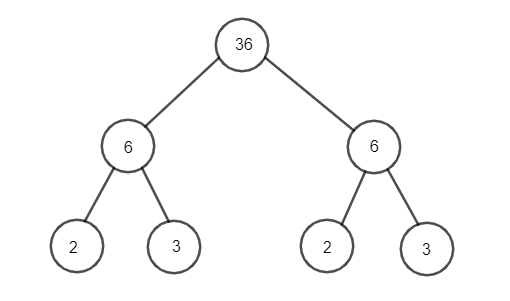
Vậy 36=22.32.
+) Phương pháp phân tích bằng sơ đồ cột
Ví dụ 3. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cột:
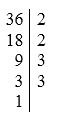
Vậy 36=22.32 .
B. Bài tập
Bài 1. Phân tích các số sau ra thừa số nguyên tố: 60; 121; 225.
Lời giải
Ta sẽ sử dụng sơ đồ cột
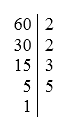
Vậy 60=22.3.5
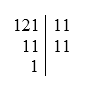
Vậy 121=112
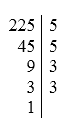
Vậy 225=32.52
Bài 2. Các khẳng định sau đúng hay sai? Vì sao?
a) Ước nguyên tố của 12 là 1; 2; 3.
b) Tích hai số nguyên tố bất kì luôn là số chẵn.
c) Mọi số chẵn đều là hợp số.
d) Mọi số lẻ đều là số nguyên tố.
Lời giải
a) 1; 2; 3 là các ước của 12, trong đó 2 và 3 là số nguyên tố còn 1 không phải là số nguyên tố nên a sai.
b) Ta có 3 và 5 là hai số nguyên tố. Tích 3.5 = 15 không phải là số chẵn. Do đó b sai.
c) Số 2 là số chẵn nhưng 2 là số nguyên tố nên c sai.
d) Ta có 15 là số lẻ nhưng 15 không phải là số nguyên tố. Do đó d sai.
I. Nhận biết
Câu 1. Số nào trong các số sau là số nguyên tố?
A. 3;
B. 8;
C. 12;
D. 15.
Đáp án: A
Giải thích:
Trong các số đã cho:
3 có hai ước là 1 và 3. Do đó 3 là số nguyên tố.
8 có 4 ước là 1; 2; 4; và 8 nên 8 là hợp số.
12 có 6 ước là 1; 2; 3; 4; 6 và 12 nên 12 là hợp số.
15 có 4 ước là 1; 3; 5 và 15 nên 15 là hợp số.
Câu 2. Trong các số sau: 16; 17; 20; 21; 23; 97. Có bao nhiêu số là hợp số?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: D
Giải thích:
16 có 5 ước là 1; 2; 4; 8; 16 nên 16 là hợp số.
17 có 2 ước là 1 và 17 nên 17 là số nguyên tố.
20 có 6 ước là 1; 2; 4; 5; 10 và 20 nên 20 là hợp số.
21 có 4 ước là 1; 3; 7 và 21 nên 21 là hợp số.
23 có 2 ước là 1 và 23 nên 23 là số nguyên tố.
97 có 2 ước là 1 và 97 nên 97 là số nguyên tố.
Vậy có 3 số là hợp số.
Câu 3. Hoàn thành phát biểu sau: “Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có …”:
A. ước là 1.
B. ước là chính nó.
C. duy nhất một ước.
D. hai ước là 1 và chính nó.
Đáp án: D
Giải thích:
Câu 4. Cho A là tập hợp các số nguyên tố nhỏ hơn 30. Chọn đáp án đúng.
A. 1∈A;
B. 2∉A;
C. 29∉A;
D. 17∈A.
Đáp án: D
Giải thích:
Các số nguyên tố nhỏ hơn 30 bao gồm: 2; 3; 5; 7; 11; 13; 17; 23; 29.
Do đó A = {2; 3; 5; 7; 11; 13; 17; 23; 29}.
Ta có 1 không thuộc tập A, ta viết 1∉A nên A sai.
Ta có 2 thuộc tập A, ta viết 2∈A nên B sai.
Ta có 29 thuộc tập A, ta viết 29∈A nên C sai.
Ta có 17 thuộc tập A, ta viết 17∈A nên D đúng.
Câu 5. Phân tích một số ra thừa số nguyên tố là:
A. phân tích số đó thành tích của số nguyên tố với các hợp số.
B. phân tích số đó thành tích của các số tự nhiên.
C. Phân tích số đó thành tích của các thừa số nguyên tố.
D. Phân tích số đó thành tích của hai thừa số nguyên tố.
Đáp án: D
Giải thích:
Phân tích một số ra thừa số nguyên tố là phân tích số đó thành tích của các thừa số nguyên tố.
Câu 6. Có bao nhiêu cách để phân tích một số ra thừa số nguyên tố?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: B
Giải thích:
Có hai cách phân tích một số ra thừa số nguyên tố là:
+ Phương pháp phân tích theo sơ đồ cây;
+ Phương pháp phân tích theo sơ đồ cột.
Câu 7. Có bao nhiêu khẳng định đúng trong các khẳng định sau?
a) Ước nguyên tố của 18 là 1; 2; và 3.
b) Tích của hai số nguyên tố bất kì luôn là số lẻ.
c) Mọi số chẵn đều là hợp số.
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: A
Giải thích:
Ước nguyên tố của 18 chỉ có 2 và 3, 1 không phải số nguyên tố nên a sai.
2 là số nguyên tố, 3 là số nguyên tố. Ta có tích 2.3 = 6 là số chẵn nên b sai.
Ta có 2 là số chẵn, 2 cũng là số nguyên tố nên c sai.
Vậy không có phát biểu nào đúng.
Câu 8. Tìm chữ số a để ¯49a là số nguyên tố:
A. 1;
B. 9;
C. A và B đều đúng;
D. cả A và B đều sai.
Đáp án: C
Giải thích:
Dựa vào bảng số nguyên tố ở cuối sách giáo khoa ta có:
491 và 499 là hai số nguyên tố nên a = 1 hoặc a = 9.
II. Thông hiểu
Câu 1. Phân tích 70 ra thừa số nguyên tố ta được: 70 = 2x.5y.7z. Tổng x + y + z = ?
A. 3;
B. 4;
C. 5;
D. 6.
Đáp án: A
Giải thích:
Ta có:
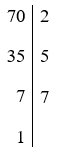
Vậy 70 = 2.5.7.
Suy ra x = 1; y = 1; z = 1.
Do đó x + y + z = 1 + 1 + 1 = 3.
Câu 2. Hoàn thành sơ đồ cây sau:
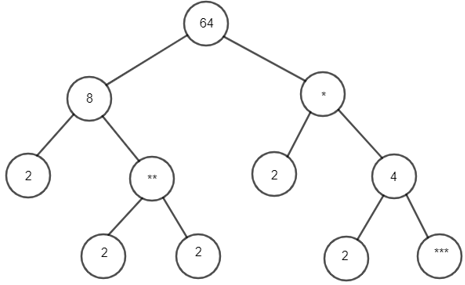
A. * = 8; ** = 2; *** = 4.
B. * = 4; ** = 8; *** = 2.
C. * = 8; ** = 4; *** = 2.
D. * = 4; ** = 2; *** = 8.
Đáp án: C
Giải thích:
Sơ đồ cây hoàn chỉnh là:
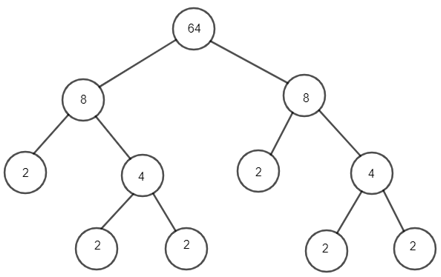
Vậy * = 8; ** = 4; *** = 2.
Câu 3. Phân tích số 75 ra thừa số nguyên tố là:
A. 75 = 3.25;
B. 75 = 15.5;
C. 75 = 3.52;
D. 75 = 75.1.
Đáp án: C
Giải thích:
Ta có:
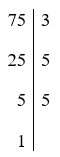
Suy ra 75 = 3.52.
Câu 4. Bạn Nam phân tích số 120 ra thừa số nguyên tố như sau: 120 = 23.3.5.
Bạn An phân tích 105 ra thừa số nguyên tố như sau: 105 = 3.5.7.
Chọn đáp án đúng.
A. Bạn Nam;
B. Bạn An;
C. Cả Nam và An đều sai.
D. Cả Nam và An đều đúng.
Đáp án: D
Giải thích:
Ta có:
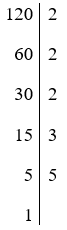
Vậy 120 = 23.3.5. Do đó Nam đúng.
Ta có
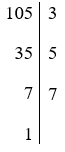
Vậy 105 = 3.5.7. Do đó An đúng.
Câu 5. Hãy phân tích A = 42.95 ra thừa số nguyên tố.
A. A = 42.95.
B. A = 24.95.
C. A = 42.310.
D. A = 24.310.
Đáp án: D
Giải thích:
Câu 6. Chọn câu sai:
A. 504 = 23.32.7.
B. 102 = 2.3.17.
C. 75 = 2.52.
D. 170 = 2.5.17.
Đáp án: C
Giải thích:
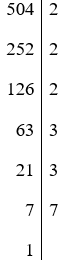
Vậy 504 = 23.32.7 nên A đúng.
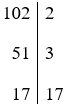
Vậy 102 = 2.3.17 nên B đúng
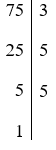
Vậy 75 = 3.52 nên C sai.
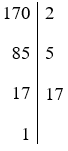
Vậy 170 = 2.5.17 nên D đúng.
Câu 7.Tìm các số còn thiếu trong sơ đồ phân tích một số ra thừa số nguyên tố sau:
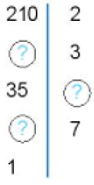
Các số cần điền từ lần lượt từ trên xuống dưới là:
A. 105; 5 và 7.
B. 105; 7 và 5.
C. 150; 5 và 7.
D. 150; 7 và 5.
Đáp án: A
Giải thích:
+) Ta có:
210 : 2 = 105
105 : 3 = 35
35 : 5 = 7
7 : 7 = 1
Ta hoàn thiện sơ đồ:
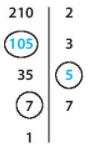
Vậy các số còn thiếu lần lượt từ trên xuống dưới là: 105; 5 và 7.
Câu 8. Tìm các số thích hợp điền vào ô trống trong sơ đồ sau:
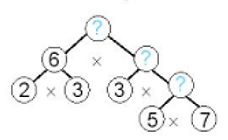
Các số cần điền lần lượt từ trên xuống dưới là:
A. 630; 35; 105.
B. 35; 105; 630.
C. 630; 105; 35.
D. 35; 630; 105.
Đáp án: B
Giải thích:
Ta có: 5 x 7 = 35;
35 x 3 = 105;
105 x 6 = 630.
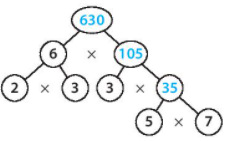
Vậy các số cần điền từ trên xuống dưới lần lượt là: 630; 105 và 35.
III. Vận dụng
Câu 1. Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau, số người trong một nhóm là các số nguyên tố. Hỏi có bao nhiêu cách chia?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
Phân tích 30 ra thừa số nguyên tố ta được: 30 = 2.3.5
Vì cô giáo muốn chia lớp 30 học sinh thành các nhóm, các nhóm có số người bằng nhau nên số người của mỗi ngóm là ước của 30.
Mà số người mỗi nhóm là số nguyên tố nên số người mỗi nhóm là ước nguyên tố của 30.
Ta có bảng sau:

Do đó có thể chia thành 15 nhóm, 10 nhóm hoặc 6 nhóm.
Câu 2. Trong nghi lễ thượng cờ lúc 6 giờ sáng và hạ cờ lúc 21 giờ hàng ngày ở Quảng trường Ba Đình, đội tiêu binh có 34 người gồm 1 sĩ quan chỉ huy đứng đầu và 33 chiến sĩ. Hỏi có bao nhiêu cách sắp xếp 33 chiến sĩ thành các hàng, sao cho mỗi hàng có số người như nhau?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: D
Giải thích:
Ta có: 33 = 3 . 11
Vì xếp 33 chiến sĩ thành các hàng thì số hàng là ước của 33
Ư(33) = {1; 3; 11; 33}
Với số hàng là 1 thì số người mỗi hàng là: 33 : 1 = 33 (người)
Với số hàng là 3 thì số người mỗi hàng là: 33 : 3 = 11 (người)
Với số hàng là 11 thì số người mỗi hàng là: 33 : 11 = 3 (người)
Với số hàng là 33 thì số người mỗi hàng là: 33 : 33 = 1 (người)
Vậy có 4 cách cách sắp xếp 33 chiến sĩ thành các hàng.
Câu 3. Hai số nguyên tố được gọi là sinh đôi nếu chúng hơn kém nhau hai đơn vị. Ví dụ 17 và 19 là hai số nguyên tố sinh đôi. Em hãy liệt kê các cặp số nguyên tố sinh đôi nhỏ hơn 40. Có tất cả bao nhiêu cặp?
A. 5;
B. 6;
C. 7;
D. 8.
Đáp án: A
Giải thích:
Các cặp số nguyên tố sinh đôi nhỏ hơn 40:
+) 3 và 5
+) 5 và 7
+) 11 và 13
+) 17 và 19
+) 29 và 31
Vậy có tất cả 5 cặp.
Câu 4. Có bao nhiêu cách để phân tích một số ra thừa số nguyên tố?
A. 1;
B. 3;
C. 2;
D. 4.
Đáp án: C
Câu 5. Khẳng định nào sau đây đúng?
A. A = {0; 1} là tập hợp số nguyên tố
B. A = {1; 3; 5} là tập hợp các hợp số.
C. A = {3; 5} là tập hợp số nguyên tố.
D. A = {7; 8} là tập hợp các hợp số.
Đáp án: C
Câu 6. Có bao nhiêu khẳng định đúng trong các khẳng định sau?
a) Ước nguyên tố của 18 là 1; 2; và 3.
b) Tích của hai số nguyên tố bất kì luôn là số lẻ.
c) Mọi số chẵn đều là hợp số.
A. 2;
B. 1;
C. 0;
D. 3.
Đáp án: C
Câu 7. Số tự nhiên có 2 chữ số khác nhau nhỏ nhất chia hết cho các số nguyên tố nhỏ hơn hoặc bằng 5 là:
A. 20
B. 30
C. 25
D. 35
Đáp án: B
Câu 8. Cho A là tập hợp các số nguyên tố nhỏ hơn 30. Chọn đáp án đúng.
A. 1 ∈ A;
B. 17 ∈ A
C. 29 ∉ A;
D. 2 ∉ A;
Đáp án: B
Câu 9. Phân tích một số ra thừa số nguyên tố là:
A. phân tích số đó thành tích của số nguyên tố với các hợp số.
B. Phân tích số đó thành tích của hai thừa số nguyên tố.
C. Phân tích số đó thành tích của các thừa số nguyên tố.
D. phân tích số đó thành tích của các số tự nhiên.
Đáp án: B
Câu 10. Trong các khẳng định sau, khẳng định nào sai?
A. Mọi số nguyên tố đều là số lẻ
B. Có hai số tự nhiên liên tiếp đều là số nguyên tố
C. Có ba số lẻ liên tiếp đều là số nguyên tố
D. Số 1 không là số nguyên tố
Đáp án: A
Câu 11. Hoàn thành phát biểu sau: “Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có …”:
A. ước là 1.
B. ước là chính nó.
C. hai ước là 1 và chính nó.
D. duy nhất một ước.
Đáp án: C
Câu 12. Trong các số tự nhiên cho sau, số có ước nhiều nhất là:
A. 1035
B. 496
C. 1464
D. 1517
Đáp án: C
Câu 13. Cho các số 21; 71; 77; 101. Chọn phát biểu đúng trong các phát biểu sau?
A. Số 21 là hợp số, các số còn lại là số nguyên tố.
B. Chỉ có một số nguyên tố, còn lại là hợp số.
C. Có hai số nguyên tố và hai số là hợp số trong các số trên.
D. Không có số nguyên tố nào trong các số trên
Đáp án: C
Các câu hỏi trắc nghiệm Toán lớp 6 sách Kết nối tri thức có đáp án, chọn lọc khác:
Xem thêm các chương trình khác:
- Trắc nghiệm Địa Lí lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Khoa học tự nhiên lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Toán lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Văn lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Địa Lí lớp 6 có đáp án – Cánh Diều
- Trắc nghiệm Toán lớp 6 có đáp án – Cánh Diều
- Trắc nghiệm Công nghệ lớp 6 có đáp án – Cánh Diều
- Trắc nghiệm Khoa học tự nhiên lớp 6 có đáp án – Cánh Diều
- Trắc nghiệm Văn lớp 6 có đáp án – Cánh Diều
- Trắc nghiệm Lịch sử lớp 6 có đáp án – Cánh Diều
