Toán 8 Bài 3 (Chân trời sáng tạo): Các trường hợp đồng dạng của hai tam giác vuông

Giải Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Giải Toán 8 trang 73 Tập 2

Khởi động trang 73 Toán 8 Tập 2: Bóng của một ngọn cờ trên mặt đất dài 6 m. Cùng thời điểm đó một thanh sắt cao 2,4 m cắm vuông góc với mặt đất có bóng dài 1,8 m. Tính chiều cao của cột cờ.

Lời giải:

Sau bài học này, ta giải quyết bài toán này như sau:

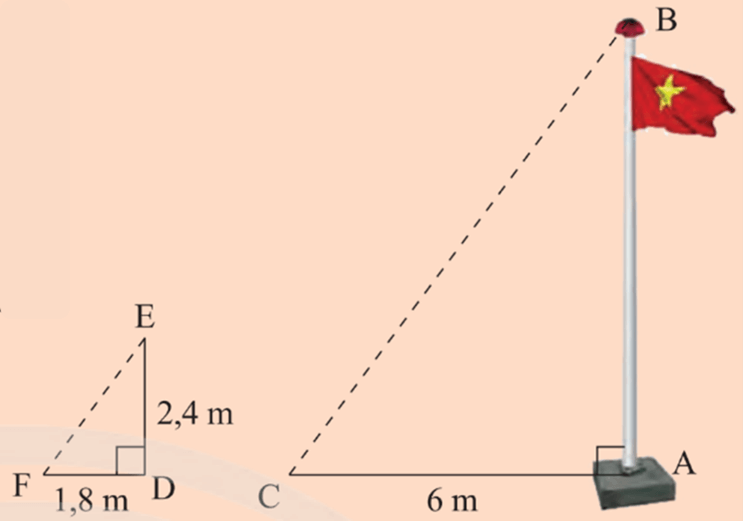
Theo hình vẽ, cột điện là AB, có bóng trên mặt đất là AC.

Thanh sắt là DE, có bóng trên mặt đất là DF.

Vì cột cờ và thanh sắt đều vuông góc với mặt đất nên hai ΔABC và ΔDEF đều là tam giác vuông.

Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau nên .

Xét ΔABC và ΔDEF có:

$\hat{\mathrm{B}}=\hat{\mathrm{E}}$

$\hat{\mathrm{A}}=\hat{\mathrm{D}}={90}^{\mathrm{o}}$

Do đó ΔABC ᔕ ΔDEF (g.g)

Suy ra: $\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}$ (các cạnh tương ứng).

Thay số: $\frac{\mathrm{AB}}{2,4}=\frac{6}{1,8}$ nên $\mathrm{AB}=\frac{2,4.6}{1,8}=8$ (m)

Vậy chiều cao cột cờ là 8 m.

1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông

Khám phá 1 trang 73 Toán 8 Tập 2: a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác ABC vuông tại A và tam giác MNP vuông tại M có $\hat{\mathrm{B}}=\hat{\mathrm{N}}$ thì hai tam giác đó có đồng dạng với nhau không?

b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác ABC vuông tại A và tam giác MNP vuông tại M có $\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{AC}}{\mathrm{MP}}$ thì tam giác đó có đồng dạng với nhau không.

Lời giải:

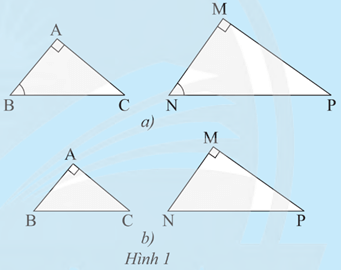
a) Xét tam giác ABC và tam giác MNP có:

$\hat{\mathrm{B}}=\hat{\mathrm{N}}$ (gt)

$\hat{\mathrm{A}}=\hat{\mathrm{M}}={90}^{\mathrm{o}}$

Do đó ΔABC ᔕ ΔMNP (g.g).

b) Xét tam giác ABC và tam giác MNP có:

$\hat{\mathrm{A}}=\hat{\mathrm{M}}={90}^{\mathrm{o}}$

$\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{AC}}{\mathrm{MP}}$

Do đó ΔABC ᔕ ΔMNP (c.g.c).

Giải Toán 8 trang 74 Tập 2

Thực hành 1 trang 74 Toán 8 Tập 2: Cho tam giác DEF vuông tại D có DH là đường cao (Hình 3). Chứng minh rằng ${\mathrm{DE}}^2$ = EH.EF.

Lời giải:

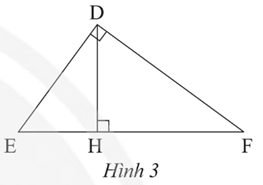
Tam giác HED vuông tại H và tam giác DEF vuông tại D có $\hat{\mathrm{E}}$ chung

Do đó ΔHED ᔕ ΔDEF (g.g)

Suy ra $\frac{\mathrm{EH}}{\mathrm{DE}}=\frac{\mathrm{DE}}{\mathrm{EF}}$ (các cạnh tương ứng).

Do đó DE² = EH.EF (đpcm).

Vận dụng 1 trang 74 Toán 8 Tập 2: Tính chiều cao của cột cờ trong Hoạt động khởi động (trang 73).

Lời giải:

Theo hình vẽ, cột điện là AB, có bóng trên mặt đất là AC.

Thanh sắt là DE, có bóng trên mặt đất là DF.

Vì cột cờ và thanh sắt đều vuông góc với mặt đất nên hai ΔABC và ΔDEF đều là tam giác vuông.

Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau nên $\hat{\mathrm{B}}=\hat{\mathrm{E}}$.

Xét ΔABC và ΔDEF có:

$\hat{\mathrm{B}}=\hat{\mathrm{E}}$

$\hat{\mathrm{A}}=\hat{\mathrm{D}}={90}^{\mathrm{o}}$

Do đó ΔABC ᔕ ΔDEF (g.g)

Suy ra: $\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}$ (các cạnh tương ứng).

Thay số: $\frac{\mathrm{AB}}{2,4}=\frac{6}{1,8}$ nên $\mathrm{AB}=\frac{2,4.6}{1,8}=8$(m)

Vậy chiều cao cột cờ là 8 m.

2. Thêm một dấu hiệu nhận biết hai tam giác vuông đồng dạng

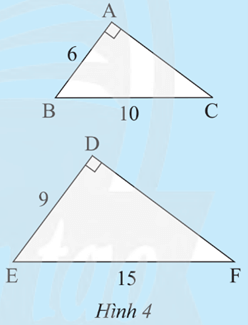
Khám phá 2 trang 74 Toán 8 Tập 2: Cho hai tam giác vuông ABC và DEF có các kích thước như Hình 4.

a) Hãy tính độ dài cạnh AC và DF.

b) So sánh các tỉ số $\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}$ và $\frac{\mathrm{BC}}{\mathrm{EF}}$.

c) Dự đoán sự đồng dạng của hai tam giác ABC và DEF.

Lời giải:

a) Áp dụng định lí Pythagore cho tam giác vuông ABC, ta có:

BC² = AB² + AC²

Suy ra AC² = BC² – AB² = 10² – 6² = 64

Do đó AC = 8.

Áp dụng định lí Pythagore cho tam giác vuông DEF, ta có:

EF² = DE² + DF²

Suy ra DF² = EF² – DE² = 15² – 9² = 144.

Do đó DF = 12.

b) Ta có: $\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{6}{9}=\frac{2}{3}, \frac{\mathrm{AC}}{\mathrm{DF}}=\frac{8}{12}=\frac{2}{3}, \frac{\mathrm{BC}}{\mathrm{EF}}=\frac{10}{15}=\frac{2}{3}$.

Suy ra $\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{EF}}$.

c) Xét ΔABC và ΔDEF có: $\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{EF}}$ (câu b).

Dự đoán: ΔABC ᔕ ΔDEF.

Giải Toán 8 trang 75 Tập 2

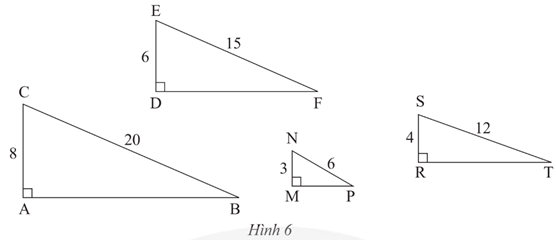
Thực hành 2 trang 75 Toán 8 Tập 2: Trong Hình 6, tam giác nào đồng dạng với tam giác DEF?

Lời giải:

• Tỉ số: $\frac{\mathrm{AC}}{\mathrm{DE}}=\frac{8}{6}=\frac{4}{3}; \frac{\mathrm{BC}}{\mathrm{FE}}=\frac{20}{15}=\frac{4}{3}$ .

Xét ΔABC và ΔDFE có:

$\frac{\mathrm{AC}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{FE}}=\frac{4}{3}$

Do đó ΔABC ᔕ ΔDFE (c.c.c).

• Tỉ số: $\frac{\mathrm{DE}}{\mathrm{MN}}=\frac{6}{3}=2;\frac{\mathrm{EF}}{\mathrm{NP}}=\frac{15}{6}=\frac{5}{2}$ .

Vì $\frac{\mathrm{DE}}{\mathrm{MN}}\ne \frac{\mathrm{EF}}{\mathrm{NP}}$ nên hai tam giác DEF và MNP không đồng dạng với nhau.

• Tỉ số: $\frac{\mathrm{DE}}{\mathrm{RS}}=\frac{6}{4}=\frac{3}{2};\frac{\mathrm{EF}}{\mathrm{ST}}=\frac{15}{12}=\frac{5}{4}$.

Vì nên hai tam giác DEF và RST không đồng dạng với nhau.

Vận dụng 2 trang 75 Toán 8 Tập 2: Trong Hình 7, biết ΔMNP ᔕ ΔABC với tỉ số đồng dạng $\mathrm{k}=\frac{\mathrm{MN}}{\mathrm{AB}}$, hai đường cao tương ứng là MK và AH.

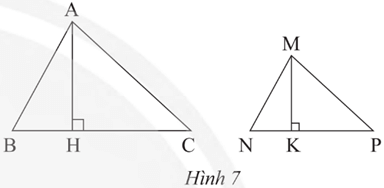
a) Chứng minh rằng ΔMNK ᔕ ΔABH và $\frac{\mathrm{MK}}{\mathrm{AH}}=\mathrm{k}$.

b) Gọi S1 là diện tích tam giác MNP và S2 là diện tích tam giác ABC. Chứng minh rằng $\frac{{\mathrm{S}}_1}{{\mathrm{S}}_2}={\mathrm{k}}^2$.

Lời giải:

a) Ta có ΔMNP ᔕ ΔABC nên $\hat{\mathrm{N}}=\hat{\mathrm{B}}$

Xét tam giác vuông MNK và ABH có $\hat{\mathrm{N}}=\hat{\mathrm{B}}$

Suy ra ΔMNK ᔕ ΔABH nên $\frac{\mathrm{MK}}{\mathrm{AH}}=\frac{\mathrm{MN}}{\mathrm{AB}}=\mathrm{k}$.

b) ΔMNP ᔕ ΔABC nên $\frac{\mathrm{NP}}{\mathrm{BC}}=\frac{\mathrm{MN}}{\mathrm{AB}}=\mathrm{k}$

Ta có ${\mathrm{S}}_1{\mathrm{S}}_2=\frac{{\displaystyle \frac{1}{2}}\mathrm{MK}.\mathrm{NP}}{{\displaystyle \frac{1}{2}}\mathrm{AH}.\mathrm{BC}}=\frac{\mathrm{MK}}{\mathrm{AH}}.\frac{\mathrm{NP}}{\mathrm{BC}}={\mathrm{k}}^2$.

Bài tập

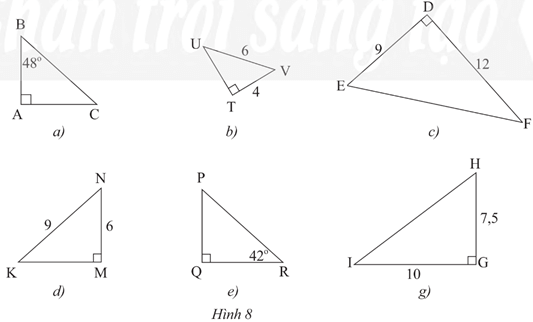
Bài 1 trang 75 Toán 8 Tập 2: Hãy tìm cặp tam giác vuông đồng dạng trong Hình 8.

Lời giải:

• Xét hai tam giác vuông TUV và MKN, ta có:

$\frac{\mathrm{UV}}{\mathrm{KN}}=\frac{\mathrm{TV}}{\mathrm{MN}}=\frac{2}{3}$

Suy ra ΔTUV ᔕ ΔMKN (c.g.c)

• Xét hai tam giác vuông DEF và GHI, ta có:

$\frac{\mathrm{DE}}{\mathrm{GH}}=\frac{\mathrm{DF}}{\mathrm{GI}}=\frac{6}{5}$

Suy ra ΔDEF ᔕ ΔGHI (c.g.c).

Tam giác PQR có $\stackrel{⏜}{\mathrm{P}}=90°-48°=42°$.

• Xét hai tam giác vuông BAC và PQR, ta có: $\hat{\mathrm{B}}=\hat{\mathrm{P}}=42°$

Suy ra ΔBAC ᔕ ΔPQR (g.g).

Giải Toán 8 trang 76 Tập 2

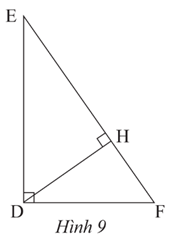
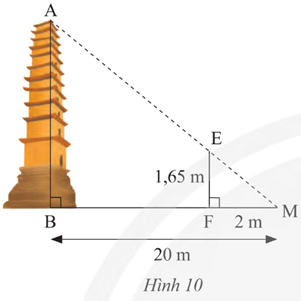
Bài 2 trang 76 Toán 8 Tập 2: Quan sát hình 9

a) Chứng minh rằng ΔDEF ᔕ ΔHDF.

b) Chứng minh DF² = FH.FE.

c) Biết EF = 15 cm, FH = 5,4 cm. Tính độ dài đoạn thẳng DF.

Lời giải:

a) Xét tam giác vuông DEF và HDE có: $\hat{\mathrm{E}}$ chung

Vậy ΔDEF ᔕ ΔHDF (g.g).

b) Từ câu b: ΔDEF ᔕ ΔHDF suy ra $\frac{\mathrm{DF}}{\mathrm{FH}}=\frac{\mathrm{FE}}{\mathrm{DF}}$ (các cạnh tương ứng).

Do đó DF² = FH.FE (đpcm).

c) Thay EF = 15 cm, FH = 5,4 cm ta có:

DF² = 5,4.15 = 81 suy ra DF = 9 cm.

Bài 3 trang 76 Toán 8 Tập 2: Trong Hình 10, biết MB = 20m, MF = 2m, EF = 1,65 m. Tính chiều cao AB của ngọn tháp.

Lời giải:

Xét ta giác vuông MEF và MAB ta có: $\hat{\mathrm{M}}$ chung

Suy ra ΔMEF ᔕ ΔMAB (g.g) nên $\frac{\mathrm{EF}}{\mathrm{AB}}=\frac{\mathrm{MF}}{\mathrm{MB}}$ (các cạnh tương ứng).

Khi đó $\frac{1,65}{\mathrm{AB}}=\frac{2}{20}$ suy ra $\mathrm{AB}=\frac{1,65.20}{2}=16,5$ (cm).

Vậy AB = 16,5 (cm).

Bài 4 trang 76 Toán 8 Tập 2: Trong Hình 11, cho biết $\hat{\mathrm{B}}=\hat{\mathrm{C}}$, BE = 25 cm, AB = 20 cm, DC = 15 cm. Tính độ dài đoạn thẳng CE.

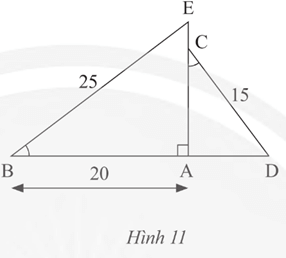
Lời giải:

Xét tam giác vuông ABE và ACD có $\hat{\mathrm{B}}=\hat{\mathrm{C}}$

Suy ra ΔABE ᔕ ΔACD (g.g) nên $\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BE}}{\mathrm{CD}}$ (các cạnh tương ứng).

Khi đó $\frac{20}{\mathrm{AC}}=\frac{25}{15}$ nên $\mathrm{AC}=\frac{20.15}{25}=12$(cm)

Vậy AC = 12 cm.

Áp dụng định lí Pythagore vào tam giác vuông ABE, ta có:

BE² = AB² + AE²

Suy ra $AE=\sqrt{B{E}^2-A{B}^2}=\sqrt{{25}^2-{20}^2}=15$ .

Do đó CE = AE – AC = 15 – 12 = 3 (cm).

Vậy CE = 3 cm.

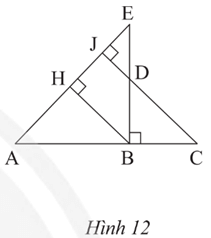
Bài 5 trang 76 Toán 8 Tập 2: Quan sát Hình 12. Chứng minh rằng:

a) ΔABH ᔕ ΔDCB.

b) $\frac{\mathrm{BC}}{\mathrm{BE}}=\frac{\mathrm{BD}}{\mathrm{BA}}$.

Lời giải:

a) Ta có BH ⊥ AE, CJ ⊥ AE nên BH // CJ.

Suy ra $\widehat{\mathrm{ABH}}=\widehat{\mathrm{BCD}}$ (hai góc so le trong)

Xét hai tam giác vuông ABH và DCB có:

$\widehat{\mathrm{ABH}}=\widehat{\mathrm{BCD}}$ (chứng minh trên).

Suy ra ΔABH ᔕ ΔDCB (g.g).

b) ΔABH ᔕ ΔDCB nên $\hat{\mathrm{A}}=\widehat{\mathrm{BDC}}$.

Xét tam giác vuông DCB và AEB ta có: $\hat{\mathrm{A}}=\widehat{\mathrm{BDC}}$ .

Suy ra ΔDCB ᔕ ΔAEB (g.g) nên $\frac{\mathrm{BC}}{\mathrm{BE}}=\frac{\mathrm{BD}}{\mathrm{BA}}$ (đpcm).

Bài 6 trang 76 Toán 8 Tập 2: Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3 m và đặt cách xa tòa nhà 27 m. Sau khi người ấy lùi ra xa cách cọc 1,2 m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng nằm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5 m.

Lời giải:

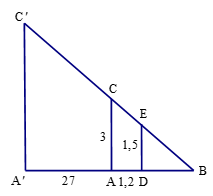
Gọi chiều cao của tòa nhà là h = A'C' và cọc tiêu AC = 3 m.

Khoảng cách từ chân đến mắt người đo là DE = 1,5 m.

Cọc xa cây một khoảng A'A = 27 m, và người cách cọc một khoảng AD = 1,2 m và gọi B là giao điểm của C'E và A'A.

Vì A'C' ⊥ A'B, AC ⊥ A'B, DE ⊥ A'B nên A'C' // AC // DE.

• ΔDEB ᔕ ΔACB (vì DE // AC)

Suy ra $\frac{\mathrm{DE}}{\mathrm{AC}}=\frac{\mathrm{DB}}{\mathrm{AB}}$ (các cặp cạnh tương ứng).

Mà AC = 3 m; DE = 1,5 m nên

$\frac{1,5}{3}=\frac{\mathrm{DB}}{\mathrm{AB}}\Rightarrow \frac{\mathrm{DB}}{\mathrm{AB}}=\frac{1}{2}\Rightarrow \frac{\mathrm{DB}}{1}=\frac{\mathrm{AB}}{2}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{\mathrm{DB}}{1}=\frac{\mathrm{AB}}{2}=\frac{\mathrm{AB}-\mathrm{DB}}{2-1}=\frac{\mathrm{AD}}{1}=1,2$

Suy ra $\frac{\mathrm{DB}}{1}=1,2$ nên DB = 1,2

$\frac{\mathrm{AB}}{2}=1,2$ suy ra AB = 2,4

Do đó A'B = A'A + AD + DB = 27 + 1,2 + 1,2 = 29,4 (m)

• ΔACB ᔕ ΔA'C'B (vì AC // A'C')

Suy ra $\frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{\mathrm{AC}}{\mathrm{A}\text{'}\mathrm{C}\text{'}}$ (các cặp cạnh tương ứng).

Do đó $\mathrm{A}\text{'}\mathrm{C}\text{'}=\frac{\mathrm{AC}.\mathrm{A}\text{'}\mathrm{B}}{\mathrm{AB}}=\frac{2.29,4}{2,4}=24,5$ (m)

Vậy tòa nhà cao 24,5 m.

Bài 7 trang 76 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HM vuông góc với AB tại M.

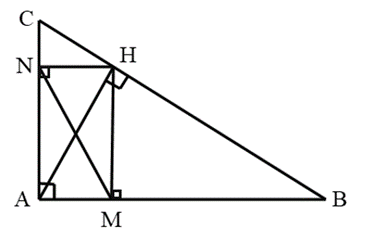
a) Chứng minh rằng ΔAMH ᔕ ΔAHB.

b) Kẻ HN vuông góc với AC tại N. Chứng minh rằng AM.AB = AN.AC.

c) Chứng minh rằng ΔANM ᔕ ΔABC.

d) Cho biết AB = 9 cm, AC = 12 cm. Tính diện tích tam giác AMH.

Lời giải:

a) Xét hai tam giác vuông AMH và AHB có: $\hat{\mathrm{A}}$ chung

Suy ra ΔAMH ᔕ ΔAHB (g.g)

b) ΔAMH ᔕ ΔAHB nên $\frac{\mathrm{AM}}{\mathrm{AH}}=\frac{\mathrm{AH}}{\mathrm{AB}}$ hay AM.AB = AH² (1)

Xét hai tam giác vuông ANH và AHC có: $\hat{\mathrm{A}}$ chung

Suy ra ΔANH ᔕ ΔAHC (g.g) nên $\frac{\mathrm{AN}}{\mathrm{AH}}=\frac{\mathrm{AH}}{\mathrm{AC}}$ hay AN.AC = AH² (2)

Từ (1) và (2) suy ra AM.AB = AN.AC (đpcm).

c) Ta có AM.AB = AN.AC, do đó $\frac{\mathrm{AN}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AC}}$.

Xét hai tam giác vuông AMN và ABC có:

$\frac{\mathrm{AN}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AC}}$ (chứng minh trên)

Do đó ΔANM ᔕ ΔABC (c.g.c)

d) Áp dụng định lí Pythagore vào tam giác ABC, ta có:

BC² = AB² + AC² = 9² + 12² = 225.

Suy ra BC = 15 cm.

Xét hai tam giác vuông ABC và HBA có $\hat{\mathrm{B}}$ chung

Do đó ΔABC ᔕ ΔHBA (g.g).

Suy ra $\frac{\mathrm{AC}}{\mathrm{AH}}=\frac{\mathrm{BC}}{\mathrm{AB}}$ (các cặp cạnh tương ứng).

Khi đó AH.BC = AB.AC hay AH.15 = 9.12.

Suy ra AH = 7,2 cm.

• Từ (1): AM.AB = AH² nên $\mathrm{AM}=\frac{{\mathrm{AH}}^2}{\mathrm{AB}}=\frac{7,2^2}{9}=5,76\left(\mathrm{cm}\right)$

• Từ (2): AN.AC = AH² nên $\mathrm{AN}=\frac{{\mathrm{AH}}^2}{\mathrm{AC}}=\frac{7,2^2}{12}=4,32\left(\mathrm{cm}\right)$

Diện tích tam giác AMN là:

$\frac{1}{2}.5,76.4,32=12,4416\left({\mathrm{cm}}^2\right)$.

Vậy diện tích tam giác AMN là 12,4416 cm².

Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông

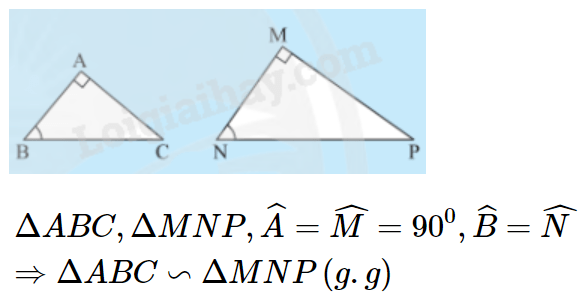
1. Trường hợp góc nhọn

Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

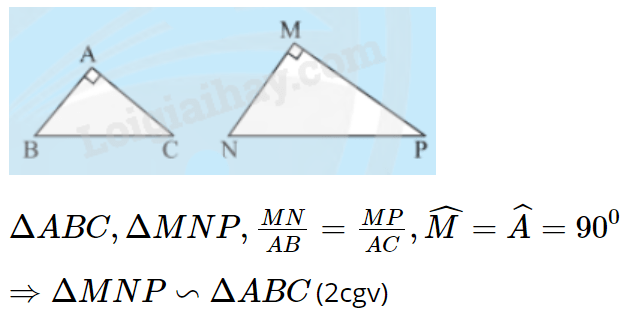
2. Trường hợp hai cạnh góc vuông

Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

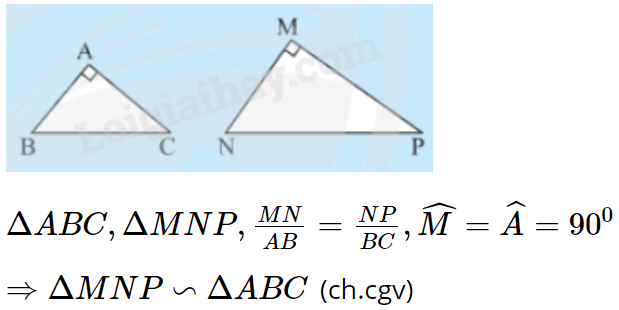
3. Trường hợp cạnh huyền cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng

Chú ý:

- Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.

- Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

Sơ đồ tư duy Các trường hợp đồng dạng của hai tam giác vuông

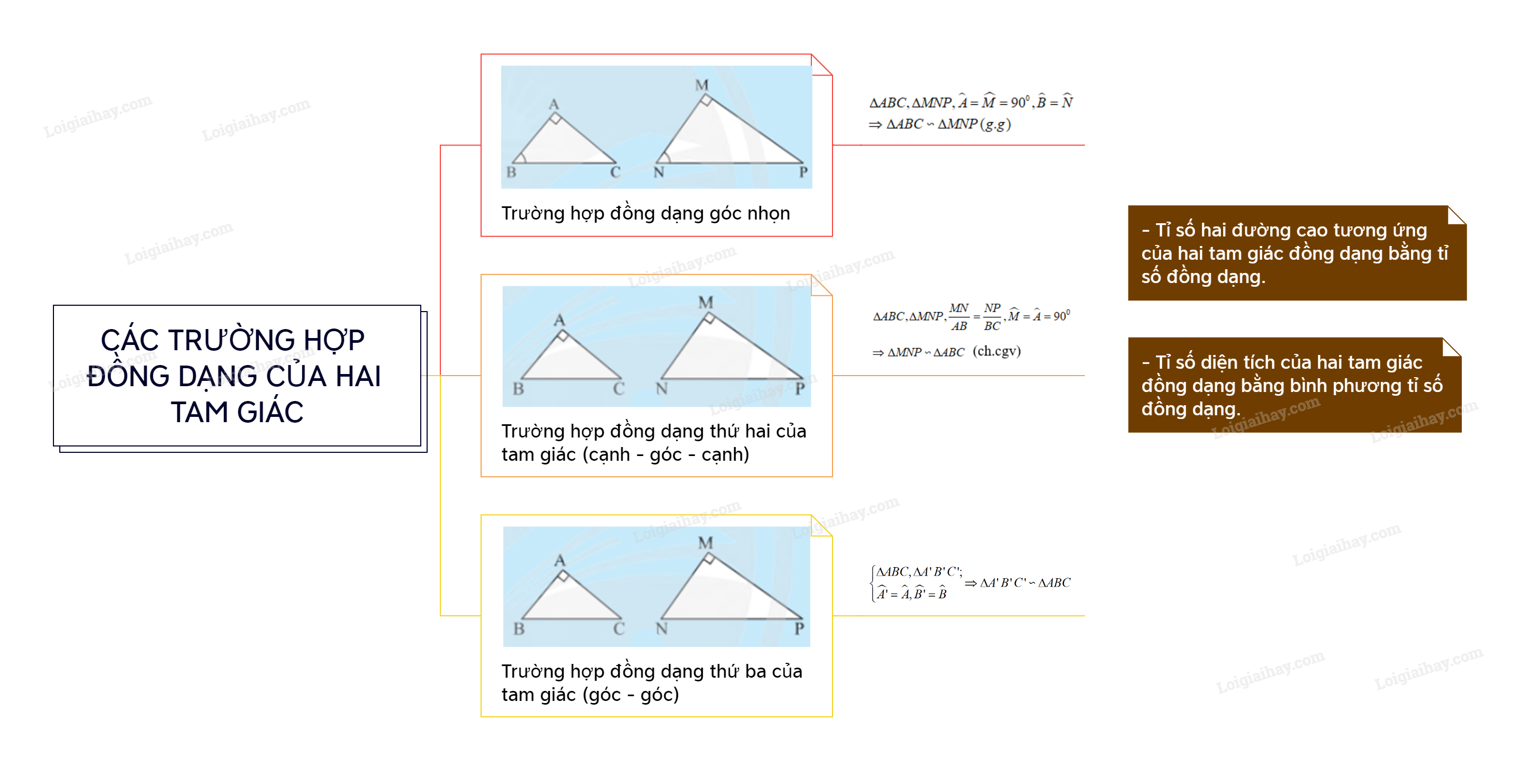
Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8 trang 84

Bài 1: Mô tả xác suất bằng tỉ số

Bài 2: Xác suất lí thuyết và xác suất thực nghiệm