Toán 8 (Chân trời sáng tạo): Bài tập cuối chương 8 trang 84

Giải Toán 8 Bài tập cuối chương 8 trang 84

Câu hỏi trắc nghiệm

Giải Toán 8 trang 84 Tập 2

Bài 1 trang 84 Toán 8 Tập 2: Trong các khẳng định sau, khẳng định nào đúng?

A. Hai tam giác đồng dạng thì bằng nhau.

B. Hai tam giác bằng nhau thì đồng dạng.

C. Hai tam giác bằng nhau thì không đồng dạng.

D. Hai tam giác cân thì luôn đồng dạng.

Lời giải:

Đáp án đúng là: B

Hai tam giác bằng nhau thì đồng dạng với theo tỉ số k = 1.

Bài 2 trang 84 Toán 8 Tập 2: Nếu ΔABC ᔕ ΔMNP theo tỉ số k = 3 thì ΔMNP ᔕ ΔABC theo tỉ số

A. $\frac{1}{3}$.

B. $\frac{1}{9}$.

C. 3.

D. 9.

Lời giải:

Đáp án đúng là: A

Ta có ΔABC ᔕ ΔMNP theo tỉ số k = 3.

Do đó ΔMNP ᔕ ΔABC theo tỉ số $\frac{1}{\mathrm{k}}=\frac{1}{3}$.

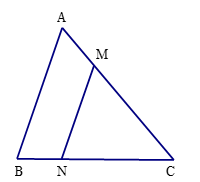
Bài 3 trang 84 Toán 8 Tập 2: Nếu tam giác ABC có MN // AB (với M ∈ AC, N ∈ BC) thì

A. ΔCMN ᔕ ΔABC.

B. ΔCNM ᔕ ΔCAB.

C. ΔCNM ᔕ ΔABC.

D. ΔMNC ᔕ ΔABC.

Lời giải:

Đáp án đúng là: D

Xét tam giác ABC có MN // AB nên ΔMNC ᔕ ΔABC.

Bài 4 trang 84 Toán 8 Tập 2: Cho ΔABD ᔕ ΔDEF với tỉ số đồng dạng $\mathrm{k}=\frac{1}{3}$ , biết AB = 9 cm. Khi đó DE bằng

A. 6 cm.

B. 12 cm.

C. 3 cm.

D. 27 cm.

Lời giải:

Đáp án đúng là: D

Ta có: ΔABD ᔕ ΔDEF nên $\frac{\mathrm{AB}}{\mathrm{DE}}=\mathrm{k}=\frac{1}{3}$ suy ra DE = 27 cm.

Bài 5 trang 84 Toán 8 Tập 2: Nếu tam giác ABC và tam giác EFG có $\hat{\mathrm{A}}=\hat{\mathrm{E}}, \hat{\mathrm{B}}=\hat{\mathrm{F}}$ thì

A. ΔABC ᔕ ΔEGF.

B. ΔABC ᔕ ΔEFG.

C. ΔACB ᔕ ΔGFE.

D. ΔCBA ᔕ ΔFGE.

Lời giải:

Đáp án đúng là: B

Xét ΔABC và ΔEFG có:

$\hat{\mathrm{A}}=\hat{\mathrm{E}}$

$\hat{\mathrm{B}}=\hat{\mathrm{F}}$

Do đó ΔABC ᔕ ΔEFG (g.g).

Bài 6 trang 84 Toán 8 Tập 2: Cho ΔXYZ ᔕ ΔEFG, biết XY = 6 cm; EF = 8 cm; EG = 12 cm. Khi đó XZ bằng

A. 10 cm.

B. 9 cm.

C. 12 cm.

D. 16 cm.

Lời giải:

Đáp án đúng là: B

Do ΔXYZ ᔕ ΔEFG nên $\frac{\mathrm{XY}}{\mathrm{EF}}=\frac{\mathrm{XZ}}{\mathrm{EG}}$.

Khi đó $\frac{6}{8}=\frac{\mathrm{XZ}}{12}$ nên XZ = 9 cm.

Bài 7 trang 84 Toán 8 Tập 2: Cho ΔABC ᔕ ΔDEF, biết $\hat{\mathrm{A}}={85}^{\mathrm{o}}, \hat{\mathrm{B}}={60}^0$. khi đó số đo $\hat{\mathrm{F}}$ bằng

A. 60°.

B. 85°.

C. 35°.

D. 45°.

Lời giải:

Đáp án đúng là: C

Ta có: ΔABC ᔕ ΔDEF nên

$\hat{\mathrm{A}}=\hat{\mathrm{D}}=85°, \hat{\mathrm{B}}=\hat{\mathrm{E}}=60°, \hat{\mathrm{C}}=\hat{\mathrm{F}}$

Do đó $\hat{\mathrm{F}}=180°-(85°+60°)=35°$ .

Bài 8 trang 84 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD), có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 8 cm, CD = 20 cm. Khi đó ΔAOB ᔕ ΔCOD với tỉ số đồng dạng là

A. $\mathrm{k}=\frac{2}{3}$ .

B. $\mathrm{k}=\frac{3}{2}$ .

C. $\mathrm{k}=\frac{2}{5}$ .

D. $\mathrm{k}=\frac{5}{2}$ .

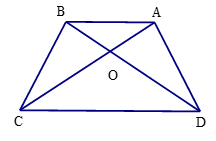
Lời giải:

Đáp án đúng là: C

Ta có ΔAOB ᔕ ΔCOD với tỉ số đồng dạng $\mathrm{k}=\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{8}{20}=\frac{2}{5}$.

Bài tập tư

Giải Toán 8 trang 85 Tập 2

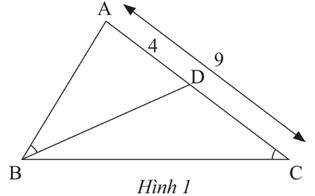
Bài 9 trang 85 Toán 8 Tập 2: Trong Hình 1, cho biết $\widehat{\mathrm{ABD}}=\widehat{\mathrm{ACB}}$, AC = 9 cm, AD = 4 cm.

a) Chứng minh tam giác ΔABD ᔕ ΔACB.

b) Tính độ dài cạnh AB.

Lời giải:

a) Xét ∆ABD và ∆ACB có:

$\hat{\mathrm{A}}$ chung

$\widehat{\mathrm{ABD}}=\widehat{\mathrm{ACB}}$

Do đó ΔABD ᔕ ΔACB (g.g).

b) Từ câu a: ΔABD ᔕ ΔACB nên $\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{AD}}{\mathrm{AB}}$

Khi đó AB² = AC.AD = 9.4 = 36

Do đó AB = 6 cm.

Bài 10 trang 85 Toán 8 Tập 2: a) Cho hình thang ABCD (AB // CD), biết $\widehat{\mathrm{ADB}}=\widehat{\mathrm{DCB}}$ (Hình 2a). Chứng minh rằng BD² = AB.CD.

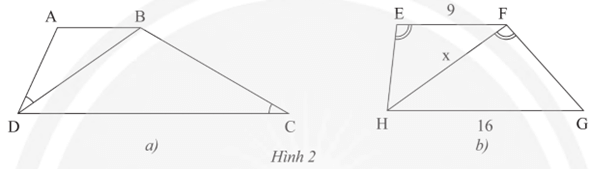
b) Cho hình thang EFGH (EF // GH), $\widehat{\mathrm{HEF}}=\widehat{\mathrm{HFG}}$ , EF = 9 m, GH = 16 m (Hình 2b). Tính độ dài x của HF.

Lời giải:

a) Xét ΔABD và ΔBDC có:

$\widehat{\mathrm{ADB}}=\widehat{\mathrm{DCB}}$ (gt)

$\widehat{\mathrm{ABD}}=\widehat{\mathrm{BDC}}$ (AB // CD, hai góc so le trong)

Do đso ΔABD ᔕ ΔBDC (g.g)

Suy ra $\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{BD}}{\mathrm{CD}}$ (các cạnh tương ứng).

Vậy BD² = AB.CD (đpcm).

b) Tương tự câu a, ta có: $\widehat{\mathrm{EHG}}=\widehat{\mathrm{FGH}}$

Xét tam giác EFH và FHG ta có:

$\widehat{\mathrm{EHG}}=\widehat{\mathrm{FGH}}$

$\widehat{\mathrm{HEF}}=\widehat{\mathrm{HFG}}$

Do đó ΔEFH ᔕ ΔFHG (g.g)

Suy ra $\frac{\mathrm{EF}}{\mathrm{HF}}=\frac{\mathrm{HF}}{\mathrm{GH}}$ (các cạnh tương ứng).

Khi đó HF² = EF.GH = 9.16 = 144 nên HF = 12 cm.

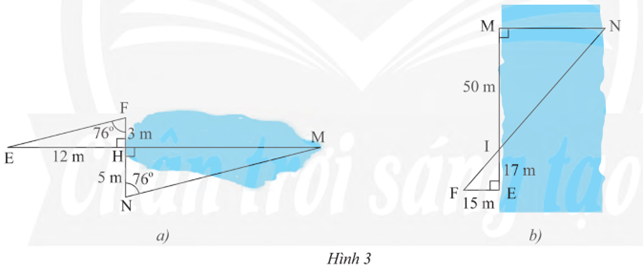
Bài 11 trang 85 Toán 8 Tập 2: a) Tính khoảng cách HM của mặt hồ ở Hình 3a.

b) Tính khoảng cách MN của một khúc sông ở Hình 3b.

Lời giải:

a) Xét hai tam giác vuông HEF và HMN ta có: $\hat{\mathrm{F}}=\hat{\mathrm{N}}={76}^{\mathrm{o}}$

Do đó ΔHEF ᔕ ΔHMN (g.g)

Nên $\frac{\mathrm{HE}}{\mathrm{HM}}=\frac{\mathrm{HF}}{\mathrm{HN}}$ suy ra $\mathrm{HM}=\frac{\mathrm{HE}.\mathrm{HN}}{\mathrm{HF}}=\frac{12.5}{3}=20\left(\mathrm{m}\right)$.

Vậy khoảng cách HM của mặt hồ ở Hình 3a là 20 m.

b) Xét hai tam giác vuông IMN và IEF có:

$\widehat{\mathrm{MIN}}=\widehat{\mathrm{EIF}}$ (đối đỉnh)

Do đó ΔIMN ᔕ ΔIEF (g.g)

Nên $\frac{\mathrm{MN}}{\mathrm{EF}}=\frac{\mathrm{IM}}{\mathrm{IE}}$ suy ra $\mathrm{MN}=\frac{\mathrm{EF}.\mathrm{IM}}{\mathrm{IE}}=\frac{15.50}{17}=\frac{750}{17}\left(\mathrm{m}\right)$ .

Vậy khoảng cách MN của một khúc sông ở Hình 3b là $\frac{750}{17}\mathrm{m}$ .

Bài 12 trang 85 Toán 8 Tập 2: Bóng của một căn nhà trên mặt đất có độ dài 6m. Cùng thời điểm đó, một cọc sắt cao 2m cắm vuông góc với mặt đất có bóng dài 1,5 m (Hình 4). Tính chiều cao ngôi nhà.

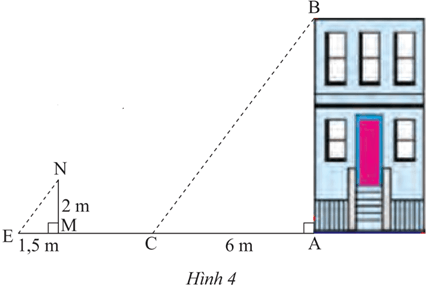
Lời giải:

Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau nên $\hat{\mathrm{C}}=\hat{\mathrm{E}}$.

Xét hai tam giác vuông ABC và tam giác MNE có: $\hat{\mathrm{C}}=\hat{\mathrm{E}}$

Do đó ΔABC ᔕ ΔMNE (g.g)

Suy ra: $\frac{\mathrm{AC}}{\mathrm{ME}}=\frac{\mathrm{AB}}{\mathrm{MN}}$

Thay số: $\frac{6}{1,5}=\frac{\mathrm{AB}}{2}$ suy ra AB = 8 (m)

Giải Toán 8 trang 86 Tập 2

Bài 13 trang 86 Toán 8 Tập 2: Người ta đo khoảng cách giữa hai điểm D và K ở hai bờ một dòng sông (Hình 5). Cho biết KE = 90 m, KF = 160 m. Tính khoảng cách DK.

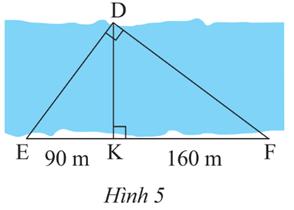
Lời giải:

Ta có $\widehat{\mathrm{EDK}}+\widehat{\mathrm{KDF}}=90°, \widehat{\mathrm{DFK}}+\widehat{\mathrm{KDF}}=90°$

Suy ra $\widehat{\mathrm{EDK}}=\widehat{\mathrm{DFK}}$.

Xét hai tam giác vuông DKE và FKD có:

$\widehat{\mathrm{EDK}}=\widehat{\mathrm{DFK}}$

Suy ra ΔDKE ᔕ ΔFKD (g.g)

Nên $\frac{\mathrm{KE}}{\mathrm{DK}}=\frac{\mathrm{DK}}{\mathrm{KF}}$ hay DK² = KE.KF

Do đó DK² = 90.160 =14 400 suy ra DK = 120 m.

Vậy khoảng cách DK bằng 120 m.

Bài 14 trang 86 Toán 8 Tập 2: Cho tam giác ABC nhọn có hai đường cao BE, CF cắt nhau tại H. Chứng minh rằng

a) ΔAEB ᔕ ΔAFC.

b) $\frac{\mathrm{HE}}{\mathrm{HC}}=\frac{\mathrm{HF}}{\mathrm{HB}}$.

c) ΔHEF ᔕ ΔHCB.

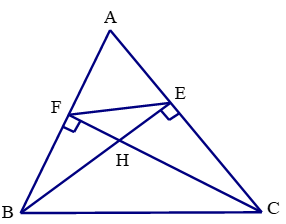
Lời giải:

a) Xét tam giác vuông AEB và AFC có:

$\hat{\mathrm{A}}$ chung

Suy ra ΔAEB ᔕ ΔAFC (g.g)

b) Xét tam giác vuông HCE và HBF ta có:

$\widehat{\mathrm{EHC}}=\widehat{\mathrm{FHB}}$ (hai góc đối đỉnh)

Suy ra ΔHCE ᔕ ΔHBF (g.g)

Nên $\frac{\mathrm{HE}}{\mathrm{HF}}=\frac{\mathrm{HC}}{\mathrm{HB}}$ hay $\frac{\mathrm{HE}}{\mathrm{HC}}=\frac{\mathrm{HF}}{\mathrm{HB}}$

c) Xét tam giác HEF và HCB ta có:

$\frac{\mathrm{HE}}{\mathrm{HC}}=\frac{\mathrm{HF}}{\mathrm{HB}}$ (cmt)

$\widehat{\mathrm{EHF}}=\widehat{\mathrm{BHC}}$ (hai góc đối đỉnh)

Suy ra ΔHEF ᔕ ΔHCB (c.g.c).

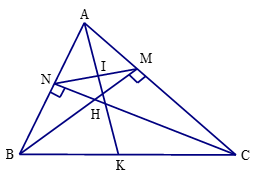
Bài 15 trang 86 Toán 8 Tập 2: Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H.

a) Chứng minh rằng ΔAMN ᔕ ΔABC.

b) Phân giác của $\widehat{\mathrm{BAC}}$ cắt MN và BC lần lượt tại I và K. Chứng minh rằng $\frac{\mathrm{IM}}{\mathrm{IN}}=\frac{\mathrm{KB}}{\mathrm{KC}}$.

Lời giải:

a) Xét tam giác vuông ABM và ACN có:

$\hat{\mathrm{A}}$ chung

Suy ra ΔABM ᔕ ΔACN (g.g)

Nên $\frac{\mathrm{AM}}{\mathrm{AN}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ hay $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$

Xét tam giác AMN và ABC ta có:

$\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$

$\hat{\mathrm{A}}$ chung

Suy ra ΔAMN ᔕ ΔABC (c.g.c).

b) ΔAMN ᔕ ΔABC, AK là phân giác của $\widehat{\mathrm{BAC}}$

Suy ra $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{AI}}{\mathrm{AK}}$

Xét tam giác AIM và AKB ta có:

$\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AK}}$

$\widehat{\mathrm{IAM}}=\widehat{\mathrm{IAN}}$ (vì AK là phân giác $\widehat{\mathrm{BAC}}$ )

Suy ra ΔAIM ᔕ ΔAKB nên $\frac{\mathrm{IM}}{\mathrm{KB}}=\frac{\mathrm{AI}}{\mathrm{AK}}$ (1)

Xét tam giác AIN và AKC ta có:

$\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{AI}}{\mathrm{AK}}$

$\widehat{\mathrm{IAM}}=\widehat{\mathrm{IAN}}$ (vì AK là phân giác $\widehat{\mathrm{BAC}}$ )

Suy ra ΔAIN ᔕ ΔAKC nên $\frac{\mathrm{IN}}{\mathrm{KC}}=\frac{\mathrm{AI}}{\mathrm{AK}}$ (2)

Từ (1) và (2) suy ra $\frac{\mathrm{IM}}{\mathrm{KB}}=\frac{\mathrm{IN}}{\mathrm{KC}}$ hay $\frac{\mathrm{IM}}{\mathrm{IN}}=\frac{\mathrm{KB}}{\mathrm{KC}}$.

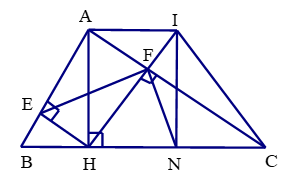
Bài 16 trang 86 Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H ∈ BC).

a) Chứng minh rằng ΔABH ᔕ ΔCBA, suy ra AB² = BH.BC.

b) Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F. Chứng minh rằng AE.AB = AF.AC.

c) Chứng minh rằng ΔAFE ᔕ ΔABC.

d) Qua A vẽ đường thẳng song song với BC cắt đường thẳng HF tại I. Vẽ IN vuông góc BC tại N. Chứng minh rằng ΔHNF ᔕ ΔHIC.

Lời giải:

a) Xét tam giác vuông ABH và CBA ta có:

$\hat{\mathrm{B}}$ chung

Suy ra ΔABH ᔕ ΔCBA nên $\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{BH}}{\mathrm{AB}}$ hay AB² = BH.BC

b) c) Tứ giác AEHF có 4 góc vuông suy ra AEHF là hình chữ nhật

Do đó $\widehat{\mathrm{AEF}}=\widehat{\mathrm{AEH}}$

ΔABH ᔕ ΔCBA nên $\widehat{\mathrm{ACB}}=\widehat{\mathrm{AEH}}$

Xét tam giác AEF và ACB ta có:

$\hat{\mathrm{A}}$ chung

$\widehat{\mathrm{ACB}}=\widehat{\mathrm{AEH}}$

Suy ra ΔAEF ᔕ ΔACB (g.g) nên $\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{\mathrm{AF}}{\mathrm{AB}}$ hay AE.AB = AF.AC

d) Xét tam giác vuông HNI và HFC ta có:

$\hat{\mathrm{H}}$ chung

Suy ra ΔHNI ᔕ ΔHFC (g.g)

Nên $\frac{\mathrm{HN}}{\mathrm{HF}}=\frac{\mathrm{HI}}{\mathrm{HC}}$ hay $\frac{\mathrm{HN}}{\mathrm{HI}}=\frac{\mathrm{HF}}{\mathrm{HC}}$

Xét tam giác HNF và HIC ta có:

$\hat{\mathrm{H}}$ chung

$\frac{\mathrm{HN}}{\mathrm{HI}}=\frac{\mathrm{HF}}{\mathrm{HC}}$

Suy ra ΔHNF ᔕ ΔHIC (c.g.c).

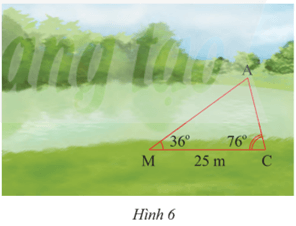
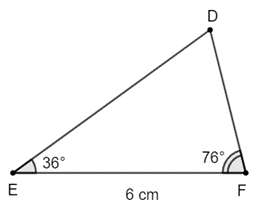
Bài 17 trang 86 Toán 8 Tập 2: Quan sát Hình 6. Vẽ vào tờ giấy tam giác DEF với EF = 4 cm, $\hat{\mathrm{E}}=36°, \hat{\mathrm{F}}=76°$ .

a) Chứng minh ΔDEF ᔕ ΔAMC.

b) Dùng thước đo chiều dài cạnh DF của ΔDEF. Tính khoảng cách giữa hai điểm A và C ở hai bờ sông trong Hình 6.

Lời giải:

a) Xét tam giác DEF và AMC có:

$\hat{\mathrm{E}}=\hat{\mathrm{M}}={36}^{\mathrm{o}}$

$\hat{\mathrm{F}}=\hat{\mathrm{C}}={76}^{\mathrm{o}}$

Suy ra ΔDEF ᔕ ΔAMC (g.g)

b) Đổi 25 m = 2500 cm.

Dùng thước đo độ dài cạnh DF ta được độ dài DF là 3,9 cm.

Vì ΔDEF ᔕ ΔAMC nên $\frac{\mathrm{EF}}{\mathrm{MC}}=\frac{\mathrm{DF}}{\mathrm{AC}}$ (hai cặp cạnh tương ứng có cùng tỉ lệ)

Thay số, $\mathrm{AC}=\frac{\mathrm{MC}.\mathrm{DF}}{\mathrm{EF}}=\frac{25.3,9}{0,05}=1625\left(\mathrm{m}\right)$

Vậy khoảng cách giữa hai điểm A và C là 1625 cm hay 16,25 m.

Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Hai hình đồng dạng

Bài 1: Mô tả xác suất bằng tỉ số

Bài 2: Xác suất lí thuyết và xác suất thực nghiệm

Bài tập cuối chương 9 trang 95

Hoạt động 4: Vẽ đồ thị hàm số bậc nhất y = ax + b bằng phần mềm