Nội dung bài viết

    Xem thêm

    Toán 8 Bài 1 (Chân trời sáng tạo): Khái niệm hàm số

    Với giải bài tập Toán lớp 8 Bài 1: Khái niệm hàm số sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 1.

    1 1,593 21/09/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Bài 1: Khái niệm hàm số

    Giải Toán 8 trang 6 Tập 2

    Khởi động trang 6 Toán 8 Tập 2: Số liệu về lượng mưa M (mm) trong 7 tháng mùa mưa của thành phố Đà Lạt năm 2020 được biểu diện theo số n chỉ tháng trong biểu đồ dưới đây.

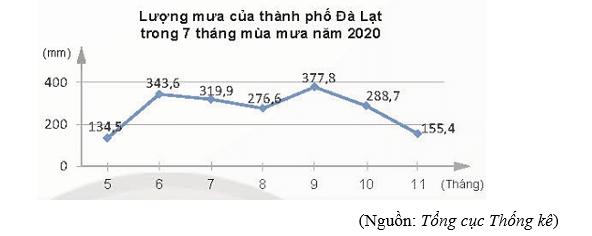
    Khởi động trang 6 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

    Quan sát biểu đồ và cho biết số lượng mưa ở mỗi tháng là bao nhiêu.

    Lời giải:

    Lượng mưa tháng 5 là 134,5 mm;

    Lượng mưa tháng 6 là 343,6 mm;

    Lượng mưa tháng 7 là 319,9 mm;

    Lượng mưa tháng 8 là 276,6 mm;

    Lượng mưa tháng 9 là 377,8 mm;

    Lượng mưa tháng 10 là 288,7 mm;

    Lượng mưa tháng 11 là 155,4 mm.

    1. Khái niệm hàm số

    Khám phá 1 trang 6 Toán 8 Tập 2: a) Nhiệt độ cơ thể d (°C) của bệnh nhân theo thời gian h (giờ) trong ngay được ghi trong bảng sau:

    h (giờ)

    7

    8

    9

    10

    11

    12

    13

    14

    15

    d (°C)

    36

    37

    36

    37

    38

    37

    38

    39

    39

    Ứng với mỗi giờ em đọc được bao nhiêu số chỉ nhiệt độ?

    b) Thời gian t (giờ) để một vật chuyển động đều đi hết quang đường 180 km tỉ lệ nghịch với vận tốc v (km/h) của nó theo công thức: t=180v .

    Tính và lập bảng các giá trị tương ứng của t khi v lần lượt bằng 10; 20; 30; 60; 180.

    Ứng với mỗi giá trị của đại lượng v em tính được bao nhiêu giá trị của đại lượng t?

    Lời giải:

    a) Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ.

    Ứng với 7h thì nhiệt độ là (36°C)

    Ứng với 8h thì nhiệt độ là (37°C)

    Ứng với 9h thì nhiệt độ là (36°C)

    Ứng với 10h thì nhiệt độ là (37°C)

    Ứng với 11h thì nhiệt độ là (38°C)

    Ứng với 12h thì nhiệt độ là (37°C)

    Ứng với 13h thì nhiệt độ là (38°C)

    Ứng với 14h thì nhiệt độ là (39°C)

    Ứng với 15h thì nhiệt độ là (39°C)

    b) Với v = 10 ⇒t=18010=18

    Với v = 20⇒t=18020=9

    Với v = 30⇒t=18030=6

    Với v = 60⇒t=18060=3

    Với v = 180⇒t=180180=1

    Ta có bảng:

    v

    10

    20

    30

    60

    180

    t

    18

    9

    6

    3

    1

    Giải Toán 8 trang 7 Tập 2

    Thực hành 1 trang 7 Toán 8 Tập 2: Mô tả các đại lượng là hàm số và biến số trong các mô hình sau:

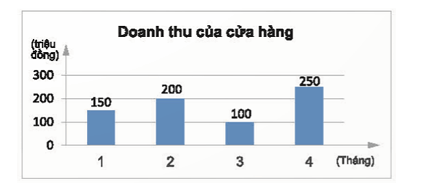
    a) Biểu đồ cột chỉ doanh thu y (triệu đồng) của một của hàng trong tháng x.

    Thực hành 1 trang 7 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

    b) Quãng đường s (km) đi được trong thời gian t (giờ) của một chiếc xe chạy với tốc độ không đổi bằng 40 km/h.

    c) Số tiền y (đồng) người mua phải trả cho x quyển vở có giá 10 000 đồng/quyển.

    Lời giải:

    a) Đại lượng là hàm số là doanh thu y (triệu đồng) của một cửa hàng và biến số là tháng x.

    b) Đại lượng là hàm số là quãng đường s (km) đi được và biến số là thời gian t (giờ).

    c) Đại lượng là hàm số là số tiền y (đồng) người mua phải trả và biến số là số x quyển vở.

    Vận dụng 1 trang 7 Toán 8 Tập 2: Khi đo nhiệt độ, ta có công thức đổi từ đơn vị độ C (Celsius) sang đơn vị độ F (Fahrenheit) như sau: F = 1,8C + 32. Theo em, F có phải là một hàm số theo biến số C hay không? Giải thích.

    Lời giải:

    F là một hàm số theo biến C vì với mỗi giá trị của C chỉ cho ta duy nhất một giá trị của F.

    2. Giá trị của hàm số

    Khám phá 2 trang 7 Toán 8 Tập 2: Cho biết đại lượng y được tính theo đại lượng x như sau: y = 2x + 3.

    x

    1

    2

    3

    4

    …

    y = 2x + 3

    5

    7

    9

    …

    …

    a) Tính y khi x = 4.

    b) Cho x một giá trị tùy ý, tính giá trị tương ứng của y.

    Lời giải:

    a) Với x = 4 ta có: y = 2.4 + 3 = 11

    b) Với x = 10 ta có: y = 10.4 + 3 = 43.

    Ta có bảng sau:

    x

    1

    2

    3

    4

    10

    y = 2x + 3

    5

    7

    9

    11

    43

    Giải Toán 8 trang 8 Tập 2

    Thực hành 2 trang 8 Toán 8 Tập 2: a) Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

    Đại lượng y có phải là hàm số của đại lượng x không?

    b) Cho hàm số y = f(x) = x2.

    - Tính f(2); f(−3).

    - Lập bảng giá trị của hàm số với x lần lượt bằng −3; −2; −1; 0; 1; 2; 3.

    Lời giải:

    a) Với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

    b) f(2) = 22 = 4; f(−3) = (−3)2 = 9.

    Ta có f(0) = 02 = 0; f(−1) = (−1)2 = 1;

    f(2) = 22 = 4; f(3) = 32 = 9.

    Từ đó ta có bảng:

    x

    −3

    −2

    −1

    0

    1

    2

    3

    y = x2

    9

    4

    1

    0

    1

    4

    9

    Vận dụng 2 trang 8 Toán 8 Tập 2: Gọi C = f(d) là hàm số mô tả mối quan hệ giữa chu vi C và đường kính d của một đường tròn. Tìm công thức f(d) và lập bảng giá trị của hàm số ứng với d lần lượt bằng 1; 2; 3; 4 (theo đơn vị cm).

    Lời giải:

    Ta có: C = πd trong đó, C là chu vi đường tròn; d là đường kính và π là số pi.

    Do đó, f(d) = π.d

    Với d = 1 ⇒ f(1) = π.1 = π

    d = 2 ⇒ f(2) = π.2 = 2π

    d = 3 ⇒ f(3) = π.3 = 3π

    d = 4 ⇒ f(4) = π.4 = 4π

    Ta thu được bảng sau:

    d

    1

    2

    3

    4

    f(d)

    π

    2π

    3π

    4π

    Bài tập

    Giải Toán 8 trang 9 Tập 2

    Bài 1 trang 9 Toán 8 Tập 2: Các giá trị tương ứng của hai đại lượng x và y được cho trong các bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng y có phải là hàm số của đại lượng x không.

    Giải thích.

    a)

    x

    0

    1

    2

    3

    4

    5

    6

    7

    y

    1

    2

    3

    4

    5

    6

    7

    8

    b)

    Bài 1 trang 9 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

    Lời giải:

    a) Dựa vào bảng, ta thấy với một giá trị của x ta chỉ nhận được một giá trị của y tương ứng, do đó đại lượng y là hàm số của đại lượng x.

    b) Dựa vào bảng, ta thấy tồn tại một giá trị của x ta có thể nhận được hai giá trị của y tương ứng, do đó đại lượng y không là hàm số của đại lượng x.

    Ví dụ: Khi x = 2 thì y = 12 hoặc y = 13 .

    Bài 2 trang 9 Toán 8 Tập 2: Cho hàm số y = f(x) = 3x.

    a) Tính f(1); f(−2); f13 .

    b) Lập bảng các giá trị tương ứng của y khi x lần lượt nhận các giá trị: −3; −2; −1; 0; 1; 2; 3.

    Lời giải:

    a) Ta có:

    • f(1) = 3.1 = 3;

    • f(−2) = 3.(−2) = −6;

    • f13=3.13=1 .

    b) Ta có f(−3) = 3.(−3) = −9; f(−1) = 3.(−1) = −3;

    f(0) = 3.0 = 0; f(2) = 3.2 = 6; f(3) = 3.3 = 9.

    Từ đó ta có bảng sau:

    x

    −3

    −2

    −1

    0

    1

    2

    3

    y = 3x

    −9

    −6

    −3

    0

    3

    6

    9

    Bài 3 trang 9 Toán 8 Tập 2: Cho hàm số y = f(x) = x2 + 4. Tính f(−3); f(−2); f(−1); f(0); f(1).

    Lời giải:

    • f(−3) = (−3)2 + 4 = 9 + 4 = 13;

    • f(−2) = (−2)2 + 4 = 4 + 4 = 8;

    • f(−1) = (−1)2 + 4 = 5;

    • f(0) = 0 + 4 = 4;

    • f(1) = 1 + 4 = 5.

    Vậy f(−3) = 13; f(−2) = 8; f(−1) = 5; f(0) = 4; f(1) = 5.

    Bài 4 trang 9 Toán 8 Tập 2: Khối lượng m (g) của một thanh sắt có khối lượng riêng là 7,8 kg/dm3 tỉ lệ thuận với thể tích V (cm3) theo công thức m = 7,8V. Đại lượng m có phải là hàm số của đại lượng V không? Nếu có, tính m(10); m(20); m(30); m(40); m(50).

    Lời giải:

    Đại lượng m là hàm số của đại lượng V vì với mỗi một giá trị của V ta luôn chỉ xác định được một giá trị của m.

    Ta có: m = 7,8V

    m(10) = 7,8.10 = 78;

    m(20) = 7,8.20 = 156;

    m(40) = 7,8.40 = 312;

    m(50) = 7,8.50 = 390.

    Bài 5 trang 9 Toán 8 Tập 2: Thời gian t(giờ) của một vật chuyển động đều trên quãng đương 20km tỉ lệ nghịch với tốc độ v (km/h) của nó theo công thức t=20v . Tính và lập bảng các giá trị tương ứng của t khi v lần lượt nhận các giá trị 10; 20; 40; 80.

    Lời giải:

    • Với v = 10 ta có t=2010=2 ;

    • Với v = 20 ta có t=2020=1 ;

    • Với v = 40 ta có t=2040=0,5 ;

    • Với v = 80 ta có t=2080=0,25 .

    Khi đó, ta có bảng sau:

    v (km/h)

    10

    20

    40

    80

    t (giờ)

    2

    1

    0,5

    0,25

    Lý thuyết Khái niệm hàm số

    1. Hàm số

    Khái niệm:

    Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

    Ví dụ: Ta có bảng nhiệt độ dự báo ở Thủ đô Hà Nội ngày 25/5/2023.

    t(h)

    10

    11

    12

    13

    T(0C)

    32

    33

    34

    34

    Ta có nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T.

    Ngược lại, thời điểm t không phải là hàm số của nhiệt độ T, vì nhiệt độ T = 340C tương ứng với hai thời điểm khác nhau t = 12 và t = 13.

    2. Giá trị của hàm số

    Cách cho một hàm số

    Hàm số có thể được cho bằng bảng, biểu đồ hoặc bằng công thức,...

    Nếu y là hàm số của x, ta viết

    Ví dụ: Cho hàm số y = x + 3, ta có thể viết y = f(x) = x + 3.

    Giá trị của hàm số

    Cho hàm số y = f(x), nếu ứng với x = a ta có y = f(a) thì f(a) được gọi là giá trị của hàm số y = f(x) tại x = a

    Bảng giá trị của hàm số y = f(x)

    x

    a

    b

    c

    ...

    ...

    y = f(x)

    f(a)

    f(b)

    f(c)

    ...

    ...

    Ví dụ: Cho hàm số y = f(x) = -2x + 1.

    a. Tính f(10); f(-10)

    b. Lập bảng giá trị của hàm số với x lần lượt bằng -2; -1; 0; 1; 2

    Giải

    a. f(10) = -2.10 + 1 = -20 + 1 = -19

    f(-10) = -2.(-10) + 1 = 20 + 1 = 21

    b. Bảng giá trị của hàm số với x lần lượt bằng -2; -1; 0; 1; 2 là:

    x

    -2

    -1

    0

    1

    2

    y = f(x) = -2x + 1

    5

    3

    1

    -1

    -3

    Sơ đồ tư duy Khái niệm hàm số

    Khái niệm hàm số (ảnh 1)

    Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

    Bài 2: Tọa độ của một điểm và đồ thị của hàm số

    Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)

    Bài 4: Hệ số góc của đường thẳng

    Bài tập cuối chương 5

    Bài 1: Phương trình bậc nhất một ẩn

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,593 21/09/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: