Toán 8 Bài 1 (Chân trời sáng tạo): Hình chóp tam giác đều – Hình chóp tứ giác đều

Giải Toán 8 Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều

Bài giảng Toán 8 Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều - Chân trời sáng tạo

Giải Toán 8 trang 43 Tập 1

Khởi động trang 43 Toán 8 Tập 1: Hãy cho biết các mặt bên của kim tự tháp và khối rubik ở bên dưới là các hình gì.

Lời giải:

Các mặt bên của kim tự tháp và khối rubik ở hình trên là các hình tam giác.

1. Hình chóp tam giác đều - Hình chóp tứ giác đều

Khám phá 1 trang 43 Toán 8 Tập 1: Quan sát các hình không gian trong Hình 1 và trả lời các câu hỏi sau:

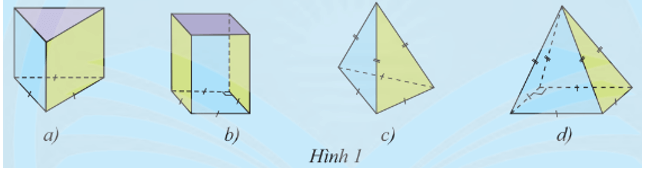
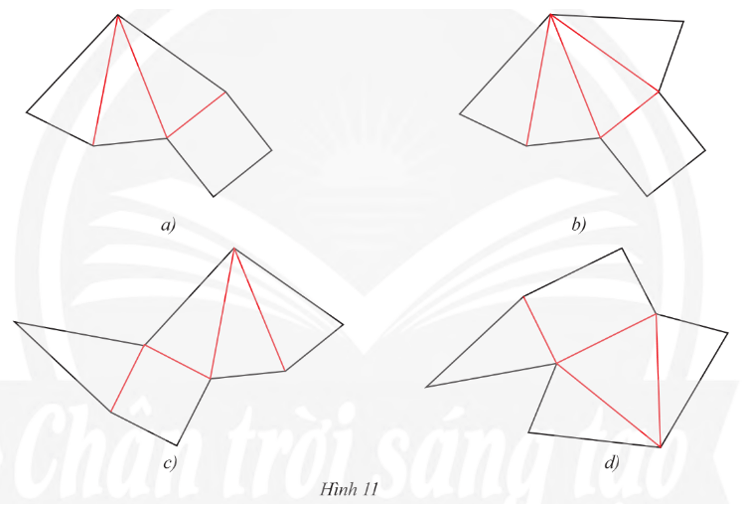
a) Các mặt bên của mỗi hình là hình gì?

b) Hình nào có các cạnh bên bằng nhau và đáy là hình tam giác đều?

c) Hình nào có các cạnh bên bằng nhau và đáy là hình vuông?

Lời giải:

a) Các mặt bên của Hình 1a, Hình 1b là hình chữ nhật.

Các mặt bên của Hình 1c, Hình 1d là hình tam giác.

b) Cả bốn hình (Hình 1a, 1b, 1c, 1d) đều có các cạnh bên bằng nhau.

Hình 1a và Hình 1c có đáy là tam giác đều.

Vậy Hình 1a và Hình 1c có các cạnh bên bằng nhau và đáy là hình tam giác đều.

c) Cả bốn hình (Hình 1a, 1b, 1c, 1d) đều có các cạnh bên bằng nhau.

Hình 1b và Hình 1d có đáy là hình vuông.

Vậy Hình 1b và Hình 1d có các cạnh bên bằng nhau và đáy là hình vuông.

Thực hành 1 trang 43 Toán 8 Tập 1: Hãy cho biết mặt bên, mặt đáy, đường cao, độ dài cạnh bên, độ dài cạnh đáy của hình chóp tam giác đều ở Hình 3.

Lời giải:

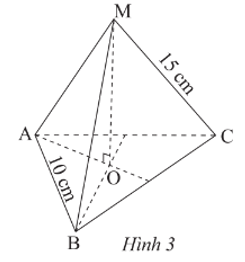
Hình chóp tam giác đều M.ABC ở Hình 3 có:

• Các mặt bên: MAB, MBC, MAC;

• Mặt đáy: ABC;

• Đường cao: MO;

• Độ dài cạnh bên: 15 cm (do các cạnh bên MA = MB = MC = 15 cm);

• Độ dài cạnh đáy: 10 cm (do các cạnh đáy AB = BC = CA = 10 cm).

Giải Toán 8 trang 44 Tập 1

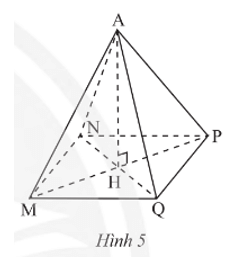
Thực hành 2 trang 44 Toán 8 Tập 1: Cho hình chóp tứ giác đều A.MNPQ (Hình 5).

a) Hãy cho biết đỉnh, cạnh bên, mặt bên, cạnh đáy, mặt đáy, đường cao của hình chóp tứ giác đều đó.

b) Cho biết AM = 5 cm, MN = 4 cm. Tìm độ dài các cạnh AN, AP, AQ, NP, PQ, QM.

Lời giải:

a) Hình chóp tứ giác đều A.MNPQ ở Hình 5 có:

• Đỉnh: A;

• Các cạnh bên: AM, AN, AP, AQ;

• Các mặt bên: AMN, ANP, APQ, AQM;

• Các cạnh đáy: MN, NP, PQ, QM;

• Mặt đáy: MNPQ;

• Đường cao: AH.

b) Cho biết AM = 5 cm, MN = 4 cm. Tìm độ dài các cạnh AN, AP, AQ, NP, PQ, QM.

Xét hình chóp tứ giác đều A.MNPQ có:

• AN = AP = AQ = AM = 5 cm;

• NP = PQ = QM = MN = 4 cm.

Vận dụng 1 trang 44 Toán 8 Tập 1: Chiếc hộp (Hình 6a) được vẽ lại như Hình 6b có dạng hình chóp tam giác đều S.MNP.

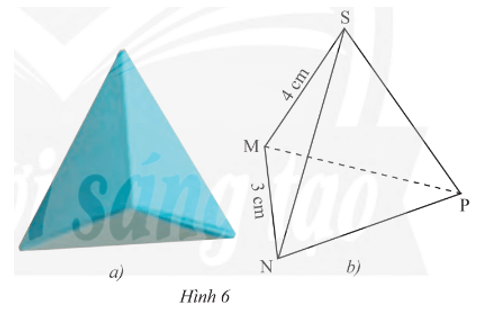
a) Hãy cho biết mặt đáy, mặt bên, cạnh bên của chiếc hộp đó.

b) Cho biết SM = 4 cm, MN = 3 cm. Tìm độ dài các cạnh còn lại của chiếc hộp.

c) Mỗi góc của tam giác đáy MNP bằng bao nhiêu độ?

Lời giải:

a) Chiếc hộp dạng hình chóp tam giác đều S.MNP ở Hình 6 có:

• Mặt đáy: MNP;

• Các mặt bên: SMN, SNP, SPM;

• Các cạnh bên: SM, SN, SP.

b) Xét chiếc hộp dạng hình chóp tam giác đều S.MNP có:

• SN = SP = SM = 4 cm;

• NP = PQ = MN = 3 cm.

c) Tam giác đáy MNP là tam giác đều nên mỗi góc của tam giác này bằng 60°.

2. Tạo lập hình chóp tam giác đều, hình chóp tứ giác đều

Thực hành 3 trang 44 Toán 8 Tập 1: Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3 cm và cạnh bên 4 cm theo hướng dẫn sau:

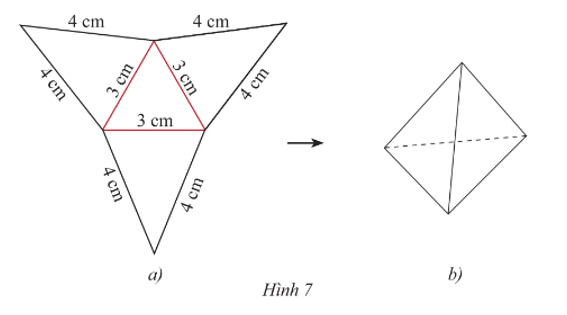
‒ Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.

‒ Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.

Lời giải:

Học sinh làm theo hướng dẫn để tạo lập hình chóp tam giác đều theo yêu cầu.

Gợi ý vẽ Hình 7a:

• Bước 1: Dùng thước thẳng và compa vẽ tam giác đều có cạnh 3 cm.

• Bước 2: Dùng thước thẳng và compa vẽ ra phía ngoài tam giác vừa vẽ ở Bước 1 các tam giác cân có độ dài cạnh bên là 4 cm, với các cạnh đáy lần lượt là cạnh của tam giác đều đã vẽ ở Bước 1.

Giải Toán 8 trang 45 Tập 1

Vận dụng 2 trang 45 Toán 8 Tập 1: Cắt, gấp và dán hộp quà hình chóp tam giác đều có độ dài cạnh đáy và cạnh bên bằng 5 cm.

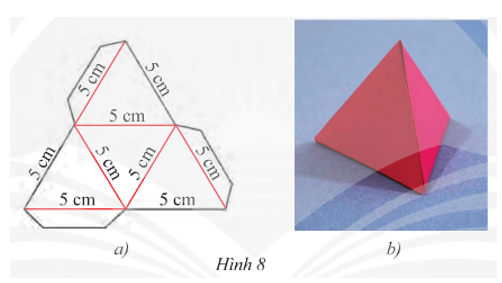
Gợi ý: Cắt theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.

Lời giải:

Học sinh làm theo hướng dẫn để tạo lập hình chóp tam giác đều theo yêu cầu.

Gợi ý vẽ Hình 8a:

• Bước 1: Dùng thước thẳng và compa vẽ tam giác đều có cạnh 5 cm.

• Bước 2: Dùng thước thẳng và compa vẽ ra phía ngoài tam giác vừa vẽ ở Bước 1 các tam giác đều có cạnh là 5 cm, có một cạnh là một trong ba cạnh của tam giác đều đã vẽ ở Bước 1.

• Bước 3: Vẽ thêm một phần mép bìa để gấp (dán) các mép hộp như Hình 8a.

Thực hành 4 trang 45 Toán 8 Tập 1: Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4 cm và cạnh bên 5 cm theo hướng dẫn sau:

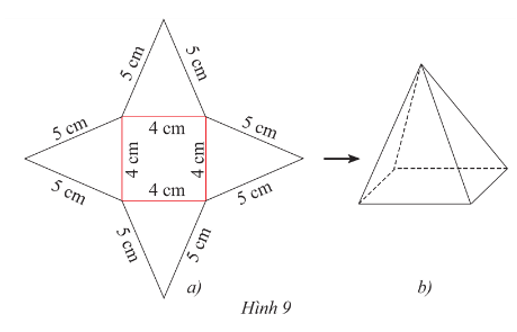
‒ Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.

‒ Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.

Lời giải:

Học sinh làm theo hướng dẫn để tạo lập hình chóp tứ giác đều theo yêu cầu.

Gợi ý vẽ Hình 9a:

• Bước 1: Dùng thước thẳng và êke vẽ hình vuông có cạnh 5 cm.

• Bước 2: Dùng thước thẳng và compa vẽ ra phía ngoài hình vuông vừa vẽ ở Bước 1 các tam giác cân có cạnh bên là 5 cm, với các cạnh đáy lần lượt là một trong bốn cạnh của hình vuông đã vẽ ở Bước 1.

Giải Toán 8 trang 46 Tập 1

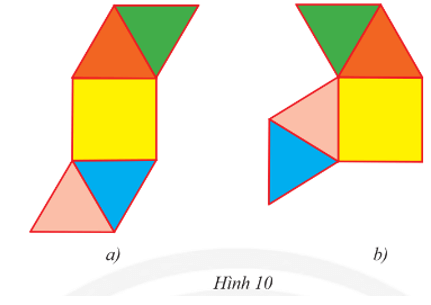
Vận dụng 3 trang 46 Toán 8 Tập 1: Tấm bìa nào sau đây có thể gấp thành hình chóp tứ giác đều?

Lời giải:

Tấm bìa Hình 10a có thể gấp thành hình chóp tứ giác đều.

Tấm bìa Hình 10b không thể gấp thành hình chóp tứ giác đều, vì khi gấp tạo lập hình chóp tứ giác đều thì tam giác màu xanh lá cây và tam giác màu hồng phải xếp chồng lên nhau, như vậy kết quả thiếu một mặt bên của hình chóp.

Bài tập

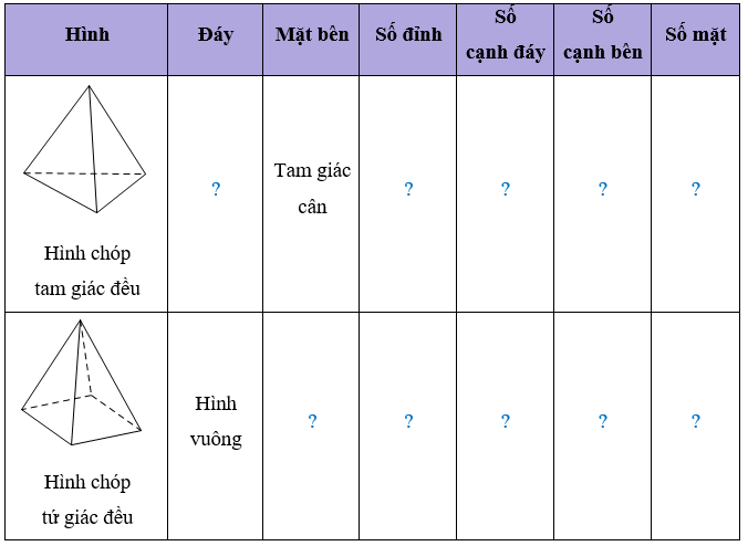
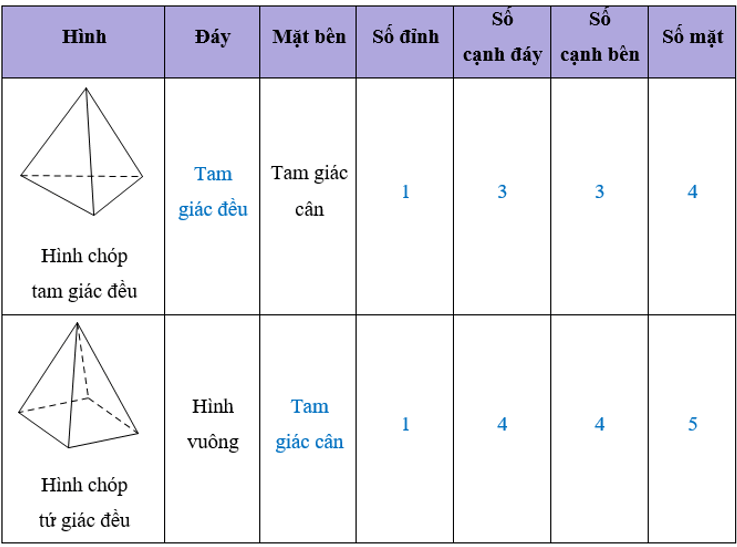
Bài 1 trang 46 Toán 8 Tập 1: Quan sát hai hình dưới đây và thay mỗi dấu ? cho thích hợp.

Lời giải:

Bài 2 trang 46 Toán 8 Tập 1: Cho hình chóp tứ giác đều S.MNPQ có cạnh bên SM = 15 cm và cạnh đáy MN = 8 cm. Hãy cho biết:

a) Mặt bên và mặt đáy của hình đó.

b) Độ dài các cạnh bên và cạnh đáy còn lại của hình đó.

Lời giải:

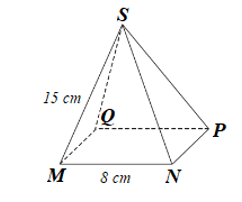
a) Hình chóp tứ giác đều S.MNPQ có:

• Mặt bên: SM, SN, SP, SQ;

• Mặt đáy: MNPQ.

b) Xét hình chóp tứ giác đều S.MNPQ có:

• SN = SP = SQ = SM = 15 cm;

• NP = PQ = QM = MN = 8 cm.

Giải Toán 8 trang 47 Tập 1

Bài 3 trang 47 Toán 8 Tập 1: Cho hình chóp tam giác đều S.DEF có cạnh bên SE = 5 cm và cạnh đáy EF = 3 cm. Hãy cho biết:

a) Mặt bên và mặt đáy của hình chóp.

b) Độ dài các cạnh bên và cạnh đáy còn lại của hình chóp.

c) Số đo mỗi góc của mặt đáy.

Lời giải:

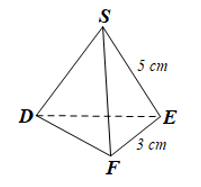
a) Hình chóp tam giác đều S.DEF có:

• Các mặt bên: SDE, SEF, SFD;

• Mặt đáy: DEF.

b) Hình chóp tam giác đều S.DEF có:

• SD = SF = SE = 5 cm;

• DE = DF = EF = 3 cm.

c) Mặt đáy của hình chóp S.DEF là tam giác đều DEF nên mỗi góc của tam giác này có số đo bằng 60°.

Vậy số đo mỗi góc của mặt đáy bằng 60°.

Bài 4 trang 47 Toán 8 Tập 1: Các phát biểu sau đúng hay sai? Nếu sai thì sửa lại cho đúng.

a) Hình chóp tam giác đều có các cạnh bên bằng nhau và đáy là hình tam giác có ba cạnh bằng nhau.

b) Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.

Lời giải:

a) Hình chóp tam giác đều có các cạnh bên bằng nhau và đáy là hình tam giác có ba cạnh bằng nhau. Phát biểu này là đúng.

b) Hình chóp tứ giác đều có tất cả các cạnh bằng nhau. Phát biểu này là sai.

Phát biểu đúng: Hình chóp tứ giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau.

Bài 5 trang 47 Toán 8 Tập 1: Trong các tấm bìa dưới đây, tấm bìa nào gấp theo đường màu đỏ thì được một hình chóp tứ giác đều?

Lời giải:

Tấm bìa Hình 11a có một mặt hình vuông, mặt này sẽ là mặt đáy của hình chóp tứ giác đều, tuy nhiên ta thấy chỉ có ba mặt hình tam giác cân, do đó thiếu một mặt bên nên tấm bìa này không gấp được hình chóp tứ giác đều.

Tấm bìa Hình 11b, Hình 11c tạo lập được hình chóp tứ giác đều.

Tấm bìa Hình 11d không có mặt nào có hình vuông nên không gấp được hình chóp tứ giác đều.

Bài 6 trang 47 Toán 8 Tập 1: Chị Hà dự định gấp một hộp quà từ tấm bìa như Hình 12. Cái hộp mà chị Hà dự định gấp có dạng hình gì?

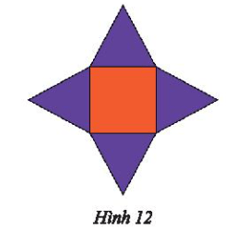
Lời giải:

Hộp quà mà chị Hà dự định gấp từ tấm bìa như Hình 12 có dạng hình chóp tứ giác đều.

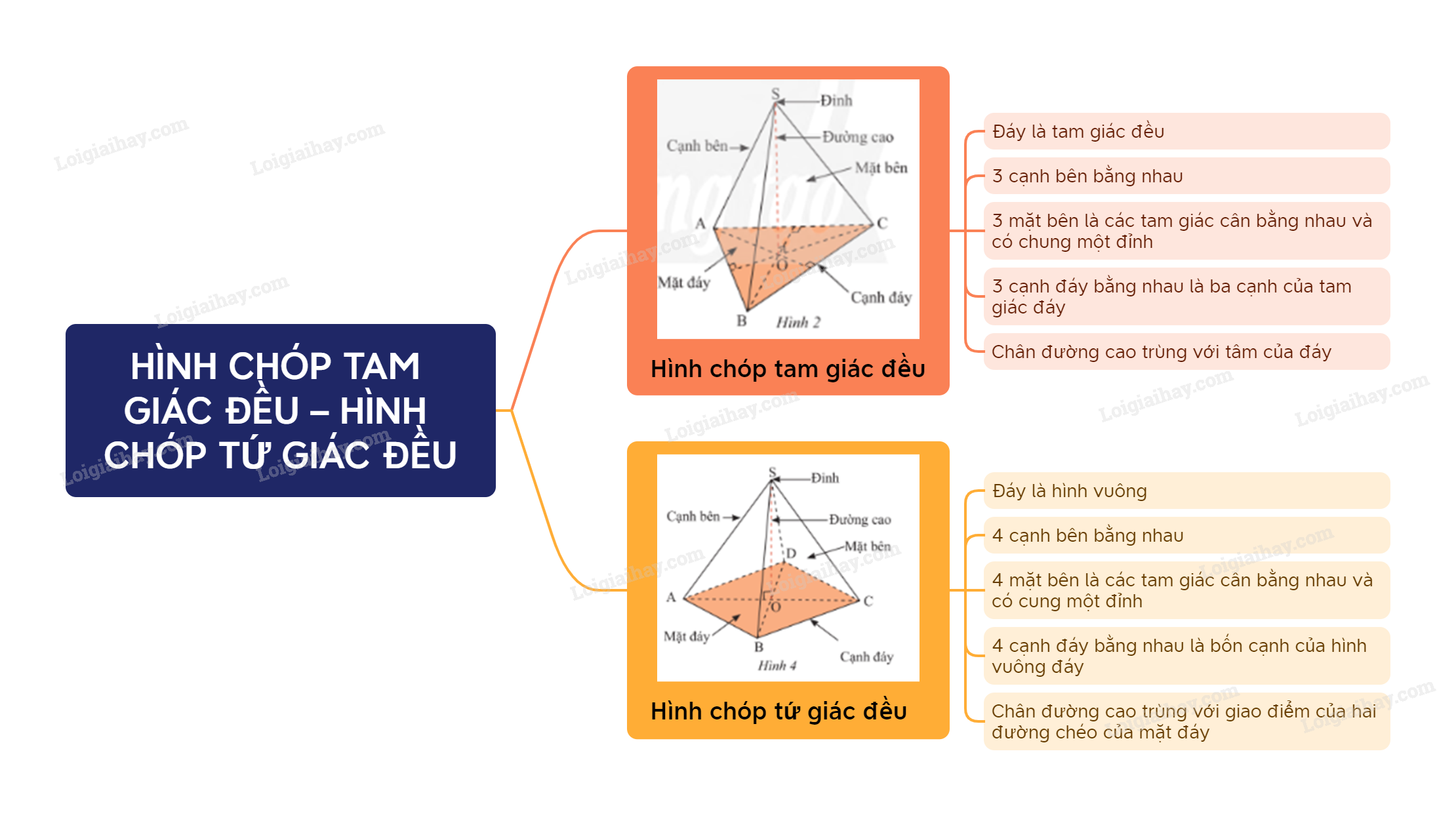
Lý thuyết Hình chóp tam giác đều – Hình chóp tứ giác đều

1. Hình chóp tam giác đều

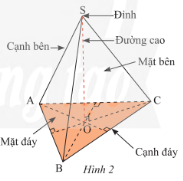
Hình chóp tam giác đều có:

- Đáy là tam giác đều.

- 3 cạnh bên bằng nhau.

- 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.

- 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.

- Chân đường cao trùng với tâm của đáy.

2. Hình chóp tứ giác đều

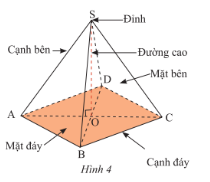
Hình chóp tứ giác đều có:

- Đáy là hình vuông.

- 4 cạnh bên bằng nhau.

- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.

- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.

- Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy.

Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Bài tập cuối chương 2

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân